Câu hỏi:
20/05/2022 310
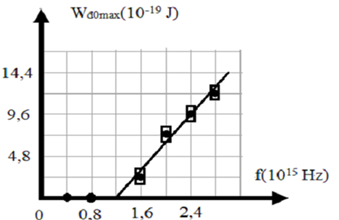
Người ta làm thí nghiệm khảo sát sự phụ thuộc động năng ban đầu cực đại của electron quang điện bay ra từ bề mặt catot vào tần số của ánh sáng kích thích. Sai số tuyệt đối của phép đo động năng ban đầu cực đại và tần số lần lượt là \({0,6.10^{ - 19}}J\) và \({0,05.10^{15}}Hz\). Kết quả đo thu được các điểm thực nghiệm như trên hình vẽ. Theo kết quả của thí nghiệm này thì hằng số Plăng có giá trị xấp xỉ bằng:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phương pháp giải:
+ Công thức Anh-xtanh: \[hf = A + {W_{d0\max }}\]
+ Sử dụng kĩ năng đọc và khai thác thông tin từ đồ thị.
Giải chi tiết:
Theo công thức Anh-xtanh về hiện tượng quang điện ta có:
\[hf = A + {W_{d0\max }} \Rightarrow {W_{d0\max }} = hf - A{\mkern 1mu} {\mkern 1mu} \left( * \right)\]
\[\left( * \right)\] có dạng \[y = a.x + b \Rightarrow \] Đồ thị động năng ban đầu cực đại \[{W_{d0max}}\] theo tần số f là đường thẳng.
Sai số của phép đo \[\left( {\Delta {W_{d0max}} = {{0,6.10}^{ - 19}}J;f = {{0,05.10}^{15}}Hz} \right)\] là các hình chữ nhật có tâm là các điểm thực nghiệm như hình vẽ.
Từ hình vẽ ta thấy:
+ Với \[\left\{ \begin{array}{l}f = {f_1} = {1,2.10^{15}}Hz\\{W_{d0max1}} = 0\end{array} \right. \Rightarrow 0 = h{.1,2.10^{15}} - A{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 1 \right)\]
+ Với \[\left\{ \begin{array}{l}f = {f_2} = {2,4.10^{15}}Hz\\{W_{d0max2}} = {9,6.10^{ - 19}}J\end{array} \right. \Rightarrow {9,6.10^{ - 19}} = h{.2,4.10^{15}} - A{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 2 \right)\]
Từ (1) và (2) ta có hệ phương trình: \[\left\{ \begin{array}{l}{1,2.10^{15}}.h - A = 0\\{2,4.10^{15}}.h - A = {9,6.10^{ - 19}}\end{array} \right. \Rightarrow h = {8.10^{ - 34}}\left( {J.s} \right)\].
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(\frac{{a\sqrt 6 }}{6}\)
Phương pháp giải:
- Gọi M là trung điểm của BC, trong (SOM) kẻ \(OH \bot SM{\mkern 1mu} {\mkern 1mu} \left( {H \in SM} \right)\), chứng minh \(OH \bot \left( {SBC} \right)\).
- Áp dụng định lí Pytago và hệ thức lượng trong tam giác vuông tính khoảng cách.
Giải chi tiết:
Gọi M là trung điểm của BC, suy ra OM là đường trung bình của tam giác ABC.
\( \Rightarrow OM\parallel AB\), mà \(AB \bot BC\)\( \Rightarrow OM \bot BC\) và \(OM = \frac{1}{2}AB = \frac{a}{2}\).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BC \bot OM}\\{BC \bot SO{\mkern 1mu} {\mkern 1mu} \left( {SO \bot \left( {ABCD} \right)} \right)}\end{array}} \right.\)\( \Rightarrow BC \bot \left( {SOM} \right)\)
Trong (SOM) kẻ \(OH \bot SM{\mkern 1mu} {\mkern 1mu} \left( {O \in SM} \right)\), ta có:
\(\left\{ {\begin{array}{*{20}{l}}{BC \bot \left( {SOM} \right) \Rightarrow BC \bot OH}\\{OH \bot SM}\end{array}} \right.\)\( \Rightarrow OH \bot \left( {SBC} \right)\)
\( \Rightarrow d\left( {O;\left( {SBC} \right)} \right) = OH\).
Tam giác SBC đều cạnh a nên \(SM = \frac{{a\sqrt 3 }}{2}\).
Áp dụng định lí Pytago trong tam giác vuông SOM có: .
Áp dụng hệ thức lượng trong tam giác vuông SOM có: \(OH = \frac{{SO.OM}}{{SM}} = \frac{{\frac{a}{{\sqrt 2 }}.\frac{a}{2}}}{{\frac{{a\sqrt 3 }}{2}}} = \frac{{a\sqrt 6 }}{6}\).
Vậy \(d\left( {O;\left( {SBC} \right)} \right) = \frac{{a\sqrt 6 }}{6}\).
Lời giải
Phương pháp giải:
CSC \(\left( {{u_n}} \right)\)có tổng \(n\) số hạng đầu: \({S_n} = {u_1} + {u_2} + ... + {u_n} = \frac{{n\left( {{u_1} + {u_n}} \right)}}{2}\)
Giải chi tiết:
Tổng số viên gạch: \(S = 1 + 2 + ... + 500 = \frac{{500.\left( {1 + 500} \right)}}{2} = 125250\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận