Câu hỏi:
22/05/2022 2,191
Cho hàm số với m là tham số. Hỏi có bao nhiêu giá trị nguyên của m lớn hơn \[ - 10\] để hàm số đã cho nghịch biến trên khoảng \[\left( { - \infty ;0} \right)\]?
Đáp án chính xác
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phương pháp giải: - Tìm đạo hàm của hàm số.
- Cô lập m, đưa bất phương trình về dạng \[m \le f(x)\forall x \in (a;b) \Leftrightarrow m \le \mathop {min}\limits_{[a;b]} f(x)\].
- Lập BBT của hàm số \[f(x)\] và kết luận.
Giải chi tiết:
Ta có hàm số nghịch biến trên khoảng khi
\[ \Leftrightarrow 4m \le 3{x^2} - 2x - 9\left( * \right)\]
Đặt \[f\left( x \right) = 3{x^2} - 2x - 9\]\[ \Rightarrow f'\left( x \right) = 6x - 2 = 0 \Leftrightarrow x = \frac{1}{3}\]
Bảng biến thiên:
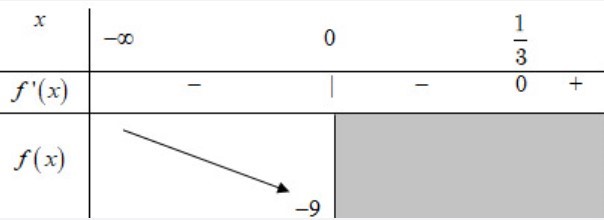
Dựa vào bảng biến thiên ta thấy bất phương trình (*) xảy ra khi
Kết hợp điều kiện nên . Mà .
Vậy có 7 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn B.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá từ mét khoản đầu tiên là 100000 đồng và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm 30000 đồng so với giá của mét khoan ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan giếng này để khoan một giếng sâu 20 mét lấy nước dùng cho sinh hoạt của gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán cho cơ sở khoan giếng số tiền bằng bao nhiêu?
Xem đáp án »
22/05/2022
30,574
Câu 2:
Lý luận giải phóng dân tộc của Nguyễn Ái Quốc được truyền bá vào Việt Nam trong những năm 1921 - 1929 có điểm khác biệt nào sau đây so với chủ trương cứu nước của các sĩ phu đầu thế kỉ XX?
Xem đáp án »
22/05/2022
28,515
Câu 3:
Cho tứ diện ABCD có M, N theo thứ tự là trung điểm của AB, BC. Gọi P là điểm thuộc cạnh CD sao cho \[CP = 2PD\]và Q là điểm thuộc cạnh AD sao cho bốn điểm M, N, P, Q đồng phẳng. Khẳng định nào sau đây là đúng?
Xem đáp án »
22/05/2022
14,587
Câu 4:
Một hộp chứa 10 quả cầu được đánh số theo thứ tự từ 1 đến 10, lấy ngẫu nhiên 5 quả cầu. Xác suất để tích các số ghi trên 5 quả cầu đó chia hết cho 3 bằng:
Xem đáp án »
23/05/2022
9,861
Câu 5:
Trong không gian Oxyz, cho ba điểm \[A(4;1;3),B(2;1;5),\,C(4;3; - 3)\] không thẳng hàng. Mặt phẳng đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với AB có phương trình là
Xem đáp án »
24/05/2022
9,214
Câu 7:
Trong điều trị bệnh ung thư, bệnh nhân được chiếu xạ với một liều xác định nào đó từ một nguồn phóng xạ. Biết nguồn có chu kỳ bán rã là 4 năm. Khi nguồn được sử dụng lần đầu thì thời gian cho 1 liều xạ là 10 phút. Hỏi sau hai năm thời gian cho 1 liều xạ là bao nhiêu phút:
Xem đáp án »
22/05/2022
6,007
Bình luận
🔥 Đề thi HOT:
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Top 5 đề thi Đánh giá năng lực trường ĐHQG Hà Nội có đáp án (Đề 1)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Nghĩa của từ
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 13)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Câu hỏi điền từ
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 2)
về câu hỏi!