Câu hỏi:

24/05/2022 425

Cho khối nón (N) đỉnh S, có chiều cao là $a\sqrt 3 $ và độ dài đường sinh là 3a. Mặt phẳng (P) đi qua đỉnh S, cắt và tạo với mặt đáy một khối nón một góc $60^\circ $. Tính diện tích thiết diện tạo bởi mặt phẳng (P) và khối nón (N).

A. $2{{\rm{a}}^2}\sqrt 5 $

B. ${a^2}\sqrt 3 $

C. $2{{\rm{a}}^2}\sqrt 3 $

D. ${a^2}\sqrt 5 $

Xem lời giải

Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án A

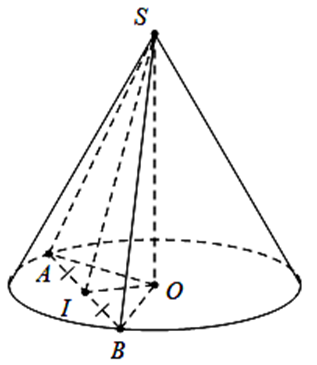
Cho khối nón (N) đỉnh S, có chiều cao là a căn bậc hai của 3 và độ dài đường sinh là 3a (ảnh 1)

Khối nón (N) có tâm đáy là O, chiều cao $SO = h = a\sqrt 3 $ và độ dài đường sinh $\ell = 3{\rm{a}}$.

Giả sử mặt phẳng (P) cắt (N) theo thiết diện là tam giác SAB.

Do $SA = SB = \ell \Rightarrow \Delta SAB$ cân tại đỉnh S.

Gọi I là trung điểm của AB. Ta có: $OI \bot AB,SI \bot AB$ và khi đó góc giữa mặt phẳng (P) và mặt đáy (N) là góc $\widehat {SI{\rm{O}}} = 60^\circ $.

Trong tam giác SOI vuông tại O góc $\widehat {SI{\rm{O}}} = 60^\circ $.

Ta có: $SI = \frac{{SO}}{{\sin SIO}} = \frac{{a\sqrt 3 }}{{\sin 60^\circ }} = 2a$.

Trong tam giác SIA ta có: $I{A^2} = S{A^2} - S{I^2} = 5{{\rm{a}}^2} \Rightarrow IA = a\sqrt 5 $.

$AB = 2IA = 2{\rm{a}}\sqrt 5 $. Vậy diện tích thiết diện cần tìm là:

${S_{t{\rm{d}}}} = {S_{SAB}} = \frac{1}{2}SI.AB = 2{{\rm{a}}^2}\sqrt 5 $.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian với hệ tọa độ Oxyz, cho các điểm $A\left( {1;0;3} \right),B\left( {2;3; - 4} \right),C\left( { - 3;1;2} \right)$. Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.

A. $D\left( { - 4; - 2;9} \right)$

B. $D\left( { - 4;2;9} \right)$

C. $D\left( {4; - 2;9} \right)$

D. $D\left( {4;2; - 9} \right)$

Lời giải

Đáp án A

Xét $D (x; y; z) \Rightarrow \vec{A D} = \vec{B C} \Leftrightarrow \{\begin{cases} x - 1 = - 5 \\ y = - 2 \\ z - 3 = 6 \end{cases} \Rightarrow D (- 4; - 2; 9)$

Câu 2

Cho \ $\int_{0}^{2} f (x) d x = 3$ và $\int_{0}^{2} g (x) d x = 7$ , khi đó $\int_{0}^{2} [f (x) + 3 g (x)] d x$ bằng

A. 16

B. $ - 18$

C. 24

D. 10

Lời giải

Đáp án C

Ta có $I = \int_{0}^{2} f (x) d x + 3 \int_{0}^{2} g (x) d x = 3 + 3.7 = 24$

Câu 3

Trong không gian với hệ tộa độ Oxyz, cho hai điểm $A\left( {0;1; - 2} \right)$ và $B\left( {3; - 1;1} \right)$. Tìm tọa độ của điểm M sao cho $\vec{A M} = 3 \vec{A B}$

A. $M\left( {9; - 5;7} \right)$

B. $M\left( {9;5;7} \right)$

C. $M\left( { - 9;5; - 7} \right)$

D. $M\left( {9; - 5; - 5} \right)$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Số nghiệm của phương trình ${\log _2}x = 3 - 2{\log _2}\left( {x - 4} \right)$ là

A. 1

B. 2

C. 3

D. 0

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hàm số \[y = f\left( x \right)\] có đạo hàm, nhận giá trị dương trên $\left( {0; + \infty } \right)$ và thỏa mãn $2f'\left( {{x^2}} \right) = 9{\rm{x}}\sqrt {f\left( {{x^2}} \right)} $ với mọi $x \in \left( {0; + \infty } \right)$. Biết $f\left( {\frac{2}{3}} \right) = \frac{2}{3}$, tính giá trị $f\left( {\frac{1}{3}} \right)$.

A. $\frac{1}{4}$

B. $\frac{1}{3}$

C. $\frac{1}{{12}}$

D. $\frac{1}{6}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong không gian Oxyz, cho hai điểm $A\left( { - 2;2; - 2} \right)$ và $B\left( {3; - 3;3} \right)$. Lấy M là điểm thay đổi luôn thỏa mãn $\frac{{MA}}{{MB}} = \frac{2}{3}$. Giá trị lớn nhất của độ dài đoạn OM bằng

A. $\frac{{5\sqrt 3 }}{2}$

B. $5\sqrt 3 $

C. $6\sqrt 3 $

D. $12\sqrt 3 $

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hàm số $f\left( x \right) = \ln \left( {{x^4} + 1} \right)$. Đạo hàm $f'\left( 1 \right)$ bằng

A. $\frac{1}{2}$

B. 1

C. $\frac{{\ln 2}}{2}$

D. 2

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Trong không gian với hệ tọa độ Oxyz, cho các điểm \(A\left( {1;0;3} \right),B\left( {2;3; - 4} \right),C\left( { - 3;1;2} \right)\). Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.

Cho \ $\int_{0}^{2} f (x) d x = 3$ và $\int_{0}^{2} g (x) d x = 7$ , khi đó $\int_{0}^{2} [f (x) + 3 g (x)] d x$ bằng

Trong không gian với hệ tộa độ Oxyz, cho hai điểm \(A\left( {0;1; - 2} \right)\) và \(B\left( {3; - 1;1} \right)\). Tìm tọa độ của điểm M sao cho $\vec{A M} = 3 \vec{A B}$

Số nghiệm của phương trình \({\log _2}x = 3 - 2{\log _2}\left( {x - 4} \right)\) là

Trong không gian Oxyz, cho hai điểm \(A\left( { - 2;2; - 2} \right)\) và \(B\left( {3; - 3;3} \right)\). Lấy M là điểm thay đổi luôn thỏa mãn \(\frac{{MA}}{{MB}} = \frac{2}{3}\). Giá trị lớn nhất của độ dài đoạn OM bằng

Cho hàm số \(f\left( x \right) = \ln \left( {{x^4} + 1} \right)\). Đạo hàm \(f'\left( 1 \right)\) bằng