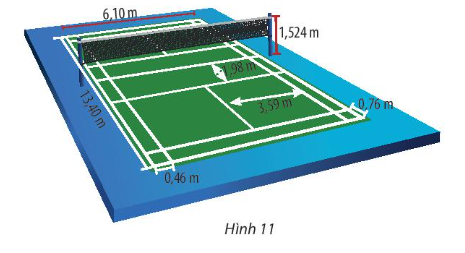
Trong bài toán ứng dụng, khi chơi trên sân cầu lông đơn, các lần phát cầu với thông tin như sau có được cho là hợp lệ không? (Các thông tin không được đề cập thì vẫn giữ như trong giả thiết bài toán trên).
a) Vận tốc xuất phát của cầu là 12m/s.
b) Vị trí phát cầu cách mặt đất là 1,3m.
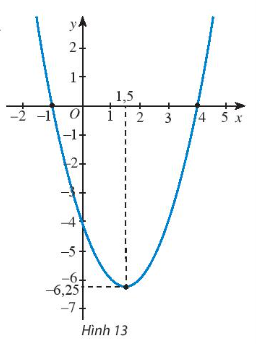
Lưu ý: Các thông số về sân cầu lông được cho trong Hình 11.
Trong bài toán ứng dụng, khi chơi trên sân cầu lông đơn, các lần phát cầu với thông tin như sau có được cho là hợp lệ không? (Các thông tin không được đề cập thì vẫn giữ như trong giả thiết bài toán trên).
a) Vận tốc xuất phát của cầu là 12m/s.
b) Vị trí phát cầu cách mặt đất là 1,3m.
Lưu ý: Các thông số về sân cầu lông được cho trong Hình 11.

Câu hỏi trong đề: Bài tập Hàm số bậc hai có đáp án !!
Quảng cáo
Trả lời:
Ta có hình vẽ sau
a) Theo đề bài, ta có:
g ≈ 9,8 m/s2, α = 30°, v0 = 12m/s, y0 = 0,7 m.
Khi đó, ta có hàm số: y = .
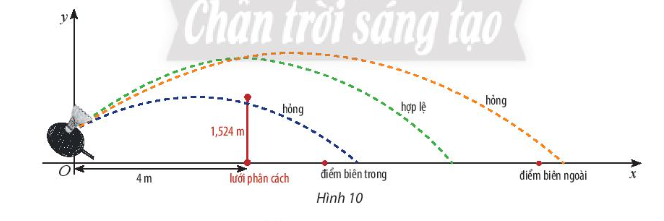
Khi cầu bay tới vị trí lưới phân cách, nếu nó ở bên trên mặt lưới và điểm rơi không ra khỏi đường biên phía bên sân đối phương thì lần phát cầu mới được xem là hợp lệ.
Ta cần so sánh tung độ của điểm quỹ đạo (có hoành độ bằng khoảng cách từ gốc tọa độ đến chân lưới phân cách) với chiều cao mép lưới.
Khi x = 4 (do người đứng cách lưới 4m) ta có:
y =.
Như vậy lần phát cầu này thỏa mãn qua lưới.
Vị trí cầu rơi chạm đất là giao điểm của Parabol với trục hoành nên giải phương trình:
ta được x1 ≈ 13,84 và x2 ≈ -1,11.
Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 13,84m.
Ta có:
Điểm bên trong sẽ cách vị trí phát: 4 + 1,98 = 5, 98m.
Điểm bên ngoài sẽ cách vị trí phát: 4 + 6,7 = 10,7 m.
Do vị trí điểm rơi nằm ngoài khoảng giữa điểm trong và điểm ngoài nên lần phát cầu này hỏng.
Vậy với vận tốc xuất phát của cầu là 12m/s thì lần phát này hỏng (không hợp lệ).
b) Theo đề bài, ta có:
g ≈ 9,8 m/s2, α = 30°, v0 = 8m/s, y0 = 1,3 m.
Khi đó, ta có hàm số: y = .
Khi cầu bay tới vị trí lưới phân cách, nếu nó ở bên trên mặt lưới và điểm rơi không ra khỏi đường biên phía bên sân đối phương thì lần phát cầu mới được xem là hợp lệ.
Ta cần so sánh tung độ của điểm quỹ đạo (có hoành độ bằng khoảng cách từ gốc tọa độ đến chân lưới phân cách) với chiều cao mép lưới.
Khi x = 4 (do người đứng cách lưới 4m) ta có:
y =.
Như vậy lần phát cầu này thỏa mãn qua lưới.
Vị trí cầu rơi chạm đất là giao điểm của Parabol với trục hoành nên giải phương trình:
ta được x1 ≈ 7,38 và x2 ≈ -1,73.
Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 7,38m.
Ta có:
Điểm bên trong sẽ cách vị trí phát: 4 + 1,98 = 5, 98m.
Điểm bên ngoài sẽ cách vị trí phát: 4 + 6,7 = 10,7 m.
Do vị trí điểm rơi nằm trong khoảng giữa điểm trong và điểm ngoài nên lần phát cầu này hợp lệ.
Vậy với vị trí phát cầu cách mặt đất 1,3m thì lần phát cầu này hợp lệ.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét hàm số y = 2x2 + x + m có a = 2, b = 1 và c = m.
Điểm đỉnh S có tọa độ xS = , yS = .
Hàm số có a = 2 > 0 nên giá trị nhỏ nhất của hàm số là m – .
Mà giá trị nhỏ nhất bằng 5 nên m – = 5 ⇔ m = .
Vậy với m = thì giá trị nhỏ nhất của hàm số là 5.
Lời giải
Ta có:
f(0) = a.02 + b.0 + c = 1 ⇔ c = 1.
f(1) = a.12 + b.1 + c = 2 ⇔ a + b + c = 2.
f(2) = a.22 + b.2 + c = 5 ⇔ 4a + 2b + c = 5.
Khi đó, ta có hệ phương trình:
Vậy a = 1, b = 0 và c = 1.
b) Với a = 1, b = 0 và c = 1 thì ta có hàm số: y = x2 + 1.
Xét hàm số bậc hai: y = x2 + 1, có:
Đỉnh S có tọa độ xs = , ys = 02 + 1 = 1. Hay S(0; 1).
Vì hàm số bậc hai có a = 1 > 0 nên ta có bảng biến thiên sau:
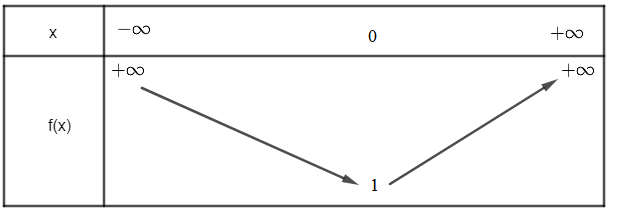
Dựa vào bảng biến thiên ta có:
Hàm số có giá trị nhỏ nhất bằng 1 khi x = 0. Do đó tập giá trị của hàm số là [1; +∞).
Hàm số nghịch biến trên khoảng (-∞;0) và đồng biến trên khoảng (0; +∞).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.