Cho biểu thức $P=\left(\frac{x\sqrt{x}-1}{x-\sqrt{x}}-\frac{x\sqrt{x}+1}{x+\sqrt{x}}\right):\frac{x+2}{x-2}$

1) Tìm điều kiện xác định và rút gọn biểu thức P?

2) Tìm tất cả các giá trị nguyên của x để biểu thức P có giá trị nguyên?

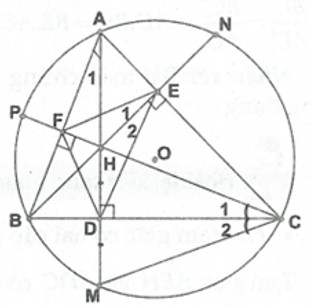
1) AD,BE là đường cao của ∆ABC nên \[\widehat {CEH} = \widehat {HDC} = 90^\circ \]

\[ \Rightarrow \widehat {CEH} + \widehat {HDC} = 180^\circ \]

Suy ra tức giác CEHD là tứ giác nội tiếp (điều cần chứng minh)

Nhận xét: Bài toán chứng minh tứ giác nội tiếp bằng cách chứng minh tổng hai góc đối diện bằng \[180^\circ \]

Tứ giác CEHD có tổng cặp góc đối diện bằng \[180^\circ \]: \[\widehat {CEH} + \widehat {HDC} = 180^\circ \] nên là tứ giác nội tiếp.

2) CF, BE là đường cao của ∆ABC nên \[\widehat {CEB} = \widehat {BFC} = 90^\circ \]

=> Điểm E, F thuộc đường tròn đường kính BC.

=> B, C, E, F cùng nằm trên đường tròn đường kính BC (điều cần chứng minh).

Nhận xét: Bài toán chứng minh bốn điểm cùng nằm trên một đường tròn bằng cách chứng minh hai điểm nhìn một cạnh tạo bởi hai điểm còn lại cùng dưới một góc vuông.

 3) Tam giác AEH và ADH có chung góc tại đỉnh A và \[\widehat {AEH} = \widehat {ADC} = 90^\circ \] nên ∆AEH đồng dạng với ∆ADC \[ \Rightarrow \frac{{AE}}{{AD}} = \frac{{AH}}{{AC}} \Rightarrow AE.AC = AH.AD\] (điều cần chứng minh).

Tam giác BEC và ADC có chung góc tại đỉnh C và \[\widehat {BEC} = \widehat {ADC} = 90^\circ \] nên ∆BEC ∆ADC

\[ \Rightarrow \frac{{BE}}{{AD}} = \frac{{BC}}{{AC}} \Rightarrow AD.BC = CE.AC\] (điều cần chứng minh).

Nhận xét:  Bài toán chứng minh các đẳng thức bằng cách chứng minh các cặp tam giác đồng dạng.

 4) Ta có:

\[\widehat {{A_1}} = \widehat {{C_1}}\] (cùng phụ với \[\widehat {FBC}\]);

\[\widehat {{A_1}} = \widehat {{C_2}}\] (cùng chắn cung của (O));

Suy ra \[\widehat {{C_1}} = \widehat {{C_2}}\]

⇒ CD là phân giác của \[\widehat {HCM}\]

Tam giác CHM có CD vừa là phân giác vừa là đường cao nên cân tại C, suy ra CD đồng thời cũng la trung trực của HM.

⇒ H, M đối xứng với nhau qua BC (điều cần chứng minh).

5) Ta có:

\[\widehat {{E_1}} = \widehat {{C_1}}\] (cùng chắn cung trong đường tròn đi qua bốn điểm B, C, E, F);

\[\widehat {{C_1}} = \widehat {{E_2}}\] (cùng chắn cung trong đường tròn ngoại tiếp tứ giác CEHD);

Suy ra: \[\widehat {{E_1}} = \widehat {{E_2}}\]

⇒ EB là phân giác của \[\widehat {FED}\].

Chứng minh tương tự: FC là phân giác của \[\widehat {DFE}\]

Mà \[FC \cap EB = \left\{ H \right\}\] nên H là tâm đường tròn nội tiếp tam giác DEF.

1) Gọi chữ số hàng chục là x.

Chữ số hàng đơn vị là y.

Vì tổng 2 chữ số là 9, nên ta có \[x + y = 9\]  (1)

Điều kiện: \[0 < x \le 9,\,\,x \in \mathbb{N}*\] và \[0 \le y \le 9,\,\,y \in \mathbb{N}\]

Số đó là \[\overline {xy} = 10x + y\]

Số viết ngược lại là \[\overline {yx} = 10y + x\]

Vì thêm vào số đó 63 đơn vị thì được số mới viết theo thứ tự ngược lại số cũ, ta có

\[\overline {xy} + 63 = \overline {yx} \Rightarrow 10x + y + 63 = 10y + x \Leftrightarrow 9x - 9y = 63\]        (2)

Từ (1) và (2), ta có hệ phương trình

\[\left\{ \begin{array}{l}x + y = 9\\9x - 9y = - 63\end{array} \right.\]

\[ \Leftrightarrow \left\{ \begin{array}{l}x + y = 9\\x - y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x = 2\\x + y = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 8\end{array} \right.\] (thỏa mãn điều kiện)

Vậy số cần tìm là 18.

Nhận xét: Giải bài toán bằng cách lập hệ phương trình từ mỗi quan hệ theo số theo đề bài đã cho từ những kiến thức về cấu tạo số, phép toán số học, …