khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 10
  3. Toán

Câu hỏi:

12/06/2022 11,495 Lưu

Cho đoạn mạch như Hình 1.2. Gọi I là cường độ dòng điện của mạch chính, I1, I2 và I3 là cường độ dòng điện mạch rẽ. Cho biết R1 = 6 Ω, R2 = 8 Ω, I = 3 A và I3 = 2 A. Tính điện trở R3 và hiệu điện thế U giữa hai đầu đoạn mạch.

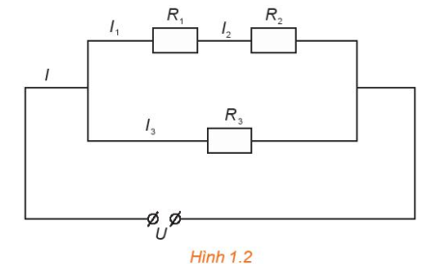
Media VietJack

Xem lời giải

Câu hỏi trong đề: Bài tập Ứng dụng hệ phương trình bậc nhất ba ẩn có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Từ sơ đồ mạch điện, ta có hệ phương trình: I1+I3=IR1I1+R2I2=UR3I3=U

 hay I1+2=36I1+8I2=U2R3=U  (*).

Lại có I1 = I2 nên (*) tương đương với  I1+2=314I1=U2R3=U hay I1=114I1−U=02R3−U=0.

Giải hệ này ta được I1=1A,  R2=7 Ω  và U = 14 V.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cân bằng phương trình phản ứng hoá học đốt cháy octane trong oxygen

C8H18 + O2 → CO2 + H2O.

Lời giải

Giả sử x, y, z, t là bốn số nguyên dương thoả mãn cân bằng phản ứng:

xC8H18 + yO2 → zCO2 + tH2O.

Vì số nguyên tử C, H, O ở hai vế bằng nhau nên ta có hệ: 8x=z18x=2t2y=2z+t⇔8xt=zt9xt=12yt=2zt+1.

Đặt X = xt , Y = yt , Z = zt  ta được hệ phương trình bậc nhất ba ẩn: 8X=Z9X=12Y=2Z+1

 hay 8X−Z=09X−1=02Y−2Z−1=0.

Giải hệ này ta được X =19 , Y =2518 , Z =89.  Từ đây suy ra x = 19 t, y = 2518 t, z = 89. t.

Chọn t = 18 ta được x = 2, y = 25, z = 16. Từ đó ta được phương trình cân bằng:

2C8H18 + 25O2 → 16CO2 + 18H2O.

Câu 2

Một tuyến cáp treo có ba loại vé sau đây: vé đi lên giá 250 nghìn đồng; vé đi xuống giá 200 nghìn đồng và vé hai chiều giá 400 nghìn đồng. Một ngày nhà ga cáp treo thu được tổng số tiền là 251 triệu đồng. Tìm số vé bán ra mỗi loại, biết rằng nhân viên quản lí cáp treo đếm được 680 lượt người đi lên và 520 lượt người đi xuống.

Lời giải

Gọi số vé bán ra loại đi lên, đi xuống và hai chiều lần lượt là x, y, z.

Theo đề bài ta có:

– Nhà ga cáp treo thu được tổng số tiền là 251 triệu đồng, suy ra 250000x + 200000y + 400000z = 251000000 hay 250x + 200y + 400z = 251000 (1).

– Có 680 lượt người đi lên, suy ra x + z = 680 (2).

– Có 520 lượt người đi xuống, suy ra y + z = 520 (3).

Từ (1), (2) và (3) ta có hệ phương trình: 250x+200y+400z=251000x+z=680y+z=520.

Giải hệ này ta được x = 220, y = 40, z = 460.

Vậy số vé bán ra loại đi lên, đi xuống và hai chiều lần lượt là 220, 60, 460.

Câu 3

Em Hà so sánh tuổi của mình với chị Mai và anh Nam. Tuổi của anh Nam gấp ba lần tuổi của em Hà. Cách đây bảy năm tuổi của chị Mai bằng nửa số tuổi của anh Nam. Ba năm nữa tuổi của anh Nam bằng tổng số tuổi của chị Mai và em Hà. Hỏi tuổi của mỗi người là bao nhiêu?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Bác Việt có 330740 nghìn đồng, bác chia số tiền này thành ba phần và đem đầu tư vào ba hình thức : Phần thứ nhất bác đầu tư vào chứng khoán với lãi thu được 4% một năm; phần thứ hai bác mua vàng thu lãi 5% một năm và phần thứ ba bác gửi tiết kiệm với lăii suất 6% một năm. Sau một năm, kể cả gốc và lãi bác thu được ba món tiền bằng nhau. Hỏi tổng số tiền cả gốc và lãi bác thu được sau một năm là bao nhiêu?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hàm cung và hàm cầu của ba mặt hàng như sau :QS1=−4+x; QD1=70−x−2y−6z;QS2=−3+y;QD2=76−3x−y−4z;QS3=−6+3z;QD3=70−2x−3y−2z.

Hãy xác định giá cân bằng cung – cầu của ba mặt hàng.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Ba lớp 10A, 10B, 10C của một trường trung học phồ thông gồm 128 em cùng tham gia lao động trồng cây. Tính trung bình, mỗi em lớp 10A trồng được 3 cây xoan và 4 cây bạch đàn; mỗi em lớp 10B trồng được 2 cây xoan và 5 cây bạch đàn; mối em lớp 10 C trồng được 6 cây xoan. Cả ba lớp trồng được tổng cộng 476 cây xoan và 375 cây bạch đàn. Hỏi mỗi lớp có bao nhiêu em?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập