Câu hỏi:

11/07/2024 2,684

Cho x, y là hai số thực thỏa mãn : \[x > y\] và \[xy = 1\]. Chứng minh rằng \[\frac{{{{\left( {{x^2} + {y^2}} \right)}^2}}}{{{{\left( {x - y} \right)}^2}}} \ge 8\]

Xem lời giải

Câu hỏi trong đề: Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Vì \[x > y\] nên \[x - y > 0,\] suy ra \[\frac{{{{\left( {{x^2} + {y^2}} \right)}^2}}}{{{{\left( {x - y} \right)}^2}}} \ge 8 \Leftrightarrow \frac{{{x^2} + {y^2}}}{{x - y}} \ge 2\sqrt 2 \]

\[ \Leftrightarrow {x^2} + {y^2} \ge 2\sqrt 2 \left( {x - y} \right) \Leftrightarrow {x^2} + {y^2} - 2\sqrt 2 x + 2\sqrt 2 y \ge 0\]

\[ \Leftrightarrow {x^2} + {y^2} + 2 - 2\sqrt 2 x + 2\sqrt 2 y \ge 0 \Leftrightarrow {x^2} + {y^2} + {\left( {\sqrt 2 } \right)^2} - 2\sqrt 2 x + 2\sqrt 2 y - 2xy \ge 0\]

(vì\[xy = 1\] nên \[2 = 2xy\])

\[{\left( {x - y - \sqrt 2 } \right)^2} \ge 0\], điều này luôn luôn đúng

Vậy ta có điều phải chứng minh.

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác \[\Delta ABC\] vuông ở A. Trên cạnh AC lấy 1 điểm M, dựng đường tròn tâm (O) có đường kính MC. Đường thẳng BM cắt đường tròn tâm (O) tại D, đường thẳng AD cắt đường tròn tâm (O) tại S

1) Chứng minh tứ giác ABCD là tứ giác nội tiếp và CA là tia phân giác của góc \[\widehat {BCS}\]

2) Gọi E là giao điểm của BC với đường tròn (O). Chứng minh các đường thẳng BA, EM, CD đồng quy

3) Chứng minh M là tâm đường tròn nội tiếp tam giác \[\Delta ADE\]

Xem đáp án

Lời giải

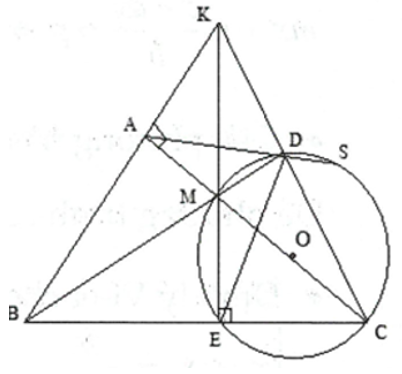
Cho tam giác ABC vuông ở A. Trên cạnh AC lấy 1 điểm M, dựng đường tròn tâm (O) có đường kính MC. Đường thẳng BM cắt đường (ảnh 1)

1) Ta có \[\widehat {BAC} = 90^\circ \left( {gt} \right)\]

\[\widehat {MDC} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn )

A, D nhìn BC dưới góc \[90^\circ \] , tứ giác ABCD nội tiếp

Vì tứ giác ABCD nội tiếp \[ \Rightarrow \widehat {ADB} = \widehat {ACB}\](cùng chắn cung AB) (1)

Ta có tứ giác DMCS nội tiếp \[ \Rightarrow \widehat {ADB} = \widehat {ACS}\](cùng bù với\[\widehat {MDS}\]) (2)

Từ (1) và (2) \[ \Rightarrow \widehat {BCA} = \widehat {ACS}\]

2) Giả sử BA cắt CD tại K. Ta có \[BD \bot CK,CA \bot BK\]

\[ \Rightarrow M\] là trực tâm \[\Delta KBC\]. Mặt khác \[\widehat {MEC} = 90^\circ \](góc nội tiếp chắn nửa đường tròn)

\[ \Rightarrow K,M,E\] thẳng hàng, hay BA, EM, CD đồng quy tại K

3) Vì tứ giác ABCD nội tiếp \[ \Rightarrow \widehat {DAC} = \widehat {DBC}\](cùng chắn ) (3)

Mặt khác tứ giác BAME nội tiếp \[ \Rightarrow \widehat {MAE} = \widehat {MBE}\](cùng chắn ) (4)

Từ (3) và (4) \[ \Rightarrow \widehat {DAM} = \widehat {MAE}\] hay AM là tia phân giác \[\widehat {DAE}\]

Chứng minh tương tự \[\widehat {ADM} = \widehat {MDE}\] hay DM là tia phân giác \[\widehat {ADE}\]

Vậy M là tâm đường tròn nội tiếp \[\Delta ADE\]

Câu 2

Cho biểu thức \[P = \left( {\frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{1}{{x - \sqrt x }}} \right):\left( {\frac{1}{{\sqrt x + 1}} + \frac{2}{{x - 1}}} \right)\]

1) Tìm điều kiện xác định và rút gọn biểu thức P?

2) Tìm m thỏa mãn \[P\sqrt x = m - \sqrt x ?\]

Xem đáp án

Lời giải

1) Điều kiện xác định : \[\left\{ \begin{array}{l}x \ge 0\\\sqrt x - 1 \ne 0\\x - \sqrt x \ne 0\\\sqrt x + 1 \ne 0\\x - 1 \ne 0\\\frac{1}{{\sqrt x + 1}} + \frac{2}{{x - 1}} \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 0\\x \ne 1\end{array} \right. \Leftrightarrow 0 < x \ne 1\]

Ta có : \[P = \left[ {\frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{1}{{\sqrt x \left( {\sqrt x - 1} \right)}}} \right]:\left[ {\frac{{\sqrt x - 1}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} + \frac{2}{{x - 1}}} \right]\]

\[ = \left[ {\frac{{x - 1}}{{\left( {\sqrt x - 1} \right)\sqrt x }}} \right]\] \[:\left( {\frac{{\sqrt x - 1 + 2}}{{x - 1}}} \right)\]

\[ = \left[ {\frac{{x - 1}}{{\left( {\sqrt x - 1} \right)\sqrt x }}} \right].\left( {\frac{{x - 1}}{{\sqrt x + 1}}} \right)\] \[ = \frac{{{{\left( {x - 1} \right)}^2}}}{{\left( {x - 1} \right)\sqrt x }}\] \[ = \] \[\frac{{x - 1}}{{\sqrt x }}\]

Vậy \[P = \frac{{x - 1}}{{\sqrt x }}\]

Cách 2: Đặt \[a = \sqrt x \left( {a \ge 0} \right)\]

Ta có

\[P = \left( {\frac{a}{{a - 1}} - \frac{1}{{{a^2} - a}}} \right):\left( {\frac{1}{{a + 1}} + \frac{2}{{{a^2} - 1}}} \right) = \left[ {\frac{a}{{a - 1}} - \frac{1}{{a\left( {a - 1} \right)}}} \right]:\left[ {\frac{1}{{a + 1}} + \frac{2}{{\left( {a - 1} \right)\left( {a + 1} \right)}}} \right]\]

\[ = \frac{{{a^2} - 1}}{{a\left( {a - 1} \right)}}:\frac{{\left( {a - 1} \right) + 2}}{{a + 1}} = \frac{{\left( {a - 1} \right)\left( {a + 1} \right)}}{{a\left( {a - 1} \right)}}:\frac{{a + 1}}{{a + 1}} = \frac{{a + 1}}{a} = \frac{{\sqrt x + 1}}{{\sqrt x }}\]

Nhận xét : Bài toán rút gọn biểu thức có chứa biến

2) Ta có : \[P\sqrt x = m - \sqrt x \Leftrightarrow \frac{{x - 1}}{{\sqrt x }}.\sqrt x = m - \sqrt x \]

\[ \Leftrightarrow x - 1 = m - \sqrt x \Leftrightarrow m = x - 1 + \sqrt x \]

Vậy \[m = x - 1 + \sqrt x \]với \[0 < x \ne 1\]

Nhận xét : Bài toán tìm tham số để thỏa mãn một đẳng thức cho trước

Câu 3