Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất) - Đề số 9

1) Điều kiện xác định : \[\left\{ \begin{array}{l}x \ge 0\\\sqrt x  - 1 \ne 0\\x - \sqrt x  \ne 0\\\sqrt x  + 1 \ne 0\\x - 1 \ne 0\\\frac{1}{{\sqrt x  + 1}} + \frac{2}{{x - 1}} \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 0\\x \ne 1\end{array} \right. \Leftrightarrow 0 < x \ne 1\]

Ta có : \[P = \left[ {\frac{{\sqrt x }}{{\sqrt x  - 1}} - \frac{1}{{\sqrt x \left( {\sqrt x  - 1} \right)}}} \right]:\left[ {\frac{{\sqrt x  - 1}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}} + \frac{2}{{x - 1}}} \right]\]

\[ = \left[ {\frac{{x - 1}}{{\left( {\sqrt x  - 1} \right)\sqrt x }}} \right]\] \[:\left( {\frac{{\sqrt x  - 1 + 2}}{{x - 1}}} \right)\]

\[ = \left[ {\frac{{x - 1}}{{\left( {\sqrt x  - 1} \right)\sqrt x }}} \right].\left( {\frac{{x - 1}}{{\sqrt x  + 1}}} \right)\] \[ = \frac{{{{\left( {x - 1} \right)}^2}}}{{\left( {x - 1} \right)\sqrt x }}\] \[ = \] \[\frac{{x - 1}}{{\sqrt x }}\]

Vậy \[P = \frac{{x - 1}}{{\sqrt x }}\]

Cách 2: Đặt \[a = \sqrt x \left( {a \ge 0} \right)\]

Ta có

\[P = \left( {\frac{a}{{a - 1}} - \frac{1}{{{a^2} - a}}} \right):\left( {\frac{1}{{a + 1}} + \frac{2}{{{a^2} - 1}}} \right) = \left[ {\frac{a}{{a - 1}} - \frac{1}{{a\left( {a - 1} \right)}}} \right]:\left[ {\frac{1}{{a + 1}} + \frac{2}{{\left( {a - 1} \right)\left( {a + 1} \right)}}} \right]\]

\[ = \frac{{{a^2} - 1}}{{a\left( {a - 1} \right)}}:\frac{{\left( {a - 1} \right) + 2}}{{a + 1}} = \frac{{\left( {a - 1} \right)\left( {a + 1} \right)}}{{a\left( {a - 1} \right)}}:\frac{{a + 1}}{{a + 1}} = \frac{{a + 1}}{a} = \frac{{\sqrt x  + 1}}{{\sqrt x }}\]

Nhận xét : Bài toán rút gọn biểu thức có chứa biến

2) Ta có : \[P\sqrt x  = m - \sqrt x  \Leftrightarrow \frac{{x - 1}}{{\sqrt x }}.\sqrt x  = m - \sqrt x \]

\[ \Leftrightarrow x - 1 = m - \sqrt x  \Leftrightarrow m = x - 1 + \sqrt x \]

Vậy \[m = x - 1 + \sqrt x \]với \[0 < x \ne 1\]

Nhận xét : Bài toán tìm tham số để thỏa mãn một đẳng thức cho trước

1) Gọi x và y lần lượt là số cầu thủ của mỗi đội (x, y nguyên dương)

Giả sử x là số lẻ

Vì mỗi cầu thủ của đội này phải thi đấu với mỗi cầu thủ của đội kia một trận nên tổng số trận đấu là x.y

Vì tổng số trận đấu bằng 4 lần tổng số cầu thủ của cả 2 đội nên ta có phương trình \[x.y = 4\left( {x + y} \right)\]

\[ \Leftrightarrow x.y - 4x - 4y + 16 = 16 \Leftrightarrow \left( {x - 4} \right)\left( {y - 4} \right) = 16\]

Vì x, y là số nguyên dương nên : \[x - 4 \ge  - 3\] và \[y - 4 \ge  - 3\]

Mặt khác x là số lẻ nên \[x - 4\] là số lẻ

Mà 16 chỉ phân tích được thành tích của 2 số trong đó có một số lẻ là : \[16 = 1.16\]

\[ \Leftrightarrow \left\{ \begin{array}{l}x - 4 = 1\\y - 4 = 16\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 20\end{array} \right.\](thỏa mãn điều kiện )

Vậy một đội có 5 cầu thủ, đội còn lại có 20 cầu thủ

2)

a) Với \[m = 1\], ta có \[\left( d \right):2x + 8\]

Phương trình hoành độ giao điểm của đường thẳng (d) với đồ thị (P) là :

\[{x^2} = 2x + 8 \Leftrightarrow {x^2} - 2x - 8 = 0 \Leftrightarrow {x^2} + 2x - 4x - 8 = 0\]

\[ \Leftrightarrow x\left( {x + 2} \right) - 4\left( {x + 2} \right) = 0 \Leftrightarrow \left( {x + 2} \right)\left( {x - 4} \right) = 0\]

\[ \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - 2 \Rightarrow y = 2.\left( { - 2} \right) + 8 = 4\\x = 4 \Rightarrow y = 2.4 + 8 = 16\end{array} \right.\]

Vậy tọa độ các giao điểm của (d) và (P) là \[\left( { - 2;4} \right)\] và \[\left( {4;16} \right)\]

b) Phương trình hoành độ của đường thẳng (d) và đồ thị (P) là :

\[{x^2} = 2x - {m^2} + 9 \Leftrightarrow {x^2} - 2x + \left( {{m^2} - 9} \right) = 0\left( 1 \right)\]

Để đường thẳng (d) cắt Parabol (P) tại hai điểm nằm về hai phía của trục tung thì phương trình (1) có hai nghiệm trái dấu \[ \Leftrightarrow 1\left( {{m^2} - 9} \right) < 0\]

\[ \Leftrightarrow {m^2} - 9 < 0 \Leftrightarrow \left( {m - 3} \right)\left( {m + 3} \right) < 0 \Leftrightarrow  - 3 < m < 3\]

Vậy \[ - 3 < m < 3\] thì đường thẳng (d) cắt parabol (P) tại hai điểm nằm về hai phía của trục tung

1) Hệ phương trình tương đương với : \[\left\{ \begin{array}{l}{x^2} - \frac{{x\left( {2x - 1} \right)}}{3} = 24\\\frac{{2x - 1}}{3} = y\end{array} \right.\]

\[ \Leftrightarrow \left\{ \begin{array}{l}{x^2} + x = 72\\\frac{{2x - 1}}{3} = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} + 9x = 8x + 72\\\frac{{2x - 1}}{3} = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x\left( {x + 9} \right) = 8\left( {x + 9} \right)\\\frac{{2x - 1}}{3} = y\end{array} \right.\]

\[ \Leftrightarrow \left\{ \begin{array}{l}\left( {x + 9} \right)\left( {x - 8} \right) = 0\\\frac{{2x - 1}}{3} = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x =  - 9\\x = 8\end{array} \right.\\\frac{{2x - 1}}{3} = y\end{array} \right.\left\{ \begin{array}{l}\left[ \begin{array}{l}x =  - 9\\x = 8\end{array} \right.\\\frac{{2x - 1}}{3} = y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 9\\y =  - \frac{{19}}{3}\end{array} \right. \vee \left\{ \begin{array}{l}x = 8\\y = 5\end{array} \right.\]

Vậy hệ phương trình có nghiệm : \[\left( {x;y} \right) = \left( { - 9; - \frac{{19}}{3}} \right),\left( {8;5} \right)\]

2) Phương trình tương đương với : \[\frac{{\left( {x + 5} \right).6}}{{2.6}} + \frac{{\left( {3 - 2x} \right).3}}{{4.3}} = \frac{{12x}}{{12}} - \frac{{\left( {7 + x} \right).2}}{{6.2}}\]

\[ \Leftrightarrow \left( {x + 5} \right).6 + \left( {3 - 2x} \right).3 = 12x - \left( {7 + x} \right).2 \Leftrightarrow 39 = 10x - 14 \Leftrightarrow x = \frac{{53}}{{10}}\]

 3) Để phương trình có 2 nghiệm phân biệt \[{x_1},{x_2}\] thì \[\Delta  > 0\]

\[ \Leftrightarrow {\left( {2m - 1} \right)^2} - 4.2\left( {m - 1} \right) > 0 \Leftrightarrow {\left( {3 - 2m} \right)^2} > 0 \Leftrightarrow 3 - 2m \ne 0 \Leftrightarrow m \ne \frac{3}{2}\]

Theo định lý Vi-ét, ta có \[\left\{ \begin{array}{l}{x_1} + {x_2} =  - \frac{{2m - 1}}{2} = \frac{{1 - 2m}}{2}\\{x_1}.{x_2} = \frac{{m - 1}}{2}\end{array} \right.\]

Kết hợp với yêu cầu đề bài, ta có hệ phương trình \[\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{1 - 2m}}{2}\\{x_1}{x_2} = \frac{{m - 1}}{2}\\3{x_1} - 4{x_2} = 11\end{array} \right.\]

\[ \Leftrightarrow \left\{ \begin{array}{l}4{x_2} = 3{x_1} - 11\\4{x_1} + 4{x_2} = 2\left( {1 - 2m} \right)\\4{x_1}.{x_2} = 2\left( {m - 1} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4{x_2} = 3{x_1} - 11\\4{x_1} + \left( {3{x_1} - 11} \right) = 2\left( {1 - 2m} \right)\\{x_1}\left( {3{x_1} - 11} \right) = 2\left( {m - 1} \right)\end{array} \right.\] \[ \Leftrightarrow \left\{ \begin{array}{l}4{x_2} = 3{x_1} - 11\\2m = \frac{{13 - 7{x_1}}}{2}\\3{x_1}^2 - 11{x_1} = 2m - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4{x_2} = 3{x_1} - 11\\2m = \frac{{13 - 7{x_1}}}{2}\\3{x_1}^2 - 11{x_1} = \frac{{13 - 7{x_1}}}{2} - 2\end{array} \right.\]

\[ \Leftrightarrow \left\{ \begin{array}{l}{x_1} = 3\\{x_2} =  - \frac{1}{2}\\m =  - 2\end{array} \right.\] hoặc \[\left\{ \begin{array}{l}{x_1} =  - \frac{1}{2}\\{x_2} =  - \frac{{25}}{8}\\m = \frac{{33}}{8}\end{array} \right.\]

Cả hai giá trị m tìm được đều thỏa mãn điều kiện để phương trình có 2 nghiệm

Vậy \[m =  - 2\] hoặc \[m = \frac{{33}}{8}\]

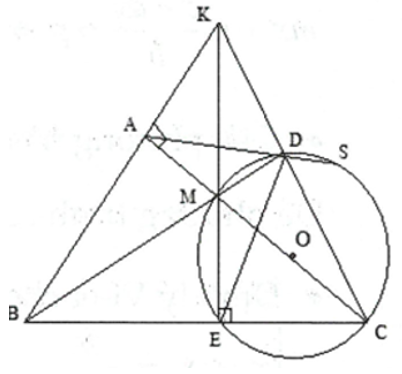
1) Ta có \[\widehat {BAC} = 90^\circ \left( {gt} \right)\]

\[\widehat {MDC} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn )

A, D nhìn BC dưới góc \[90^\circ \] , tứ giác ABCD nội tiếp

Vì tứ giác ABCD nội tiếp \[ \Rightarrow \widehat {ADB} = \widehat {ACB}\](cùng chắn cung AB) (1)

Ta có tứ giác DMCS nội tiếp \[ \Rightarrow \widehat {ADB} = \widehat {ACS}\](cùng bù với\[\widehat {MDS}\])    (2)

Từ (1) và (2) \[ \Rightarrow \widehat {BCA} = \widehat {ACS}\]

2) Giả sử BA cắt CD tại K. Ta có \[BD \bot CK,CA \bot BK\]

\[ \Rightarrow M\] là trực tâm \[\Delta KBC\]. Mặt khác \[\widehat {MEC} = 90^\circ \](góc nội tiếp chắn nửa đường tròn)

\[ \Rightarrow K,M,E\] thẳng hàng, hay BA, EM, CD đồng quy tại K

3) Vì tứ giác ABCD nội tiếp \[ \Rightarrow \widehat {DAC} = \widehat {DBC}\](cùng chắn )       (3)

Mặt khác tứ giác BAME nội tiếp \[ \Rightarrow \widehat {MAE} = \widehat {MBE}\](cùng chắn ) (4)

Từ (3) và (4) \[ \Rightarrow \widehat {DAM} = \widehat {MAE}\] hay AM là tia phân giác \[\widehat {DAE}\]

Chứng minh tương tự \[\widehat {ADM} = \widehat {MDE}\] hay DM là tia phân giác \[\widehat {ADE}\]

Vậy M là tâm đường tròn nội tiếp \[\Delta ADE\]

Vì \[x > y\] nên \[x - y > 0,\] suy ra \[\frac{{{{\left( {{x^2} + {y^2}} \right)}^2}}}{{{{\left( {x - y} \right)}^2}}} \ge 8 \Leftrightarrow \frac{{{x^2} + {y^2}}}{{x - y}} \ge 2\sqrt 2 \]

\[ \Leftrightarrow {x^2} + {y^2} \ge 2\sqrt 2 \left( {x - y} \right) \Leftrightarrow {x^2} + {y^2} - 2\sqrt 2 x + 2\sqrt 2 y \ge 0\]

\[ \Leftrightarrow {x^2} + {y^2} + 2 - 2\sqrt 2 x + 2\sqrt 2 y \ge 0 \Leftrightarrow {x^2} + {y^2} + {\left( {\sqrt 2 } \right)^2} - 2\sqrt 2 x + 2\sqrt 2 y - 2xy \ge 0\]

(vì\[xy = 1\] nên \[2 = 2xy\])

\[{\left( {x - y - \sqrt 2 } \right)^2} \ge 0\], điều này luôn luôn đúng

Vậy ta có điều phải chứng minh.