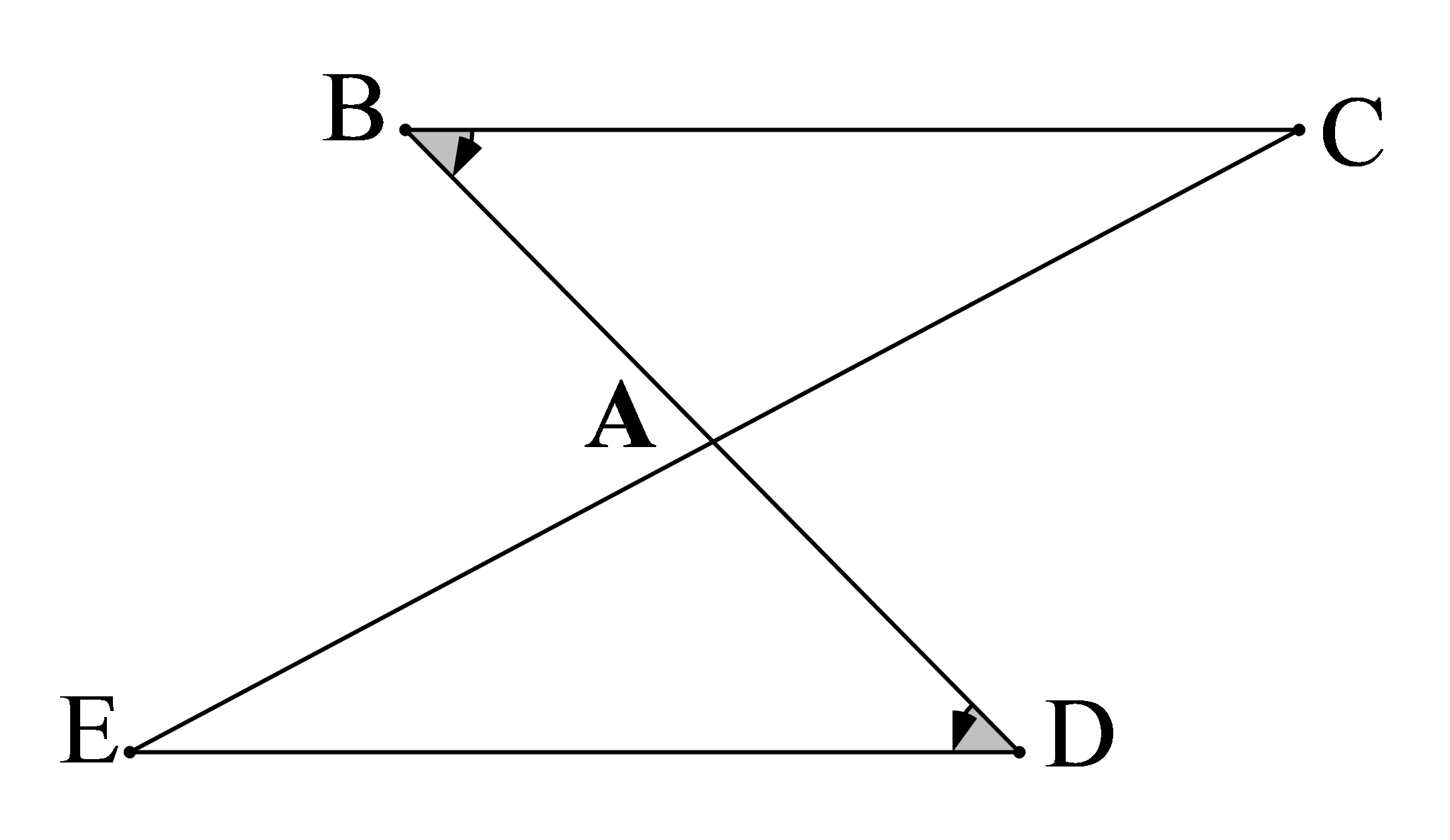✕

✨ Đăng kí VIP để truy cập không giới hạn. Đăng ký ngay

Câu hỏi:

22/06/2022 925

Cho hình vẽ sau:

Tọa độ điểm M là:

A. (2; −1)

B. (−2; 1)

C. (1; −2)

D. (−1; 2)

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra học kì 1 Toán 7 có đáp án ( Mới nhất) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

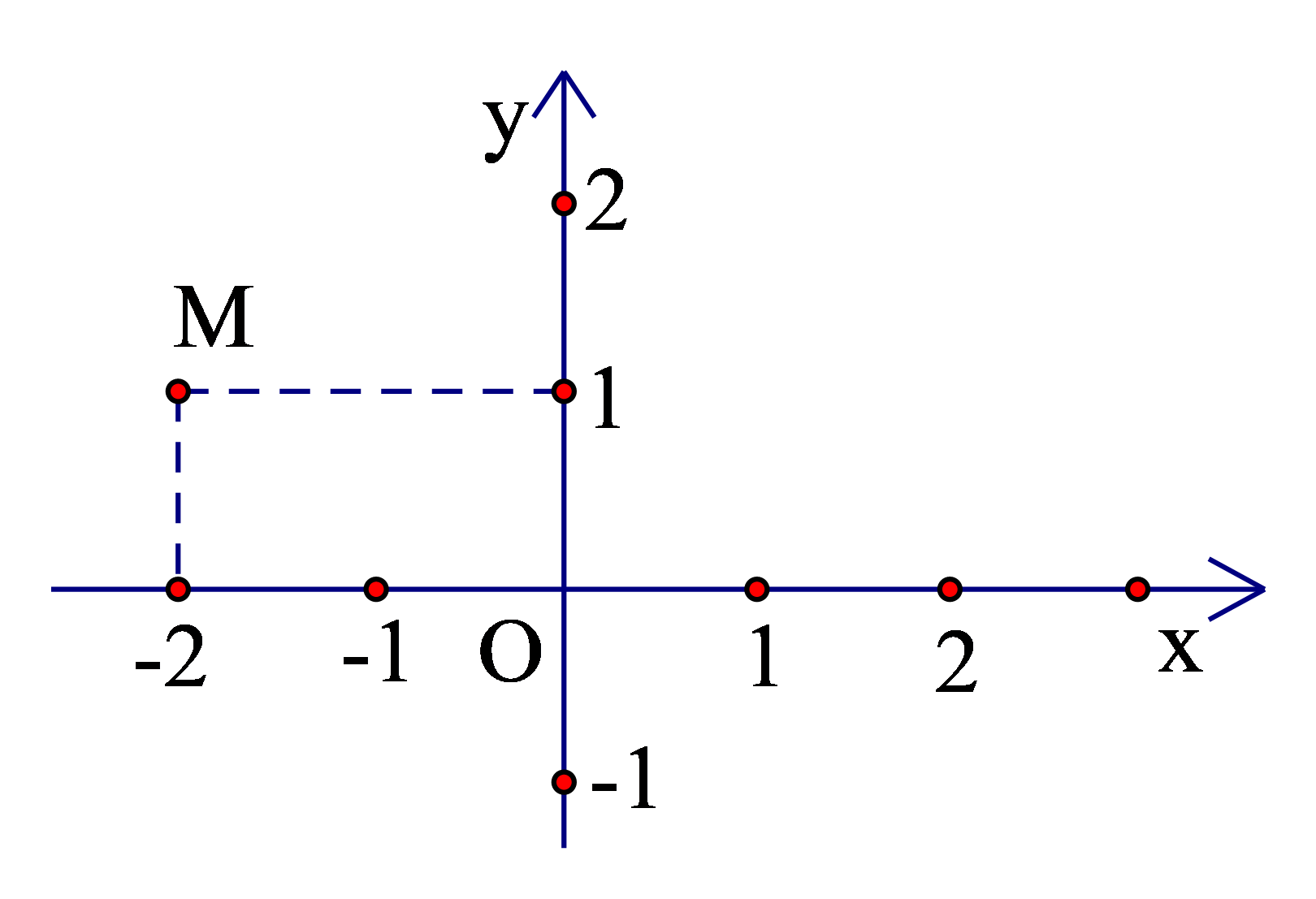
Cho hình vẽ sau: Tọa độ điểm M là: (ảnh 2)

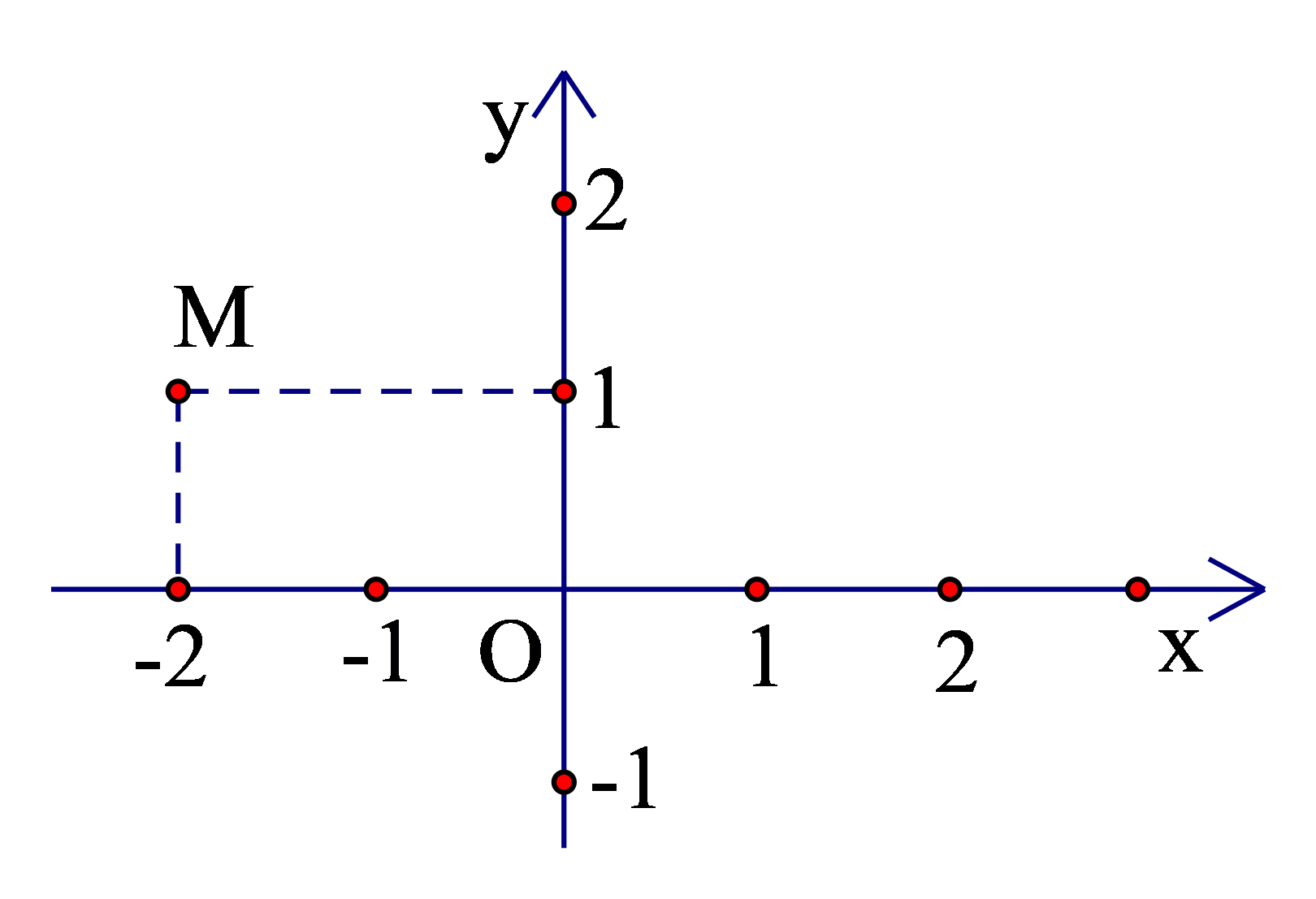
Dựa vào đồ thị hàm số, ta thấy điểm M có hoành độ bằng −2 và tung độ bằng 1.

Do đó, điểm M (−2; 1).

Đáp án B

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm x, y biết: $\frac{1 + 3 y}{12} = \frac{1 + 5 y}{5 x} = \frac{1 + 7 y}{4 x}$ .

Xem đáp án

Lời giải

ĐK: x $\neq$ 0.

Ta có: $\frac{1 + 3 y}{12} = \frac{1 + 5 y}{5 x} = \frac{1 + 7 y}{4 x}$ (*)

Suy ra: $\frac{1 + 3 y}{12} = \frac{1 + 5 y}{5 x}$ và $\frac{1 + 5 y}{5 x} = \frac{1 + 7 y}{4 x}$ .

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

$\frac{1 + 3 y}{12} = \frac{1 + 5 y}{5 x}$ $= \frac{1 + 3 y - (1 + 5 y)}{12 - 5 x} = \frac{1 + 3 y - 1 - 5 y}{12 - 5 x} = \frac{- 2 y}{12 - 5 x}$ (1)

$\frac{1 + 5 y}{5 x} = \frac{1 + 7 y}{4 x} = \frac{1 + 5 y - (1 + 7 y)}{5 x - 4 x} = \frac{1 + 5 y - 1 - 7 y}{5 x - 4 x} = \frac{- 2 y}{x}$

(2)

Từ (1) và (2) suy ra: $\frac{- 2 y}{12 - 5 x}$ = $\frac{- 2 y}{x}$ (3)

- Nếu y = 0 thay vào (*), ta được: $\frac{1}{12} = \frac{1}{5 x} = \frac{1}{4 x}$

Mà x 0 nên không có giá trị x thỏa mãn (*).

- Nếu y 0:

Từ (3) suy ra: x = 12 – 5x

x + 5x = 12

6x = 12

x = 2 (thỏa mãn)

Thay x = 2 vào (*) ta được:

$\frac{1 + 3 y}{12} = \frac{1 + 5 y}{10} = \frac{1 + 7 y}{8}$

$\Rightarrow \frac{1}{12} + \frac{1}{4} y = \frac{1}{10} + \frac{1}{2} y$

$\Rightarrow \frac{1}{4} y = \frac{- 1}{60}$

$\Rightarrow y = \frac{- 1}{15}$ (thỏa mãn)

Vậy x = 2, $y = \frac{- 1}{15}$ thoả mãn yêu cầu bài toán.

Câu 2

Cho góc nhọn xOy. Trên tia Ox lấy điểm A, B sao cho OA = 3 cm, OB = 5cm. Trên tia Oy lấy điểm C, D sao cho OC = OA, OD = OB. Nối AD và BC cắt nhau tại I.

a) Chứng minh: ∆OAD = ∆OCB.

b) Chứng minh: IA = IC.

c) Chứng minh: OI là tia phân giác của $\hat{x O y}$ .

Xem đáp án

Lời giải

Cho góc nhọn xOy. Trên tia Ox lấy điểm A, B sao cho OA = 3 cm, OB = 5cm. Trên tia Oy lấy điểm C, D sao cho OC = OA, OD = OB. Nối AD và BC cắt nhau tại I. a) Chứng minh: ∆OAD = ∆OCB. b) Chứng minh: IA = IC. c) Chứng minh: OI là tia phân giác của góc x0y. (ảnh 1)

a) Chứng minh: ∆OAD = ∆OCB.

Ta có: OA + AB = OB

OC + CD = OD

Mà OA = OC = 3cm, OD = OB = 5cm.

Nên AB = CD.

Xét ∆OAD và ∆OCB có:

OD = OB (gt)

$\hat{A O D}$ chung

OA = OC (gt).

Do đó ∆OAD = ∆OCB (c.g.c).

b) Chứng minh: IA = IC.

∆OAD = ∆OCB (câu a)

Suy ra: $\hat{O C B} = \hat{O A D}$ , $\hat{O B C} = \hat{O D A}$ (các cặp góc tương ứng).

Ta có: $\hat{O C B} + \hat{B C D} = 180^{o}$

$\hat{O A D} + \hat{B A D} = 180^{o}$

Mà $\hat{O C B} = \hat{O A D}$

Do đó: $\hat{B C D} = \hat{B A D}$ .

Xét ∆ICD và ∆IAB có:

$\hat{O B C} = \hat{O D A}$ (cmt)

CD = AB (cmt)

$\hat{B C D} = \hat{B A D}$ (cmt)

Do đó ∆ICD = ∆IAB (g.c.g).

Suy ra IA = IC (hai cạnh tương ứng).

c) Chứng minh: OI là tia phân giác của $\hat{x O y}$ .

Xét ∆OIC và ∆OAI có:

OC = OA (gt)

IC = IA (cmt)

Cạnh OI chung

Do đó ∆OIC = ∆OAI (c.c.c).

Suy ra: $\hat{I O D} = \hat{I O B}$ (hai góc tương ứng).

Vậy OI là tia phân giác của $\hat{x O y}$ .

Câu 3

Tìm x, biết:

a) $(0,5 x - \frac{3}{7}) : \frac{1}{2} = 1 \frac{1}{7}$

b) |2 − 3x| − 5 = −1

c) ${(\frac{1}{5} - \frac{3}{2} x)}^{2} = \frac{9}{4}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Một tam giác có chu vi bằng 36cm, ba cạnh của tam giác đó lần lượt tỉ lệ thuận với 3; 4; 5. Tính độ dài ba cạnh của tam giác đó.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Nếu góc xOy có số đo bằng 47^o thì số đo của góc đối đỉnh với góc xOy bằng bao nhiêu?

A. 133^o

B. 43^o

C. 74^o

D. 47^o

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho góc nhọn xOy. Trên tia Ox lấy điểm A, B sao cho OA = 3 cm, OB = 5cm. Trên tia Oy lấy điểm C, D sao cho OC = OA, OD = OB. Nối AD và BC cắt nhau tại I.

a) Chứng minh: ∆OAD = ∆OCB.

b) Chứng minh: IA = IC.

c) Chứng minh: OI là tia phân giác của $\hat{x O y}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Vietjack official store

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

🔥 Đề thi HOT:

Bạn vui lòng để lại thông tin để được
TƯ VẤN THÊM

Hoặc gọi Hotline tư vấn: 084 283 45 85
Email: vietjackteam@gmail.com

VietJack