Câu hỏi:
27/06/2022 115Cho khối lăng trụ \(ABC.A'B'C'\) có thể tích bằng 1. Gọi M, N lần lượt là trung điểm các đoạn thẳng \(AA',BB'.\) Mặt phẳng \(\left( {CMN} \right)\) cắt các đường thẳng \(C'A',C'B'\) lần lượt tại P, Q. Thể tích của khối đa diện lồi \(AA'P.BB'Q\) bằng
Đáp án chính xác
Câu hỏi trong đề:
Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án B
Dễ thấy \(AP,BQ,CC'\) đồng quy nên đa diện lồi \(ABCPQC'\) là khối chóp cụt.
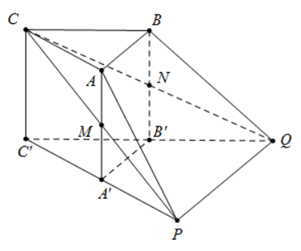
Đặt \[{{\rm{S}}_{ABC}} = S\], chiều cao lăng trụ là h thì \[{S_{C'PQ}} = 4S\] ta có \(Sh = 1\) và thể tích chóp cụt \(ABCPQC'\) là:
\({V_{ABCPQC'}} = \frac{1}{3}\left( {S + \sqrt {S.4S} + 4S} \right).h\)
\( = \frac{1}{3}.7.S.h = \frac{7}{3} \Rightarrow {V_{AA'PBB'Q}} = \frac{7}{3} - 1 = \frac{4}{3}.\)Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho phương trình \(\log _3^2\left( {3x} \right) - \left( {m + 2} \right){\log _3}x + m - 2 = 0\) (m là tham số thực). Tập hợp tất cả các giá trị của m để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn \(\left[ {\frac{1}{3};3} \right]\) là
Xem đáp án »
27/06/2022
4,835
Câu 2:
Biết \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {a;b} \right]\) và \(2F\left( a \right) - 7 = 2F\left( b \right)\). Tính tích phân \(I = \int\limits_a^b {f\left( x \right)} dx.\)
Xem đáp án »
27/06/2022
3,166
Câu 3:
Cho hàm số \(f\left( x \right)\) có đồ thị hàm số \(y = f'\left( x \right)\) được cho như hình vẽ bên. Hàm số \(y = \left| {f\left( x \right) + \frac{1}{2}{x^2} - f\left( 0 \right)} \right|\) có nhiều nhất bao nhiêu điểm cực trị trong khoảng \(\left( { - 2;3} \right)\)?
Xem đáp án »
27/06/2022
3,047
Câu 4:
Cho các số thực dương a, b thỏa mãn \({\log _4}a = {\log _6}b = {\log _9}\left( {4a - 5b} \right) - 1.\) Đặt \(T = \frac{b}{a}.\) Khẳng định nào sau đây đúng?
Xem đáp án »
27/06/2022
1,821
Câu 5:
Có 3 kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và 4 kiểu dây (kim loại, da, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?
Xem đáp án »
27/06/2022
1,214
Câu 6:
Một mảnh giấy hình quạt như hình vẽ có bán kính \(AB = AC = 8\,\,cm.\) Người ta dán mép AB và AC lại với nhau để được một hình nón đỉnh A. Biết độ dài cung BC bằng \(8\pi \sqrt 3 \,\,cm,\) tính thể tích V của khối nón thu được (xem phần giấy dán không đáng kể)
Xem đáp án »
27/06/2022
1,163
Câu 7:
Tất cả các nguyên hàm của hàm số \(f\left( x \right) = {3^{ - x}}\) là
Xem đáp án »
27/06/2022
1,155
về câu hỏi!