Cho hình lăng trụ (ABC.A'B'C' )có đáy (ABC ) là tam giác vuông tại (B ) và (A'A = A'B = A'C ). Biết rằng (AB = 2a ), (BC = sqrt 3 a ) và mặt phẳng ( left( {A'BC} right) ) tạo với mặt phẳng đáy một gó...

Đáp án C Phương pháp giải: - Vì [A'A = A'B = A'C ] nên hình chiếu vuông góc của [A' ] lên [ left( {ABC} right) ] trùng với tâm đường tròn ngoại tiếp [ Delta ABC ]. - Xác định góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến. - Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông hoặc tính chất tam giác vuông cân tính chiều cao của lăng trụ. - Thể tích khối lăng trụ có chiều cao [h ], diện tích đáy [B ] là [V = Bh ]. 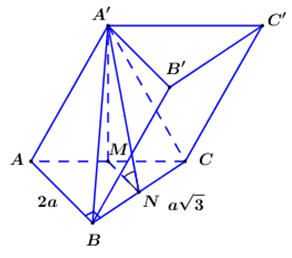Giải chi tiết: Gọi (M,{ mkern 1mu} N ) lần lượt là trung điểm của (AC,{ mkern 1mu} { mkern 1mu} BC ). Vì ( Delta ABC ) vuông tại (B ) nên (M ) là tâm đường tròn ngoại tiếp ( Delta ABC ), lại có (A'A = A'B = A'C ) nên hình chiếu vuông góc của (A' ) lên ( left( {ABC} right) ) trùng với tâm đường tròn ngoại tiếp ( Delta ABC ). ( Rightarrow A'M bot left( {ABC} right) ) Ta có: (MN ) là đường trung bình của ( Delta ABC Rightarrow MN//AB ). ( Rightarrow MN bot AC ) và (MN = frac{1}{2}AB = a ). Ta có: ( left { { begin{array}{*{20}{l}}{AC bot MN} {AC bot A'M} end{array}} right. Rightarrow AC bot left( {A'MN} right) Rightarrow AC bot A'N ) ( Rightarrow angle left( { left( {A'BC} right); left( {ABC} right)} right) = angle left( {A'N;MN} right) = angle A'NM = {45^0} ) ( Rightarrow Delta A'MN ) vuông cân tại (M ) ( Rightarrow A'M = MN = a ) Vậy ({V_{ABC.A'B'C'}} = A'M.{S_{ Delta ABC}} = A'M. frac{1}{2}AB.BC = a. frac{1}{2}.2a.a sqrt 3 = sqrt 3 {a^3} ).