Câu hỏi:

28/06/2022 186

Một hình nón đỉnh S, đáy là hình tròn tâm O, góc ở đỉnh bằng 120°. Trên đường tròn đáy lấy một điểm A cố định và điểm M di động. Có bao nhiêu vị trí của M để diện tích tam giác SAM đạt giá trị lớn nhất?

A. Có 1 vị trí

B. Có 2 vị trí

C. Có 3 vị trí

D. Có vô số vị trí

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra Học kì 1 Toán 12 có đáp án (Mới nhất) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Chọn B.

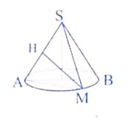
Một hình nón đỉnh S, đáy là hình tròn tâm O, góc ở đỉnh bằng 120°. Trên đường tròn đáy (ảnh 1)

Gọi H là hình chiếu vuông góc của M lên SA.

Ta có, diện tích ΔSAM được cho bởi:

$S = \frac{1}{2} S A . M H$ .

Do đó, diện tích ΔSAM đạt giá trị lớn nhất khi:

MH đạt giá trị lớn nhất ⇔ MH = MS

$\Leftrightarrow M S ⊥ S A$ .

Tức M là giao điểm của đường tròn đáy hình nón với mặt phẳng (P) qua S và vuông góc với SA.

Từ giả thiết

\hat{A S B} = 120 °

suy ra tồn tại điểm M trên đường tròn đáy thỏa mãn yêu cầu đề bài.

Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho một tờ giấy hình chữ nhật với chiều dài 12 cm và chiểu rộng 8cm. Gấp góc bên phải của tờ giấy sao cho sau khi gấp, đỉnh của góc đó chạm đáy dưới như hình vẽ. Để độ dài nếp gấp là nhỏ nhất thì giá trị nhỏ nhất đó bằng bao nhiêu?

A. $6 \sqrt{5}$

B. $6 \sqrt{2}$

C. 6

D. $6 \sqrt{3}$

Lời giải

Chọn D.

Đặt $E F = x, E C = 8 - x \Rightarrow F C = \sqrt{x^{2} - {(8 - x)}^{2}} = \sqrt{16 x - 64}$

Ta có

Δ A D F ~ Δ F C E (g . g) \Rightarrow \frac{E F}{A F} = \frac{C F}{A D} \Rightarrow

A F = \frac{E F . A D}{F C} = \frac{8 x}{\sqrt{16 x - 64}}

y = A E = \sqrt{A F^{2} + E F^{2}} = \sqrt{\frac{64 x^{2}}{16 x - 64} + x^{2}} = \sqrt{\frac{16 x^{3}}{16 x - 64}}

f (x) = \frac{16 x^{3}}{16 x - 64} x \in (0; 8)

;

f' (x) = \frac{48 x^{2} (16 x - 64) - 16.16 x^{3}}{{(16 x - 64)}^{2}}

f' (x) = 0 \Leftrightarrow 768 x^{3} - 3072 x^{2} - 256 x^{3} = 0 \Leftrightarrow 512 x^{3} - 3072 x^{2} = 0 \Leftrightarrow x = 6

BBT:

Cho một tờ giấy hình chữ nhật với chiều dài 12 cm và chiểu rộng 8cm. (ảnh 2)

y = \sqrt{f (x)} \Rightarrow y_{\min} = \sqrt{f_{\min}} = \sqrt{108} = 6 \sqrt{3}

Câu 2

Cho hàm số $y = a x^{3} + b x^{2} + c x + d$ có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng ?

A. $a < 0, b > 0, c > 0, d < 0$

B. $a < 0, b < 0, c > 0, d < 0$

C. $a > 0, b < 0, c < 0, d > 0$

D. $a < 0, b > 0, c < 0, d < 0$

Lời giải

Chọn A.

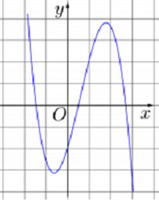
Dựa vào đồ thị hàm số $y = a x^{3} + b x^{2} + c x + d$ , ta có nhận xét sau

* Đồ thị hình chữ N ngược nên hệ số a < 0

* Ta có $y = a x^{3} + b x^{2} + c x + d \Rightarrow y' = 3 a x^{2} + 2 b c + c = 0 (*) \Rightarrow Δ'_{(*)} = b^{2} - 3 a c$

Đồ thị hàm số đi qua hai điểm cực trị có hoành độ $x_{1}, x_{2}$ trái dấu nhau nên

$\{\begin{cases} Δ'_{(*)} > 0 \\ x_{1} . x_{2} = \frac{c}{3 a} < 0 \end{cases} \Rightarrow c > 0$

* Dễ thấy $x_{1} + x_{2} = - \frac{2 b}{3 a} > 0 \Rightarrow b > 0$ và đồ thị hàm số cắt Ox tại ba điểm phân biệt nên d < 0

Câu 3

Cho hàm số $y = \frac{x^{2} - x + 4}{x - 1}$ . Tích các giá trị cực đại và cực tiểu của hàm số bằng:

A. -15

B. -10

C. -5

D. 0

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho biểu thức $P = \sqrt[4]{x . \sqrt[3]{x^{2} . \sqrt{x^{3}}}}$ , với x > 0. Mệnh đề nào dưới đây đúng ?

A. $P = x^{\frac{1}{2}}$

B. $P = x^{\frac{13}{24}}$

C. $P = x^{\frac{1}{4}}$

D. $P = x^{\frac{2}{3}}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hàm số $y = \frac{1}{3} x^{3} - (m + 1) x^{2} + m (m + 2) x + 2016$ . Tìm tất cả các giá trị m để hàm số đồng biến trên khoảng (3;7).

A. $m \leq 1$

B. $m < 1$

C. $m \geq 5$

D. $m \geq 5; m \leq 1$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số y = f(x) xác định trên $ℝ \ \{0\}$ , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình f(x) = m có ba nghiệm thực phân biệt.

A. [-1;2]

B. (-1;2)

C. (-1;2]

D. $(- \infty; 2]$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hàm số $y = x^{3} - 3 m x^{2} + 4 m^{3}$ với giá trị nào của m để hàm số có 2 điểm cực trị A và B sao cho $A B = \sqrt{20}$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Viên chức

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học