Câu hỏi:
01/07/2022 599
Cho hình nón có góc ở đỉnh bằng \({120^0}\) và đường cao bằng 2. Tính diện tích xung quanh của hình nón đã cho.
Cho hình nón có góc ở đỉnh bằng \({120^0}\) và đường cao bằng 2. Tính diện tích xung quanh của hình nón đã cho.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án B
Phương pháp giải:
- Sử dụng tính chất tam giác cân: Đường trung tuyến đồng thời là đường phân giác.
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính độ dài đường sinh \(l\) và bán kính đáy \(r\) của hình nón.
- Áp dụng công thức tính diện tích xung quanh của hình nón có độ dài đường sinh \(l\) và bán kính đáy \(r\) là \({S_{xq}} = \pi rl\).
Giải chi tiết:
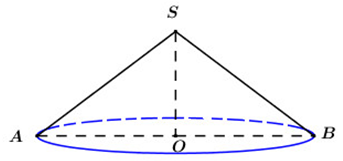
Gọi \(S\) là đỉnh hình nón, \(AB\) là 1 đường kính của hình nón và \(O\) là tâm đường tròn đáy của hình nón.
Khi đó ta có \(\angle ASB = {120^0}\) và \(h = SO = 2\).
Ta có: \(\Delta SAB\) cân tại \(S\) suy ra \(SO\) là phân giác của \(\angle ASB\).
\( \Rightarrow \angle ASO = \frac{1}{2}\angle ASB = {60^0}\)
Xét tam giác vuông \(SOA\) có: \(r = OA = SO.\tan {60^0} = 2\sqrt 3 \), \(l = SA = \frac{{SO}}{{\cos {{60}^0}}} = 4\)
Vậy diện tích xung quanh của hình nón là: \({S_{xq}} = \pi rl = \pi .2\sqrt 3 .4 = 8\sqrt 3 \pi \).
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(S = \frac{{937}}{{12}}\)
Phương pháp giải:
- Giải phương trình hoành độ giao điểm.
- Sử dụng công thức: Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),{\mkern 1mu} {\mkern 1mu} y = g\left( x \right)\), các đường thẳng \(x = a,{\mkern 1mu} {\mkern 1mu} x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Giải chi tiết:
Xét phương trình hoành độ giao điểm:
\( - {x^3} + 12x = - {x^2} \Leftrightarrow - {x^3} + {x^2} + 12x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 4}\\{x = - 3}\end{array}} \right.\)
Vậy diện tích của hình phẳng \(\left( H \right)\) là:
\(\int\limits_{ - 3}^0 {\left| { - {x^3} + {x^2} + 12x} \right|} + \int\limits_0^4 {\left| { - {x^3} + {x^2} + 12x} \right|} = \frac{{99}}{4} + \frac{{160}}{3} = \frac{{937}}{{12}}\).
Lời giải
Đáp án D
Phương pháp giải:
- Tìm hàm số vận tốc: \(v\left( t \right) = \int {a\left( t \right)dt} \), sử dụng dữ kiện \(v\left( 0 \right) = 15\) để tìm C.
- Quãng đường đi được sau 10 giây là: \(S = \int\limits_0^{10} {v\left( t \right)dt} \).
Giải chi tiết:
Ta có \(v = \int {a\left( t \right)dt = \int {\left( {3t - 8} \right)dt} } = \frac{{3{t^2}}}{2} - 8t + C\).
Vì ô tô đang chạy với vận tốc 15m/s nên ta có: \(v\left( 0 \right) = 15 \Rightarrow C = 15.\)
\( \Rightarrow v = \frac{{3{t^2}}}{2} - 8t + 15.\)
Vậy quãng đường ô tô đi được sau 10 giây là: \(S = \int\limits_0^{10} {\left( {\frac{{3{t^2}}}{2} - 8t + 15} \right)dt = 250} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận