Câu hỏi:
01/07/2022 2,289
Trong không gian cho hai điểm \[A,B\] cố định và độ dài đoạn thẳng \[AB\] bằng 4. Biết rằng tập hợp các điểm \[M\] sao cho \[MA = 3MB\] là một mặt cầu. Tìm bán kính \[R\] của mặt cầu đó?
Trong không gian cho hai điểm \[A,B\] cố định và độ dài đoạn thẳng \[AB\] bằng 4. Biết rằng tập hợp các điểm \[M\] sao cho \[MA = 3MB\] là một mặt cầu. Tìm bán kính \[R\] của mặt cầu đó?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án C
Giải chi tiết:
Gọi \(I\) là điểm thỏa mãn \(\overrightarrow {IA} = 9\overrightarrow {IB} \)
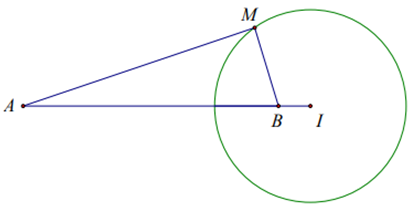
\(MA = 3MB \Leftrightarrow M{A^2} = 9M{B^2}\)
\( \Leftrightarrow {\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2} = 9{\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2}\)
\( \Leftrightarrow {\overrightarrow {MI} ^2} + 2\overrightarrow {MI} .\overrightarrow {IA} + {\overrightarrow {IA} ^2} = 9{\overrightarrow {MI} ^2} + 18\overrightarrow {MI} .\overrightarrow {IB} + 9{\overrightarrow {IB} ^2}\)
\( \Leftrightarrow - 8M{I^2} + 2\overrightarrow {MI} \left( {\overrightarrow {IA} - 9\overrightarrow {IB} } \right) = 9I{B^2} - I{A^2}\)
\( \Leftrightarrow M{I^2} = \frac{{I{A^2} - 9I{B^2}}}{8}\)
Dễ dàng tính được \(IA = \frac{9}{8}AB = \frac{9}{2}{\mkern 1mu} ;{\mkern 1mu} {\mkern 1mu} IB = \frac{1}{8}AB = \frac{1}{2}\)
\( \Rightarrow R = MI = \sqrt {\frac{{I{A^2} - 9I{B^2}}}{8}} = \sqrt {\frac{{{{\left( {\frac{9}{2}} \right)}^2} - {{\left( {\frac{1}{2}} \right)}^2}}}{8}} = \frac{3}{2}\).
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(S = \frac{{937}}{{12}}\)
Phương pháp giải:
- Giải phương trình hoành độ giao điểm.
- Sử dụng công thức: Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),{\mkern 1mu} {\mkern 1mu} y = g\left( x \right)\), các đường thẳng \(x = a,{\mkern 1mu} {\mkern 1mu} x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Giải chi tiết:
Xét phương trình hoành độ giao điểm:
\( - {x^3} + 12x = - {x^2} \Leftrightarrow - {x^3} + {x^2} + 12x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 4}\\{x = - 3}\end{array}} \right.\)
Vậy diện tích của hình phẳng \(\left( H \right)\) là:
\(\int\limits_{ - 3}^0 {\left| { - {x^3} + {x^2} + 12x} \right|} + \int\limits_0^4 {\left| { - {x^3} + {x^2} + 12x} \right|} = \frac{{99}}{4} + \frac{{160}}{3} = \frac{{937}}{{12}}\).
Lời giải
Đáp án D
Phương pháp giải:
- Tìm hàm số vận tốc: \(v\left( t \right) = \int {a\left( t \right)dt} \), sử dụng dữ kiện \(v\left( 0 \right) = 15\) để tìm C.
- Quãng đường đi được sau 10 giây là: \(S = \int\limits_0^{10} {v\left( t \right)dt} \).
Giải chi tiết:
Ta có \(v = \int {a\left( t \right)dt = \int {\left( {3t - 8} \right)dt} } = \frac{{3{t^2}}}{2} - 8t + C\).
Vì ô tô đang chạy với vận tốc 15m/s nên ta có: \(v\left( 0 \right) = 15 \Rightarrow C = 15.\)
\( \Rightarrow v = \frac{{3{t^2}}}{2} - 8t + 15.\)
Vậy quãng đường ô tô đi được sau 10 giây là: \(S = \int\limits_0^{10} {\left( {\frac{{3{t^2}}}{2} - 8t + 15} \right)dt = 250} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)