Câu hỏi:
12/07/2024 2,531
Vẽ đường cao xuất phát từ đỉnh B của tam giác vuông ABC (Hình 2a).
Vẽ đường cao xuất phát từ đỉnh F của tam giác tù DEF (Hình 2b).
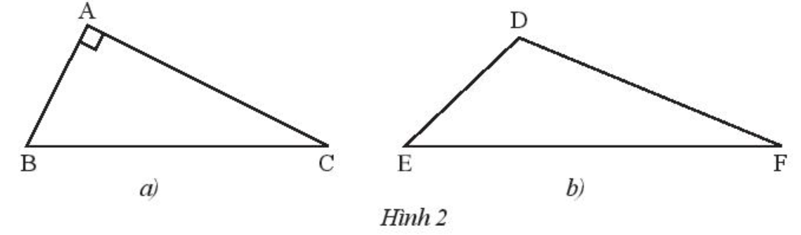
Vẽ đường cao xuất phát từ đỉnh B của tam giác vuông ABC (Hình 2a).
Vẽ đường cao xuất phát từ đỉnh F của tam giác tù DEF (Hình 2b).
Quảng cáo
Trả lời:
Giải bởi Vietjack
+) Hình 2a:
Tam giác ABC có là góc vuông nên BA AC.
Do đó đường cao xuất phát từ đỉnh B của tam giác vuông ABC là BA.
+) Hình 2b:
Tam giác DEF có là góc tù nên đường cao xuất phát từ đỉnh F của tam giác DEF nằm ngoài tam giác.
Ta thực hiện theo các bước sau:
Bước 1. Vẽ tam giác tù DEF.
Bước 2. Kéo dài cạnh DE về phía D.
Bước 3. Đặt êke sao cho một cạnh của êke trùng với đường thẳng DE, di chuyển êke sao cho đỉnh còn lại đi qua đỉnh F.
Bước 4. Khi đó kẻ một đoạn thẳng từ F đến cạnh DE thông qua cạnh của êke vừa đặt ở bước 2 ta thu được đoạn thẳng vuông góc từ đỉnh F đến cạnh DE.
Bước 5. Thực hiện đánh dấu chân đường vuông góc từ F đến DE và xóa các đoạn thừa, ta thu được đường cao FH của tam giác DEF như sau:
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 8 (chương trình mới) ( 120.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Tam giác BMC có BM = BC nên tam giác BMC cân tại B.
Tam giác BMC cân tại B, có BN là đường phân giác nên BN cũng là đường cao của tam giác BMC.
Do đó BN MC.
Tam giác BMC có CA BM, BN MC nên CA, BN là hai đường cao của tam giác BMC.
Mà CA và BN cắt nhau tại H nên H là trực tâm của tam giác BMC.
Do đó MH BC.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
-
Đề thi giữa học kì 2 Toán 7 KNTT - Đề 01 có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận