Câu hỏi:

05/07/2022 214

Một người thợ thủ công cần làm một cái thùng hình hộp đứng không nắp đáy là hình vuông có thể tích \[100{\mkern 1mu} c{m^3}\]. Để tiết kiệm vật liệu làm thùng, người đó cần thiết kế sao cho tổng S của diện tích xung quanh và diện tích mặt đáy là nhỏ nhất.

A. \[S = 30\sqrt[3]{{40}}.\]

B. \[S = 40\sqrt[3]{{40}}.\]

C. \[S = 10\sqrt[3]{{40}}.\]

D. \[S = 20\sqrt[3]{{40}}.\]

Xem lời giải

Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án A

Gọi cạnh đáy, cạnh bên của hình hộp đứng lần lượt là x và y (\(x,y > 0\))

Ta có: \(V = 100 \Rightarrow {x^2}y = 100 \Rightarrow y = \frac{{100}}{{{x^2}}}\). Khi đó: \(S = 4{\rm{x}}y + {x^2} = 4{\rm{x}}{\rm{.}}\frac{{100}}{{{x^2}}} + {x^2} = \frac{{400}}{x} + {x^2}\)

\( = \frac{{200}}{x} + \frac{{200}}{x} + {x^2} \ge 3\sqrt[3]{{\frac{{200}}{x}.\frac{{200}}{x}.{x^2}}} = 3\sqrt[3]{{{{4.10}^3}}} = 30\sqrt[3]{{40}}\).

Vậy S đạt giá trị nhỏ nhất bằng \(30\sqrt[3]{{40}}\) khi \(\frac{{200}}{x} = {x^2} \Leftrightarrow {x^3} = 200 \Leftrightarrow x = \sqrt[3]{{200}}\).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm nguyên hàm của hàm số \[f\left( x \right) = {\left( {3 - 5x} \right)^4}.\]

A. \[\int {f\left( x \right){\rm{d}}x = - \frac{{{{\left( {3 - 5x} \right)}^5}}}{5}} + C.\]

B. \[\int {f\left( x \right){\rm{d}}x = - \frac{{{{\left( {3 - 5x} \right)}^5}}}{{25}}} + C.\]

C. \[\int {f\left( x \right){\rm{d}}x = \frac{{{{\left( {3 - 5x} \right)}^5}}}{{25}}} + C.\]

D. \[\int {f\left( x \right){\rm{d}}x = - 20{{\left( {3 - 5x} \right)}^3}} + C.\]

Lời giải

Đáp án B

Ta có \(\int {f\left( x \right)d{\rm{x}}} = \int {{{\left( {3 - 5{\rm{x}}} \right)}^4}d{\rm{x}}} = \frac{1}{5}\int {{{\left( {5{\rm{x}} - 3} \right)}^4}d\left( {5{\rm{x}} - 3} \right)} = \frac{{\left( {5{\rm{x}} - {3^5}} \right)}}{{25}} + C\).

Câu 2

Tính diện tích S của phần hình phẳng gạch sọc (như hình vẽ bên dưới) giới hạn bởi đồ thị của hàm số bậc ba \[y = a{x^3} + b{x^2} + cx + d\] và trục hoành.

A. \[S = \frac{{31\pi }}{5}\]

B. \[S = \frac{{27}}{4}\]

C. \[S = \frac{{19}}{3}\]

D. \[S = \frac{{31}}{5}\]

Lời giải

Đáp án B

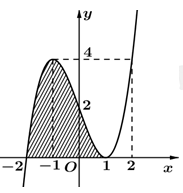
Dựa vào đồ thị suy ra \(y = a\left( {x + 2} \right){\left( {x - 1} \right)^2}\).

Do đồ thị hàm số đi qua điểm \(\left( {0;2} \right) \Rightarrow 2 = 2{\rm{a}} \Rightarrow a = 1\)

Khi đó \(S = \int\limits_{ - 2}^1 {\left( {x + 2} \right){{\left( {x - 1} \right)}^2}d{\rm{x}}} = \frac{{27}}{4}\).

Câu 3

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y = {x^3} - 3{x^2} + 4\] trên đoạn \[\left[ { - 1;3} \right]\]. Giá trị của biểu thức \[P = {M^2} - {m^2}\] là

A. 48.

B. 64.

C. 16.

D. −16.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình hình chiếu của đường thẳng \[d:\;\frac{{x + 3}}{2} = \frac{{y + 1}}{1} = \frac{z}{{ - 1}}\] trên mặt phẳng \[\left( P \right):\;x - 3y + 2z + 6 = 0?\]

A. \[\left\{ \begin{array}{l}x = 1 + 31t\\y = 1 + 5t\\z = - 2 - 8t\end{array} \right..\]

B. \[\left\{ \begin{array}{l}x = 1 - 31t\\y = 1 + 5t\\z = - 2 - 8t\end{array} \right..\]

C. \[\left\{ \begin{array}{l}x = 1 + 31t\\y = 3 + 5t\\z = - 2 - 8t\end{array} \right..\]

D. \[\left\{ \begin{array}{l}x = 1 + 31t\\y = 1 + 5t\\z = 2 - 8t\end{array} \right..\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \[\left( P \right):x + y - z - 2 = 0,\] \[\left( Q \right):x + 3y - 12 = 0\] đường thẳng \[d:\frac{{x - 1}}{3} = \frac{{y + 2}}{{ - 1}} = \frac{{z + 1}}{2}.\] Viết phương trình mặt phẳng \[\left( R \right)\] chứa đường thẳng d và giao tuyến của hai mặt phẳng \[\left( P \right),\left( Q \right).\]

A. \[\left( R \right):5x + y - 7z - 1 = 0.\]

B. \[\left( R \right):x + 2y - z + 2 = 0.\]

C. \[\left( R \right):x + 2y - z = 0.\]

D. \[\left( R \right):15x + 11y - 17z - 10 = 0.\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Một hình trụ có bán kính đáy và chiều cao đều bằng 4 dm. Một hình vuông ABCD có hai cạnh AB và CD lần lượt là các dây cung của hai đường tròn đáy. Biết mặt phẳng (ABCD) không vuông góc với mặt đáy của hình trụ. Tính diện tích S của hình vuông \[ABCD.\]

A. \[S = 20{\mkern 1mu} d{m^2}.\]

B. \[S = 40{\mkern 1mu} d{m^2}.\]

C. \[S = 80{\mkern 1mu} d{m^2}.\]

D. \[S = 60{\mkern 1mu} d{m^2}.\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hàm số \[y = f\left( x \right)\] có đạo hàm \[f'\left( x \right) = x{\left( {x - 1} \right)^2}\left( {3{x^4} + m{x^3} + 1} \right)\] với mọi \[x \in \mathbb{R}.\] Có bao nhiêu số nguyên âm m để hàm số \[g\left( x \right) = f\left( {{x^2}} \right)\] đồng biến trên khoảng \[\left( {0; + \infty } \right)?\]

A. 3

B. 4

C. 5

D. 6

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bình luận

Tìm nguyên hàm của hàm số \[f\left( x \right) = {\left( {3 - 5x} \right)^4}.\]

Tính diện tích S của phần hình phẳng gạch sọc (như hình vẽ bên dưới) giới hạn bởi đồ thị của hàm số bậc ba \[y = a{x^3} + b{x^2} + cx + d\] và trục hoành.

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y = {x^3} - 3{x^2} + 4\] trên đoạn \[\left[ { - 1;3} \right]\]. Giá trị của biểu thức \[P = {M^2} - {m^2}\] là

Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình hình chiếu của đường thẳng \[d:\;\frac{{x + 3}}{2} = \frac{{y + 1}}{1} = \frac{z}{{ - 1}}\] trên mặt phẳng \[\left( P \right):\;x - 3y + 2z + 6 = 0?\]

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu