Một người đi xe đạp từ A đến B với vận tốc 12 km/h. Khi từ B trở về A người đó đi theo con đường khác ngắn hơn con đường cũ là 5 km và vận tốc nhỏ hơn vận tốc lúc đi là 2 km/h. Tính chiều dài quãng đường AB lúc đi biết thời gian lúc đi ít hơn thời gian lúc về là 40 phút.
Câu hỏi trong đề: Đề kiểm tra giữa kì 2 Toán 8 có đáp án ( Mới nhất) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi x (km) là chiều dài quãng đường AB lúc đi (x > 0).
Chiều dài quãng đường tắt từ B về A ngắn hơn đường lúc đi 5 km là x – 5 (km).
Vận tốc lúc đi về từ B đến A nhỏ hơn vận tốc lúc đi là: 12 – 2 = 10 (km/h).
Thời gian người đi xe đạp đi hết quãng đường từ A đến B là:
tAB = (h).
Thời gian người đi xe đạp đi hết quãng đường tắt từ B về A là:
tBA = (h).
Đổi 40 phút = giờ.
Vì thời gian lúc đi từ A đến B ít hơn thời gian lúc đi từ B về A là 40 phút nên ta có phương trình:
Û 6x – 30 – 5x = 40
Û 6x – 5x = 40 + 30
Û x = 70 (thoản mãn)
Vậy chiều dài quãng đường AB lúc đi là 70 km.Đang tải chế độ Học...
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
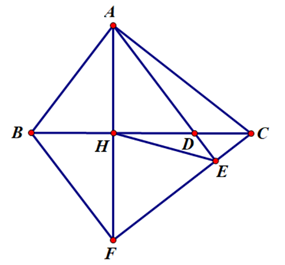
a) Xét ∆ABC và ∆HBA có:
(gt)
chung (gt)
Do đó ∆ABC ∆HBA (g.g);b) Xét ∆ADH và ∆CDE có:
= 90o (gt)
(hai góc đối đỉnh)
Do đó ∆ADH ∆CDE (g.g).
Suy ra (các cạnh tương ứng tỉ lệ)
Vậy: AH.CD = CE.AD (đccm)c) Ta có: ∆ADH ∆CDE (câu b)
Suy ra (các cạnh tương ứng tỉ lệ)
Xét ∆HDE và ∆ADC có:
(cmt)
(hai góc đối đỉnh)
Suy ra ∆HDE ∆ADC (c.g.c)
Suy ra (các cạnh tương ứng tỉ lệ)
Do đó HD.AC = AD.HE
Mặc khác H là trung điểm của BD (gt) ;
Suy ra: HD.AC = .AC = AD.HE
Vậy BD.AC = 2AD.HE.d) Vì AH vừa là đường cao vừa là trung tuyến của BD nên AH là trung trực của BD.
Suy ra ∆ADB cân tại A và AH là phân giác của hay .
Từ câu a: ∆ABC ∆HBA suy ra (hai góc tương ứng);
Từ câu b: ∆ADH ∆CDE suy ra (hai góc tương ứng).
Do đó hay CH là phân giác của .
Mặc khác HC vừa là đường cao của ∆ACF nên HC là trung trực của AF.
Hay BC là đường trung trực của đoạn thẳng AF.
Do đó BA = BF.
Suy ra ∆ABF cân tại B có .
Xét ∆BHF và ∆FEA có:
(cmt)
= 90o (gt)
Suy ra ∆BHF ∆FEA (g.g)
Suy ra (các cạnh tương ứng tỉ lệ).
Do đó BF.AE = HF.AF.
Vì H là trung trực AF nên .
Suy ra
Do đó AF2 = 2BF.AE (đpcm).
Lời giải
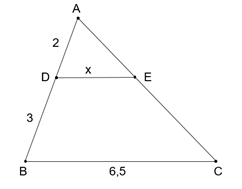
a) Theo hình vẽ ta có: AB = AD + DB = 2 + 3 = 5.
Áp dụng hệ quả định lý Ta – let trong ∆ABC có DE // BC, D Î AB, E Î AC ta có:
.
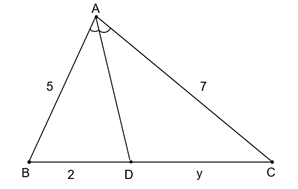
Vậy x = 2,6.b) Trong ∆ABC có AD là tia phân giác góc , D Î BC ta có:
Vậy y = 2,8.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập