✕

✨ Đăng kí VIP để truy cập không giới hạn. Đăng ký ngay

Câu hỏi:

14/07/2022 5,692

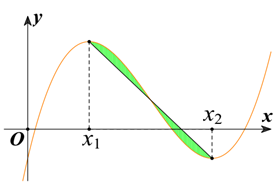
Cho hàm số bậc ba y = f (x) có đồ thị là đường cong (C) trong hình vẽ bên , biết hàm số f(x) đạt cực trị tại hai điểm x₁ , x₂ thỏa x₂ = x₁ + 4 và $f' (\frac{x_{1} + x_{2}}{2})$ = −12. Gọi d là đường thẳng đi qua hai điểm cực trị của đồ thị (C). Diện tích hình phẳng giới hạn bởi (C) và d bằng

A. 8

B. 4

C. 2

D. 1

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: A

Một hàm bậc ba nhận gốc tọa độ là điểm đối xứng thì y = ax³ + cx

Chọn x₁ = −2 thì x₂ = 2

Nên f(x) = x³ – 12x

Þ $\{\begin{matrix} f (2) = - 16 \\ f (- 2) = 16 \end{matrix}$

Đường thẳng đi qua A(2; −16) và B(−2; 16) nhận $\vec{u}$ = (−4; 32) = 4(−1; 8)

Þ d : −8(x – 2) – 1(y + 16) = 0 Û 8x + y = 0

Diện tích cần tìm là: 2S' = 2

\int_{- 2}^{0} [(x^{3} - 12 x + 8 x)] dx

= 2 . 4 = 8

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm họ nguyên hàm của hàm số f (x) = x³ ?

A. 4x⁴ + C

B. x⁴ + C

C. 3x² + C

D.

\frac{1}{4}

x⁴ + C

Lời giải

Đáp án đúng là: D

Ta có

\int x^{3} dx = \frac{x^{4}}{4} + C = \frac{1}{4} x^{4} + C .

Câu 2

Trong không gian Oxyz, mặt phẳng (P) đi qua A = (1; 0; 2) và song song với mặt phẳng (β) : 2x + 3y − z + 3 = 0 có phương trình là:

A. x + 2y – 3z + 5 = 0

B. 2x + 3y – z – 1 = 0

C. 2x + 3y – z = 0

D. 2x + 3y – z + 1 = 0

Lời giải

Đáp án đúng là: C

Do (P) // (β) nên vectơ của (β) là $\vec{n}$ = (2; 3; −1) cũng là vectơ pháp tuyến của (P)

Phương trình mặt phẳng (P) đi qua A(1; 0; 2) và có vectơ pháp tuyến là (2; 3; −1) là:

2(x – 1 ) + 3(y – 0) − 1(z − 2) = 0

Û 2x + 3y – z – 2 + 2 = 0 Û 2x + 3y – z = 0

Vậy (P): 2x + 3y – z = 0.

Câu 3

Trong không gian Oxyz, cho hai vectơ $\vec{a}$ = (1; −2; 3) và $\vec{b}$ = (2; 5; −1). Tọa độ của vectơ $2 \vec{a} - \vec{b}$ là

A. (3; 3; 2)

B. (0; −9; 7)

C. (4; 1; 5)

D. (−1; −7; 4)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hàm số f(x) = $\{\begin{matrix} e^{x} \\ x^{2} + 1 \end{matrix} \begin{matrix} khi \\ khi \end{matrix} \begin{matrix} x \leq 0 \\ x > 0 \end{matrix}$ liên tục trên R. Biết tích phân $\int_{- 1}^{2} f (x) dx = \frac{a}{b} + \frac{c}{e}$ với $\frac{a}{b}$ là phân số tối giản. Giá trị của tổng a + b + c bằng

A. 20

B. 21

C. 18

D. 19

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hàm số f(x) = xe^x biết F(x) là một nguyên hàm của f(x) và F(0) = 2. Khi đó F(x) bằng

A. F(x) = (x + 1)e^x + 3

B. F(x) = (x + 4)e^x – 2

C. F(x) = (x – 1)e^x + 3

D. F(x) = −e^x + 3

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong không gian Oxyz, cho hai điểm A(1; 3; −2) và B(3; −1; 0). Phương trình mặt cầu đường kính AB là

A. (x – 2)² + (y – 1)² + (z + 1)² =

\sqrt{6}

B. (x – 4)² + (y – 2)² + (z + 2)² = 24

C. (x – 2)² + (y – 1)² + (z – 1)² = 6

D. (x + 2)² + (y + 1)² + (z – 1)²= 6

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »