Câu hỏi:

16/01/2020 5,268

Biết rằng phương trình $\log_{2}^{2} x - \log_{2} (2018 x) - 2019 = 0$ có hai nghiệm thực $x_{1}, x_{2}$ Tích $x_{1} . x_{2}$ bằng

B. 0,5

C. 1

D. 2

Xem lời giải

Câu hỏi trong đề: 256 Bài tập Hàm số mũ và Logarit cực hay có lời giải chi tiết !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phương pháp

Sử dụng công thức

Đặt ẩn phụ rồi biến đổi để dử dụng hệ thức Vi-et.

Cách giải:

Ta có

Đặt ta có phương trình

Nhận thấy

Nên phương trình có hai nghiệm phân biệt t1; t2. Theo hệ thức Vi-ét ta có t1 + t2 = 1

Suy ra

Chọn D.

Chú ý: Phân biệt tích các nghiệm x, nhiều học sinh kết luận nhầm tích các nghiệm t.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tổng tất cả các nghiệm của phương trình $\log_{2} x . \log_{2} (32 x) + 4 = 0$ bằng:

A. .

B. .

C. .

D. .

Lời giải

Chọn D

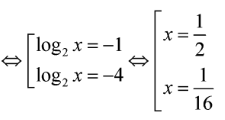
Tổng các nghiệm bằng

Câu 2

Tập nghiệm của phương trình $2 \log_{2} x = \log_{2} (2 - x)$ là:

Lời giải

Phương pháp:

Đưa về phương trình logarit dạng:

Cách giải:

ĐKXĐ:

Vậy, tập nghiệm của phương trình là: S = {1}.

Chọn B.

Chú ý:

Chú ý điều kiện xác định của hàm số logarit.

Câu 3

Tập nghiệm của bất phương trình $\log (x^{2} - 4 x + 5) > 1$ là

A. .

B. .

C. .

D. .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Có bao nhiêu giá trị nguyên của tham số m để tập nghiệm của bất phương trình $\ln (x^{2} + 2 x + m) - 2 \ln (2 x - 1) > 0$ chứa đúng hai số nguyên?

A. 10

B. 3

C. 4

D. 9

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho a, b là các số dương tùy ý, khi đó ln (a + ab) bằng

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Biết bất phương trình ${(\frac{2}{3})}^{x^{2} - x} \geq {(\frac{9}{4})}^{x - 1}$ có tập nghiệm là đoạn [a;b]. Tính b – a.

D. b – a = 2

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho phương trình $\log_{3}^{2} x - \log_{3} x + m - 3 = 0$ . Tìm tất cả các giá trị nguyên của tham số m

để phương trình đã cho có hai nghiệm phân biệt x1 < x2 thỏa mãn x2 – 81x1 < 0

A. 4

B. 5

C. 3

D. 6

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Biết rằng phương trình log22x-log2(2018x)-2019=0 có hai nghiệm thực x1,x2 Tích x1.x2 bằng

Tổng tất cả các nghiệm của phương trình log2x.log2(32x)+4=0 bằng:

Tập nghiệm của phương trình 2log2x=log2(2-x) là:

Tập nghiệm của bất phương trình log(x2-4x+5)>1 là

Có bao nhiêu giá trị nguyên của tham số m để tập nghiệm của bất phương trình ln(x2+2x+m)-2ln(2x-1)>0 chứa đúng hai số nguyên?

Cho a, b là các số dương tùy ý, khi đó ln (a + ab) bằng

Biết bất phương trình 23x2-x≥94x-1 có tập nghiệm là đoạn [a;b]. Tính b – a.

Cho phương trình log32x-log3x+m-3=0. Tìm tất cả các giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm phân biệt x1 < x2 thỏa mãn x2 – 81x1 < 0

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Biết rằng phương trình $\log_{2}^{2} x - \log_{2} (2018 x) - 2019 = 0$ có hai nghiệm thực $x_{1}, x_{2}$ Tích $x_{1} . x_{2}$ bằng

Tổng tất cả các nghiệm của phương trình $\log_{2} x . \log_{2} (32 x) + 4 = 0$ bằng:

Tập nghiệm của phương trình $2 \log_{2} x = \log_{2} (2 - x)$ là:

Tập nghiệm của bất phương trình $\log (x^{2} - 4 x + 5) > 1$ là

Có bao nhiêu giá trị nguyên của tham số m để tập nghiệm của bất phương trình $\ln (x^{2} + 2 x + m) - 2 \ln (2 x - 1) > 0$ chứa đúng hai số nguyên?

Biết bất phương trình ${(\frac{2}{3})}^{x^{2} - x} \geq {(\frac{9}{4})}^{x - 1}$ có tập nghiệm là đoạn [a;b]. Tính b – a.

Cho phương trình $\log_{3}^{2} x - \log_{3} x + m - 3 = 0$ . Tìm tất cả các giá trị nguyên của tham số m

để phương trình đã cho có hai nghiệm phân biệt x1 < x2 thỏa mãn x2 – 81x1 < 0