Cho 100 số thực, trong đó tích của ba số bất kì là một số âm. Chứng tỏ rằng tích của 100 số thực đó là một số dương.
Quảng cáo
Trả lời:
Lời giải:
Do trong 100 số thực đã cho thì tích của ba số bất kì là một số âm nên trong 100 số thực đó có ít nhất một số âm.
Ta gọi số âm đó là a.
Tách riêng số a, chia 99 số còn lại thành 33 nhóm, mỗi nhóm gồm 3 số.
Khi đó, tích của mỗi nhóm là một số âm.
Suy ra tích của 99 số trong 33 nhóm cũng là một số âm.
Do đó, tích của của số âm a và 99 số còn lại là một số dương.
Vậy tích của 100 số thực đã cho là một số dương.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
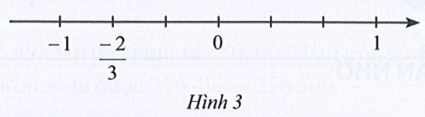
Trên trục số ở Hình 3 có các điểm −1; \(\frac{{ - 2}}{3}\); 0; 1.
Giá trị tuyệt đối của các số −1; \(\frac{{ - 2}}{3}\); 0; 1 lần lượt là 1; \(\frac{2}{3}\); 0; −1.
Ta biểu diễn giá trị tuyệt đối của các số −1; \(\frac{{ - 2}}{3}\); 0; 1 trên trục số như sau:
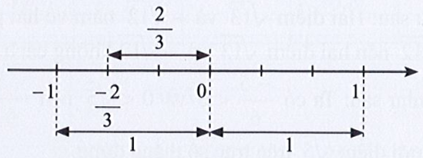
Lời giải
Lời giải:
Nhận xét: Với các số thực a, b, c, d, nếu a ≥ b, c ≥ d thì a + c ≥ b + d.
Ta có: |x – 2| ≥ 0 với mọi số thực x nên A = 10 . |x – 2| + 22 ≥ 22 với mọi số thực x.
Vậy giá trị nhỏ nhất của A là 22.
Dấu "=" xảy ra khi và chỉ khi |x – 2| = 0. Suy ra x – 2 = 0 hay x = 2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.