480 câu Trắc nghiệm tổng hợp Toán rời rạc có đáp án

Câu 1:

Cho 2 tập A, B rời nhau với | A | = 12 , | B | = 18 , | A ∪ B | | A | = 12 , | B | = 18 , | A ∪ B | là:

A. 12

B. 18

C. 29

D. 30

Xem đáp án

Câu 2:

Cho tập A={1,2,3,4,5,6,7,8,9}, tập B={1,2,3,9,10}. Tập A - B là:

A. {1,2,3,9}

B. {4,5,6,7,8}

C. {10}

D. {1,2,3,9,10}

Xem đáp án

Câu 3:

Cho 2 tập A, B với | A | = 13 , | B | = 19 , | A ∩ B | = 1. | A ∪ B | | A | = 13 , | B | = 19 , | A ∩ B | = 1. | A ∪ B | là:

A. 12

B. 31

C. 32

D. 18

Xem đáp án

Câu 4:

Cho 2 tập A, B với | A | = 15 , | B | = 20 , A ⊆ B . | A ∪ B | | A | = 15 , | B | = 20 , A ⊆ B . | A ∪ B | là:

A. 20

B. 15

C. 35

D. 5

Xem đáp án

Câu 5:

Cho biết số phần tử của tập A ∪ B ∪ C A ∪ B ∪ C nếu mỗi tập có 100 phần tử và các tập hợp đôi một rời nhau:

A. 200

B. 300

C. 100

D. 0

Xem đáp án

Câu 6:

Cho biết số phần tử của A ∪ B ∪ C A ∪ B ∪ C nếu mỗi tập có 100 phần tử và nếu có 50 phần tử chung của mỗi cặp 2 tập và có 10 phần tử chung của cả 3 tập.

A. 250

B. 200

C. 160

D. 150

Xem đáp án

Câu 7:

Cho X={1,2,3,4,5,6,7,8,9} A={1,2,3,8}, B={2,4,8,9}, C={6,7,8,9} Tìm xâu bit biểu diễn tập: ( A ∪ B ) ∩ C ( A ∪ B ) ∩ C

A. 000000011

B. 111111100

C. 000011

D. 111100

Xem đáp án

Câu 8:

Cho X={1,2,3,4,5,6,7,8,9}, A={1,2,3,8}. Tìm xâu bit biểu diễn tập

A. 111000010

B. 000111101

C. 111001101

D. 000110010

Xem đáp án

Câu 9:

Cho X={1,2,3,4,5,6,7,8,9}. Xâu bit biểu diễn tập A là: 111001011, xâu bit biểu diễn tập B là 010111001 Tìm xâu bit biểu diễn tập A ∪ B A ∪ B

A. 010001100

B. 101110010

C. 111111011

D. 010001101

Xem đáp án

Câu 10:

Cho tập A = {1,2,a}. Hỏi tập nào là tập lũy thừa của tập A?

A. {{1,2,a}}

B. { ∅ ∅ ,{1},{2},{a}}

C. { ∅ ∅ ,{1},{2},{a},{1,2},{1,a},{2,a},{1,2,a}}

D. {{1},{2},{a},{1,2},{1,a},{2,a},{1,2,a}}

Xem đáp án

Câu 11:

Xét các hàm từ R tới R, hàm nào là khả nghịch:

A.

f (x) = x^{2} - 4 x + 5

B.

f (x) = x^{4}

C.

f (x) = x^{3}

D.

f (x) = 6 - x^{2}

Xem đáp án

Câu 12:

Xét các hàm từ R tới R, hàm nào là khả nghịch:

A.

f (x) = x^{2} - 4 x + 5

`

B.

f (x) = x^{4}

C.

f (x) = x^{3}

D.

f (x) = 6 - x^{2}

Xem đáp án

Câu 13:

Cho quy tắc f: ℝ → ℝ thỏa mãn $f (x) = 2 x^{2} + 5$ . Khi đó f là:

A. Hàm đơn ánh.

B. Hàm toàn ánh

C. Hàm số

D. Hàm song ánh

Xem đáp án

Câu 14:

Cho hàm số $f (x) = 2 x$ và $g (x) = 4 x^{2} + 1$ , với x $\in$ ℝ . Khi đó g.f(-2) bằng:

A. 65

B. 34

C. 68

D. -65

Xem đáp án

Câu 15:

Cho tập A = {2, 3, 4, 5}. Hỏi tập nào KHÔNG bằng tập A?

A. {4, 3, 5, 2}

B. {a | a là số tự nhiên >1 và <6}

C. {b | b là số thực sao cho 1<b2 <36}

D. {2, 2, 3, 4, 4, 4, 5}

Xem đáp án

Câu 16:

Cho tập S = {a, b, c} khi đó số phần tử của tập lũy thừa của tập S là:

A. 3

B. 6

C. 8

D. 9

Xem đáp án

Câu 17:

Cho tập A = {a, b}, B = {0, 1, 2} câu nào dưới đây là SAI:

A. A x B = B x A.

B. |A x B| = |B x A|

C. |A x B| = |A| x |B|.

D. |A x B| = |B| x |A|.

Xem đáp án

Câu 18:

Cho 2 tập hợp:

A = {1,2,3,4,5,a, hoa, xe máy, dog, táo, mận}

B = {hoa, 3,4 , táo}

Tập nào trong các tập dưới đây là tập con của tập AxB:

A. {(1, táo), (a, 3), (3,3), (táo, a)}

B. {(hoa, hoa), (táo, mận), (5, 4)}

C. {(1,táo), (táo, táo), (xe máy, 3)}

D. Không có tập nào trong các tập trên

Xem đáp án

Câu 19:

Cho 2 tập A={1, 2, 3}, B={a, b, c, 2}. Trong số các tập dưới đây, tập nào là một quan hệ 2 ngôi từ A tới B?

A. {(1,a), (1,1), (2,a)}

B. {(2, 2), (2,3), (3,b)}

C. {(1,2), (2,2), (3,a)}

D. {(2,c), (2,2), (b,3)}

Xem đáp án

Câu 20:

Xác định tập lũy thừa của tập A={ôtô, Lan}

A. {{ôtô}, {Lan}, {táo}}

B. {{ôtô}, {Lan}, {ôtô, Lan}}

C. {{ôtô}, {Lan}, { ϕ ϕ }}

D. {{ôtô}, {Lan}, ϕ ϕ , {ôtô, Lan}}

Xem đáp án

Câu 21:

Xác định tích đề các của 2 tập A={1,a} và B={1,b}:

A. {(1,b), (a,b)}

B. {(1,1), (1,b), (a,1), (a,b)}

C. {(1,1), (1,b), ( ϕ ϕ ,1), ( ϕ ϕ ,b), (a,b)}

D. {(1,1), (1,b), (a,b), ϕ ϕ }

Xem đáp án

Câu 22:

Cho 2 tập C, D với | C | = 28 , | D | = 32 , | C ∩ D | = 4. | C ∪ D | | C | = 28 , | D | = 32 , | C ∩ D | = 4. | C ∪ D | là:

A. 4

B. 60

C. 52

D. 56

Xem đáp án

Câu 23:

Cho tập A = {1, 2, 3, 4, 5, 6, 7}, tập B = {2, 3, 8, 1, 7, 9}. Tập ( A − B ) ∪ ( B − A ) ( A − B ) ∪ ( B − A ) là:

A. {1,2,3,7}

B. {1,2,3,4,5,6,7,8,9}

C. Φ Φ

D. {4, 5, 6, 8, 9}

Xem đáp án

Câu 24:

Cho 2 tập A, B với A = {1,a,2,b,3,c,d}, B = {x,5,y,6,c,1,z}. Số phần tử của tập (A – B) là:

A. 0

B. 5

C. {a,2,b,3,d}

D. Φ Φ

Xem đáp án

Câu 25:

Cho 2 tập A, B với | A | = 100 , | B | = 200 , A ⊆ B . | A ∪ B | | A | = 100 , | B | = 200 , A ⊆ B . | A ∪ B | là:

A. 50

B. 100

C. 300

D. 200

Xem đáp án

Câu 26:

Cho biết số phần tử của tập A ∩ ( B ∪ C ) A ∩ ( B ∪ C ) nếu mỗi tập có 50 phần tử và các tập hợp đôi một rời nhau.

A. 50

B. 100

C. 0

D. 150

Xem đáp án

Câu 27:

Cho biết số phần tử của A ∩ ( B ∪ C ) A ∩ ( B ∪ C ) nếu mỗi tập có 100 phần tử và nếu có 50 phần tử chung của mỗi cặp 2 tập và có 10 phần tử chung của cả 3 tập.

A. 50

B. 90

C. 100

D. 10

Xem đáp án

Câu 28:

Cho X = {1,2,3,4,5,6,7,8,9} A = {1,2,3,8}, B = {2,4,8,9}, C = {6,7,8,9}. Tìm xâu bit biểu diễn tập: ( A ∩ B ) ∪ C ( A ∩ B ) ∪ C

A. 000000011

B. 010001111

C. 000011000

D. 111100111

Xem đáp án

Câu 29:

Cho X = {1,2,3,4,5,6,7,8,9}, A = {1,4,5,8,9} Tìm xâu bit biểu diễn tập $\bar{A}$ trên X:

A. 111000010

B. 000111101

C. 100110011

D. 011001100

Xem đáp án

Câu 30:

Cho X = {1,2,3,4,5,6,7,8,9}. Xâu bit biểu diễn tập A là: 111001011, xâu bit biểu diễn tập B là 010111001. Tìm xâu bit biểu diễn tập A ∩ B . A ∩ B .

A. 010001100

B. 101110010

C. 010001001

D. 010001101

Xem đáp án

Câu 31:

Cho tập A = {a,b,5}. Hỏi tập nào là tập lũy thừa của tập A?

A. {{5,a,b}}

B. { ∅ ∅ ,{a},{b},{5}}

C. {{a},{b},{5},{a,b},{a,5},{b,5},{a,b,5}}

D. { ∅ ∅ ,{a},{b},{5},{a,b},{a,5},{5,b},{5,b,a}}

Xem đáp án

Câu 32:

Xét các hàm từ R tới R, hàm nào dưới đây là khả nghịch:

A.

f (x) = x^{2} - 2 x + 1

B.

f (x) = x^{4} + x^{2} + 1

C.

f (x) = x^{4} + 2 x^{3} + x^{2}

D.

f (x) = 6 - x

Xem đáp án

Câu 33:

Cho hàm số $f (x) = 2 x$ và $g (x) = 4 x^{2} + 1$ , với x $\in$ ℝ . Khi đó f.g(-2) bằng:

A. 65

B. 34

C. 68

D. -65

Xem đáp án

Câu 34:

Cho tập A = {1, 2, 3, {a,4}, {a,b,c}, ∅ ∅ }. Lực lượng của A bằng:

A. 6

B. 5

C. 7

D. 8

Xem đáp án

Câu 35:

Cho tập S = {a, b, c,d} khi đó số phần tử của tập lũy thừa của tập S là:

A. 4

B. 16

C. 8

D. 9

Xem đáp án

Câu 36:

Cho 2 tập hợp: A= {1,2,3,4,5,a, hoa, xe máy, dog, táo, mận} B = {hoa, 3,4 , táo} Tập nào trong các tập dưới đây là tập con của tập BxA:

A. {(1, táo), (a, 3), (3,3), (táo, a)}

B. {(hoa, hoa), (táo, mận), (5, 4)}

C. {(1,táo), (táo, táo), (xe máy, 3)}

D. {(hoa,2), (táo,táo), (4,5)}

Xem đáp án

Câu 37:

Cho 2 tập A={1, 2, 3}, B={a, b, c, 2}. Trong số các tập dưới đây, tập nào là một quan hệ 2 ngôi từ A tới B?

A. {(1,a), (3,3), (2,a)}

B. {(2,2), (2,c), (3,b)}

C. {(1,a), (2,2), (3,1)}

D. {(2,c), (2,2), (b,3)}

Xem đáp án

Câu 38:

Xác định tập lũy thừa của tập A = {toán, văn}.

A. {{toán}, {văn}}

B. {{toán}, {văn}, Ф}

C. {{toán}, {văn}, {toán, văn}, Ф}

D. {{toán}, {văn}, {toán, văn}}

Xem đáp án

Câu 39:

Xác định tích đề các của 2 tập A = {9,x,y} và B = {9,a}:

A. {(9,a), (x,9),(y,9),(x,a),(y,a),(9,9)}

B. {(9,x), (9,y), (9,9), (a,9),(a,x),(a,y)}

C. {(9,x), (9,a), (x,a), (y,a), (x,9),(y,9)}

D. {(x,9), (a,9),(y,9),(x,a),(y,a),(9,9)}

Xem đáp án

Câu 40:

Số các xâu nhị phân có độ dài là 10 là:

A. 1024

B. 1000

C. 20

D. 10

Xem đáp án

Câu 41:

Số các xâu nhị phân có độ dài nhỏ hơn hoặc bằng 10 là:

A. 1024

B. 2048

C. 2046

D. 1022

Xem đáp án

Câu 42:

Số hàm từ tập A có k phần tử vào tập B có n phần tử là:

A. nk

B. (n-k)!

C. kn

D. (n!/k!)

Xem đáp án

Câu 43:

Có bao nhiêu xâu nhị phân độ dài là 8 hoặc bắt đầu bởi 00 hoặc kết thúc bởi 11.

A. 112

B. 128

C. 64

D. 124

Xem đáp án

Câu 44:

Có bao nhiêu xâu nhị phân độ dài bằng 8 và không chứa 6 số 0 liên tiếp.

A. 246

B. 248

C. 256

D. 254

Xem đáp án

Câu 45:

Có bao nhiêu xâu nhị phân độ dài bằng 8 bắt đầu bởi 00 và kết thúc bởi 11.

A. 64

B. 16

C. 32

D. 128

Xem đáp án

Câu 46:

Một sinh viên phải trả lời 8 trong số 10 câu hỏi cho một kỳ thi. Sinh viên này có bao nhiêu sự lựa chọn nếu sinh viên phải trả lời ít nhất 4 trong 5 câu hỏi đầu tiên?

A. 35

B. 75

C. 25

D. 20

Xem đáp án

Câu 47:

Cho tập A = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19} hỏi ta cần lấy ít nhất bao nhiêu phần tử từ tập A để chắc chắn rằng có một cặp có tổng bằng 20.

A. 6

B. 7

C. 8

D. 9

Xem đáp án

Câu 48:

Có 12 sinh viên trong một lớp học. Có bao nhiêu cách để 12 sinh viên làm 3 đề kiểm tra khác nhau nếu mỗi đề có 4 sinh viên làm. (Chính là số các cách chia 12 sinh viên làm 3 nhóm, mỗi nhóm 4 SV)

Số cách chọn 4 SV làm đề 1 là: C(4,12)

Số cách chọn 4 SV làm đề 2 là: C(4,8)

Số cách chọn 4 SV làm đề 3 là:C(4,4)

Vậy có C(4,12)xC(4,8)xC(4,4)=34650)

A. 220

B. 3465

C. 34650

D. 650

Xem đáp án

Câu 49:

Một dãy XXXYYY độ dài 6. X có thể gán bởi một chữ cái. Y có thể gán một chữ số. Có bao nhiêu dãy được thành lập theo cách trên:

A. 108

B. 1000000

C. 17576

D. 17576000

Xem đáp án

Câu 50:

Một phiếu trắc nghiệm đa lựa chọn gồm 10 câu hỏi. Mỗi câu có 4 phương án trả lời. Có bao nhiêu cách điền một phiếu trắc nghiệm nếu mọi câu hỏi đều được trả lời.

A. 410

B. 104

C. 40

D. 210

Xem đáp án

Câu 51:

Một phiếu trắc nghiệm đa lựa chọn gồm 10 câu hỏi. Mỗi câu có 4 phương án trả lời. Có bao nhiêu cách điền một phiếu trắc nghiệm nếu câu hỏi có thể bỏ trống.

A. 410

B. 510

C. 40

D. 50

Xem đáp án

Câu 52:

Kết quả của một cuộc điều tra ở Hà Nội cho thấy 96% các gia đình có máy thu hình, 98% có điện thoại và 95% có điện thoại và máy thu hình. Tính tỷ lệ % các gia đình ở Hà Nội không có thiết bị nào là). ( Tỷ lệ % các gia đình có điện thoại hoặc máy thu hình là 98%+96%-95%=99%. Tỷ lệ % các gia đình không có điện thoại và không có máy thu hình là 1%)

A. 4%

B. 5%

C. 1%

D. 2%

Xem đáp án

Câu 53:

Trong lớp CNTT có 50 sinh viên học tiếng Anh; 20 sinh viên học tiếng Pháp và 10 sinh viên học cả Anh và Pháp. Cho biết sĩ số của lớp là 80. Hỏi có bao nhiêu sinh viên không học tiếng Anh, Pháp.

A. 0

B. 5

C. 10

D. 20

Xem đáp án

Câu 54:

Cho tập A gồm 10 phần tử. Số tập con của tập A là:

A. 10

B. 100

C. 1024

D. 1000

Xem đáp án

Câu 55:

Mỗi người sử dụng thẻ ATM đều có mật khẩu dài 4 hoặc 6 ký tự. Trong đó mỗi ký tự là một chữ số. Hỏi có bao nhiêu mật khẩu?

A. 10000

B. 1010000

C. 410+610

D. 1110000

Xem đáp án

Câu 56:

Có bao nhiêu số nguyên dương không lớn hơn 1000 chia hết cho 7 hoặc 11?

A. 220

B. 200

C. 142

D. 232

Xem đáp án

Câu 57:

Có bao nhiêu số nguyên dương không lớn hơn 1000 không chia hết cho 7 hoặc 11.

A. 220

B. 780

C. 768

D. 1768

Xem đáp án

Câu 58:

Có 8 đội bóng thi đấu vòng tròn. Hỏi phải tổ chức bao nhiêu trận đấu?

A. 64

B. 56

C. 28

D. 32

Xem đáp án

Câu 59:

Một tập hợp 100 phần tử có bao nhiêu tập con có ít hơn ba phần tử?

A. 2100

B. 5050

C. 297

D. 5051

Xem đáp án

Câu 60:

Một tập hợp 100 phần tử có bao nhiêu tập con có 2 phần tử?

A. 298

B. 4950

C. 50

D. 9900

Xem đáp án

Câu 61:

Có 20 vé số khác nhau trong đó có 3 vé chứa các giải Nhất, Nhì, Ba. Hỏi có bao nhiêu cách trao giải thưởng cho 20 người, mỗi người giữ một vé?

A. 1140

B. 8000

C. 2280

D. 6840

Xem đáp án

Câu 62:

Một tổ bộ môn có 10 nam và 15 nữ. Có bao nhiêu cách chọn một hội đồng gồm 6 ủy viên, trong đó số ủy viên nam gấp đôi số ủy viên nữ?

A. 22050

B. 315

C. 54600

D. 575

Xem đáp án

Câu 63:

Công thức nào sau đây đúng. Cho n là số nguyên dương, khi đó $\sum_{k = 0}^{n} C (n, k)$ là:

A. 2n-1

B. 2n

C. 2n+1

D. 2n -1

Xem đáp án

Câu 64:

Công thức nào sau đây đúng. Cho n và k là các số nguyên dương với n ≥ k. Khi đó:

A. C ( n + 1 , k ) = C ( n , k − 1 ) + C ( n , k ) C ( n + 1 , k ) = C ( n , k − 1 ) + C ( n , k )

B. C ( n + 1 , k ) = C ( n − 1 , k ) + C ( n − 1 , k − 1 ) C ( n + 1 , k ) = C ( n − 1 , k ) + C ( n − 1 , k − 1 )

C. C ( n + 1 , k ) = C ( n , k ) + C ( n − 1 , k ) C ( n + 1 , k ) = C ( n , k ) + C ( n − 1 , k )

D. C (n + 1 , k) = C (n − 1 , k − 1) + C (n , k − 1) C (n + 1 , k) = C (n − 1 , k − 1) + C (n , k − 1)

Xem đáp án

Câu 65:

Hệ số của x¹²y¹³ trong khai triển (x+y)²⁵ là:

A. 25!

B.

\frac{25!}{12! 13!}

C.

\frac{13!}{12!}

D.

\frac{25!}{13!}

Xem đáp án

Câu 66:

Cho n, r là các số nguyên không âm sao cho r ≤ n r ≤ n . Khi đó:

A. C(n, r)=C(n+r-1, r)

B. C(n, r)=C(n, r-1)

C. C(n, r)=C(n, n-r)

D. C(n, r)=C(n-r, r)

Xem đáp án

Câu 67:

Trong khai triển (x+y)²⁰⁰ có bao nhiêu số hạng?

A. 100

B. 101

C. 200

D. 201

Xem đáp án

Câu 68:

Tìm hệ số của x⁹ trong khai triển của (2 - x)²⁰

A. C(20,10).210

B. (20,9).211

C. – C(20,9)211

D. – C(20,10)29

Xem đáp án

Câu 69:

Có bao nhiêu cách tuyển 5 trong số 10 cầu thủ của một đội quần vợt để đi thi đấu tại một trường khác?

A. 252

B. 250

C. 120

D. 30240

Xem đáp án

Câu 70:

Có bao nhiêu khả năng có thể xảy ra đối với các vị trí thứ nhất, thứ nhì và thứ ba trong cuộc đua có 12 con ngựa, nếu mọi thứ tự tới đích đều có thể xảy ra?

A. 220

B. 1320

C. 123

D. 312

Xem đáp án

Câu 71:

Có bao nhiêu số tự nhiên có 3 chữ số khác nhau được tạo từ tập các chữ số {1,3,5,7,9}.

A. 30

B. 60

C. 90

D. 120

Xem đáp án

Câu 72:

Có bao nhiêu số tự nhiên có 3 chữ số được tạo từ tập các chữ số {1,3,5,7,9}.

A. 125

B. 60

C. 65

D. 120

Xem đáp án

Câu 73:

Có bao nhiêu số lẻ có 3 chữ số được tạo từ tập các chữ số {0,1,2,3,4,5}.

A. 48

B. 60

C. 90

D. 75

Xem đáp án

Câu 74:

Trong một khoa có 20 sinh viên xuất sắc về Toán và 12 sinh viên xuất sắc về CNTT. Hỏi có bao nhiêu cách lựa chọn hai đại diện sao cho một là sinh viên Toán, một là sinh viên CNTT?

A. 20

B. 12

C. 32

D. 240

Xem đáp án

Câu 75:

Có bao nhiêu xâu nhị phân có độ dài bằng 5 mà hoặc có 2 bít đầu tiên là 0 hoặc có 2 bít cuối cùng là 1?

A. 16

B. 14

C. 2

D. 32

Xem đáp án

Câu 76:

Mỗi thành viên trong câu lạc bộ Toán tin có quê ở 1 trong 20 tỉnh thành. Hỏi cần phải tuyển bao nhiêu thành viên để đảm bảo có ít nhất 5 người cùng quê?

A. 81

B. 99

C. 101

D. 90

Xem đáp án

Câu 77:

Có bao nhiêu hàm số khác nhau từ tập có 4 phần tử đến tập có 3 phần tử:

A. 81

B. 64

C. 4

D. 12

Xem đáp án

Câu 78:

Số xâu nhị phân độ dài 4 có bít cuối cùng bằng 1 là:

A. 8

B. 12

C. 16

D. A, B và C đều sai

Xem đáp án

Câu 79:

Một quan hệ hai ngôi R trên một tập hợp X (khác rỗng) được gọi là quan hệ tương đương nếu và chỉ nếu nó có 3 tính chất sau:

A. Phản xạ – Đối xứng – Bắc cầu

B. Phản xạ – Phản đối xứng – Bắc cầu

C. Đối xứng – Phản đối xứng – Bắc cầu

D. Phản xạ – Đối xứng – Phản đối xứng.

Xem đáp án

Câu 80:

Một quan hệ hai ngôi R trên một tập hợp X (khác rỗng) được gọi là quan hệ thứ tự nếu và chỉ nếu nó có 3 tính chất sau:

A. Phản xạ – Đối xứng – Bắc cầu

B. Phản xạ – Phản đối xứng – Bắc cầu

C. Đối xứng – Phản đối xứng – Bắc cầu

D. Phản xạ – Đối xứng – Phản đối xứng.

Xem đáp án

Câu 81:

Cho biết quan hệ nào là quan hệ tương đương trên tập {0, 1, 2, 3}:

A. {(0,0),(1,1),(2,2),(3,3),(0,1),(0,2),(0,3)}

B. {(0,0),(1,1),(2,2),(3,3),(0,1),(1,0)}

C. {(0,0),(0,2),(2,0),(2,2),(2,3),(3,2),(3,3)}

D. {(0,0),(1,1),(1,3),(2,2),(2,3),(3,1),(3,2),(3,3)}

Xem đáp án

Câu 82:

Cho A ={1, 2, 3, 4, 5}. Quan hệ R được xác định: ∀ a , b ∈ A , a R b ⇔ a + b = 2 k ( k = 1 , 2 , . . . ) ∀ a , b ∈ A , a R b ⇔ a + b = 2 k ( k = 1 , 2 , . . . ) . Quan hệ R được biểu diễn là:

A. {(1,1),(2,2),(3,3),(4,4), (1,3),(3,1),(1,5),(5,1), (2,4),(4,2)}

B. {(1,1),(2,2),(3,3),(4,4),(5,5),(1,3),(1,5), (3,5), (2,4)}

C. {(1,1),(2,2),(3,3),(4,4),(5,5),(1,3),(3,1),(1,5),(5,1), (3,5), (5,3),(2,4),(4,2)}

D. {(1,3),(3,1),(1,5),(5,1), (3,5), (5,3),(2,4),(4,2)}

Xem đáp án

Câu 83:

Cho A={1,2,3,4,5}. Trên A xác định quan hệ R như sau: ∀ a , b ∈ A , a R b ⇔ a + b = 2 k + 1 ( k = 1 , 2 , . . . ) ∀ a , b ∈ A , a R b ⇔ a + b = 2 k + 1 ( k = 1 , 2 , . . . ) . Quan hệ R được biểu diễn là:

A. {(1,2),(1,4),(2,3),(2,5)}

B. {(1,1),(2,2),(3,3),(4,4),(5,5), (1,2),(1,4),(2,3),(2,5)}

C. {(1,2),(2,1),(1,4),(4,1), (2,5), (5,2)}

D. {(1,2),(2,1),(1,4),(4,1), (2,5), (5,2),(3,4),(4,3),(2,3),(3,2),(4,5),(5,4)}

Xem đáp án

Câu 84:

Cho tập A ={1,2,3,4,5}. Cho A1 = {1}, A2 ={2,3}, A3 = {4,5}. Quan hệ tương đương R trên A sinh ra phân hoạch A1, A2, A3 là:

A. {(1,1),(2,3),(4,5),(2,2),(3,3), (3,2),(4,4),(5,5),(5,4)}

B. {(1,1),(2,2),(3,3),(4,4),(5,5), (1,2),(1,3),(1,4),(1,5)}

C. {(1,1),(2,3),(3,2),(4,5), (5,4)}

D. {(2,2),(2,3),(3,2),(3,3), (4,4), (4,5),(5,4),(5,5), (1,1),(1,2),(2,1),(1,3),(3,1)}

Xem đáp án

Câu 85:

Cho tập A ={1,2,3,4,5,6}. Cho A1 = {1,2}, A2 = {3,4}, A3 = {5,6}. Quan hệ tương đương R trên A sinh ra phân hoạch A1, A2, A3 là:

A. {(1,1),(2,3),(4,5),(2,2),(3,3), (3,2),(4,4),(5,5),(5,4),(6,6),(5,6),(6,5)}

B. {(1,1),(2,2),(3,3),(4,4),(5,5), (6,6),(1,2),(2,1),(3,4),(4,3),(5,6),(6,5)}

C. {(1,1),(1,2),(2,2),(3,4), (3,3),(5,6),(4,4),(5,5),(6,6)}

D. {(2,2),(2,3),(1,1),(3,3), (4,4), (3,4),(4,3),(2,1), (1,1),(1,2),(2,1),(5,6),(6,5)}

Xem đáp án

Câu 86:

Cho tập A={1,2,3,4,5} và quan hệ tương đương R trên A như sau: R={(1,1),(2,2),(3,3),(4,4),(5,5),(2,4),(4,2)}. Xác định phân hoạch do R sinh ra:

A. A1 = {1,3,5}, A2 = {2,4}

B. A1 = {1}, A2 = {2,4}, A3 = {3,5}

C. A1 = {1}, A2 = {2,4}, A3 = {3}, A4 = {5}

D. A1 = {1,2}, A2 = {3,4}, A3 = {5}

Xem đáp án

Câu 87:

Cho A ={1, 2, 3, 4, 5}. Quan hệ R được xác định: ∀ a , b ∈ A , a R b ⇔ a + b = 2 k ( k = 1 , 2 , . . . ) ∀ a , b ∈ A , a R b ⇔ a + b = 2 k ( k = 1 , 2 , . . . ) . Xác định phân hoạch do R sinh ra:

A. A1 = {1,3}, A2 = {2,4}, A3 = {5}

B. A1 = {1}, A2 = {2,4}, A3 = {3}, A4 = {5}

C. A1 = {1}, A2 = {2}, A3 = {3}, A4 = {4}, A5 = {5}

D. A1 = {1,3,5}, A2 = {2,4}

Xem đáp án

Câu 88:

Một sinh viên phải trả lời 20 câu hỏi cho một kỳ thi, mỗi câu hỏi có 4 phương án trả lời. Biết rằng sinh viên bắt buộc phải lựa chọn phương án nào đó cho 10 câu hỏi đầu tiên, còn 10 câu hỏi sau câu trả lời có thể bỏ trống. Hỏi sinh viên này có bao nhiêu sự lựa chọn?

A. 430

B. 410+510

C. 2010

D. 304 + 1

Xem đáp án

Câu 89:

Có bao nhiêu xâu nhị phân độ dài bằng 10 bắt đầu bởi 11 và kết thúc bởi 00.

A. 64

B. 128

C. 256

D. 1024

Xem đáp án

Câu 90:

Có bao nhiêu xâu nhị phân độ dài bằng 6 và chứa 4 số 0 liên tiếp.

A. 4

B. 8

C. 10

D. 12

Xem đáp án

Câu 91:

Có bao nhiêu xâu nhị phân độ dài là 10 bắt đầu bởi 00.

A. 112

B. 128

C. 64

D. 256

Xem đáp án

Câu 92:

Số hàm từ tập A có 5 phần tử vào tập B có 4 phần tử là:

A. 1024

B. 625

C. 5

D. 20

Xem đáp án

Câu 93:

Số các xâu nhị phân có độ dài nhỏ hơn hoặc bằng 8 là:

A. 1024

B. 512

C. 510

D. 1022

Xem đáp án

Câu 94:

Số các xâu nhị phân có độ dài là 8 là:

A. 1024

B. 256

C. 16

D. 8

Xem đáp án

Câu 95:

Trong 100 người có ít nhất mấy người cùng tháng sinh?

A. 10

B. 9

C. 8

D. 7

Xem đáp án

Câu 96:

Cần phải có tối thiểu bao nhiêu sinh viên ghi tên vào lớp Toán rời rạc để chắc chắn sẽ có ít nhất 6 sinh viên đạt cùng một điểm thi nếu thang điểm gồm 5 bậc?

A. 30

B. 25

C. 26

D. 27

Xem đáp án

Câu 97:

Một dãy XXYYY độ dài 4. X có thể gán bởi một chữ số. Y có thể gán một chữ cái. Có bao nhiêu dãy được thành lập theo cách trên.

A. 102 x 263

B. 102 +263

C. 103 x 262

D. 103 + 262

Xem đáp án

Câu 98:

Mỗi sinh viên trong lớp K38CNTT của khoa Công nghệ đều có quê ở một trong 61 tỉnh thành trong cả nước. Cần phải tuyển bao nhiêu sinh viên để đảm bảo trong lớp K38CNTT có ít nhất 2 sinh viên cùng quê?

A. 62

B. 122

C. 123

D. 61

Xem đáp án

Câu 99:

Cần phải tung một con xúc xắc bao nhiêu lần để có một mặt xuất hiện ít nhất 3 lần?

A. 12

B. 13

C. 18

D. 19

Xem đáp án

Câu 100:

Cần tuyển chọn tối thiểu ra bao nhiêu người để chắc chắn có ít nhất 2 người có cùng ngày sinh trong năm 2016?

A. 365

B. 366

C. 367

D. 368

Xem đáp án

Câu 101:

Trong lớp CNTT có 45 sinh viên học tiếng Anh; 25 sinh viên học tiếng Pháp và 5 sinh viên không học môn nào. Cho biết sĩ số của lớp là 60. Hỏi có bao nhiêu sinh viên học cả tiếng Anh, Pháp.

A. 5

B. 10

C. 15

D. 20

Xem đáp án

Câu 102:

Cho quy tắc f: Z → R thỏa mãn f(x) = 2x + 1. Khi đó f là:

A. Hàm đơn ánh.

B. Hàm toàn ánh

C. Hàm song ánh

Xem đáp án

Câu 103:

Cho hàm số $f (x) = 3 x^{2} + 2 x + 1$ và $g (x) = 5 x - 2$ , với x $\in$ ℝ . Khi đó g.f(2) bằng:

A. 53

B. 209

C. 83

D. 25

Xem đáp án

Câu 104:

Cho hàm số $f (x) = 3 x^{2} + 2 x + 1$ và $g (x) = 5 x - 2$ , với x $\in$ ℝ . Khi đó g.f(2) bằng:

A. 53

B. 209

C. 83

D. 25

Xem đáp án

Câu 105:

Cho tập A = {-2, -1, 0, 1, 2}. Hỏi tập nào bằng tập A?

A. {a | a là số nguyên sao cho 0 < a2 < 4}

B. {a | a là số tự nhiên có |a| < 3}

C. {a | a là số thực sao cho 0 < b2 < 5}

D. {a| a là số nguyên sao cho a2 ≤ ≤ 4}

Xem đáp án

Câu 106:

Cho tập A = {a, b, c, {3, 4, 5}, (a,b), ∅ ∅ }. Lực lượng của A bằng:

A. 8

B. 5

C. 6

D. 9

Xem đáp án

Câu 107:

Cho quan hệ R = {(a,b) |a| b} trên tập số nguyên dương. Hỏi R không có tính chất nào?

A. Phản xạ

B. Đối xứng

C. Bắc cầu

D. Phản đối xứng

Xem đáp án

Câu 108:

Cho quan hệ R = {(a,b)| a ≡ b(mod 4)} trên tập {-8, -7, …,7, 8}. Hãy xác định [1]R?

A. {-8, -4, 1, 4, 8}

B. {-7, -3, 1, 5}

C. {-5, -1, 3, 7}

D. {1}

Xem đáp án

Câu 109:

Cho tập A = {-12, -11,…11, 12} và quan hệ tương đương trên A: R = {(a,b)| a ≡ b(mod 4)}. Hỏi R sẽ tạo ra một phân hoạch gồm bao nhiêu tập con trên A?

A. 0

B. 2

C. 3

D. 4

Xem đáp án

Câu 110:

Cho tập A={1, 2, 3, 4}. Trong các quan hệ trên tập A cho dưới đây, quan hệ nào thỏa mãn cả phản xạ, đối xứng, bắc cầu?

A. {(1, 1), (1, 2), (1,3), (2,2), (2,1), (2,3), (3,3)}

B. {(1, 1), (3,3), (2,3), (2,1), (3,2), (1,3)}

C. {(1, 1), (2, 2), (3,3), (4,4), (2,1), (2,3), (3,1)}

D. {(1,1), (1,2), (2,1), (2,2), (3,3), (4,4), (3,4), (4,3) }

Xem đáp án

Câu 111:

Cho tập S và một phân hoạch của S gồm 2 tập A và B. Câu nào dưới đây là sai:

A. A ∩ B = ∅ A ∩ B = ∅

B. A ∪ B = S A ∪ B = S

C. A x B = S

D. A – B = A.

Xem đáp án

Câu 112:

Cho tập A = {-12, -11,…11, 12} và quan hệ tương đương trên A: R = {(a,b)| a≡b(mod 3)}. Hỏi R sẽ tạo ra một phân hoạch gồm bao nhiêu tập con trên A?

A. 0

B. 2

C. 3

D. 4

Xem đáp án

Câu 113:

Trong số các quan hệ hai ngôi dưới đây, quan hệ nào có tính phản đối xứng?

A. R = {(a,b)| a ≤ b} trên tập số nguyên

B. {(1,1), (1,2), (2,2), (2,3), (3,2), (3,3)} trên tập {1,2,3}

C. {(a,b), (a,c), (b,b), (b,c), (c,c), (c,a)} trên tập {a,b,c}

D. R = {(a,b)| a≡b(mod 3)} trên tập {-15, -14, …, 14, 15}

Xem đáp án

Câu 114:

Cho quan hệ R = {(1,1), (1,2), (2,2), (2,3), (3,1), (3,3)} trên tập {1,2,3}. Hỏi phát biểu nào sau đây là đúng?

A. R là quan hệ tương đương

B. R là quan hệ thứ tự

C. R có tính bắc cầu

D. R không có tính bắc cầu

Xem đáp án

Câu 115:

Cho tập A = {-12, -11, …, 11, 12}, và quan hệ R = {(a,b)| a ≡ b (mod 3)}. Hãy cho biết tập nào trong số các tập sau là lớp tương đương của phần tử -8?

A. {-11, 4, -8, -5, 1, 7, 10, -2}

B. {-12, 3, -8, 5, -2, 4, -10}

C. {-1, 4, 6, -9, -8, -4, 3, 9}

D. {-9, 6, 1, -8, 3, -5, 0, -12}

Xem đáp án

Câu 116:

Cho một tập S = {0, 1, 2}, câu nào dưới đây là đúng:

A. Có 2 cách phân hoạch tập S

B. Có 3 cách phân hoạch tập S.

C. Có 4 cách phân hoạch tập S.

D. Có 5 cách phân hoạch tập S

Xem đáp án

Câu 117:

Cho tập A= {a, b, c, d}, hỏi quan hệ nào trong số các quan hệ trên A dưới đây có tính phản đối xứng?

A. R = {(a,a), (a,b), (b,c), (b,d), (c,c), (c,b), (d,a), (d,b)}

B. R = {(a,a), (a,c), (a,d), (c, b),(c,c), (d,b), (d,c)}

C. R = {(a,a), (a,b), (a,c), (b,b), (b,c), (c,c), (c,a), (d,d), (d,b)}

D. R = {(a,a), (a,c), (b,b), (b,d), (c,c), (c,a), (d,d), (d,c)}

Xem đáp án

Câu 118:

Cho quan hệ R = {(a,b)| a ≡ b(mod 5)} trên tập {-12, -11, …,11, 12}. Hãy xác định [2] _R?

A. {-9, -3, 2, 7, 12}

B. {-12, -7, -2, 2, 7, 12}

C. {-8, -3, 2, 7, 12}

D. {2}

Xem đáp án

Câu 119:

Cho tập A = { 1, 2, 3, 4, 5, 6 } và quan hệ R ⊆ A x A được xác định như sau: Với mọi a, b A, aRb khi và chỉ khi hiệu a - b là một số chẵn. Quan hệ R là:

A. R= {(1, 1), (2, 2), (3, 3),(4, 4), (5, 5), (6, 6), (1, 3), (3,1),(1, 5), (5, 1),(2, 4), (4, 2), (2,6), (6,2), (3,5), (5,3), (4,6), (6,4)}

B. R= {(1, 1), (2, 2), (3, 3),(4, 4), (5, 5), (6, 6), (3,1),(5, 1), (4, 2), (6,2), (5,3), (6,4)}

C. R= {(1, 3), (3,1),(1, 5), (5, 1),(2, 4), (4, 2), (2,6), (6,2), (3,5), (5,3), (4,6), (6,4)}

D. R= {( (3,1), (5, 1), (4, 2), (6,2), (5,3), (6,4)}

Xem đáp án

Câu 120:

Cho tập A = { 1, 2, 3, 4, 5, 6 } và quan hệ R ⊆ A x A với:

R= {(1,1), (2,2), (3,3),(4,4), (5,5), (6,6), (1,3), (3,1),(1, 5), (5, 1),(2, 4), (4, 2), (2,6), (6,2), (3,5), (5,3), (4,6), (6,4)}

Ma trận biểu diễn R là:

A.

[\begin{matrix} 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \end{matrix}]

B.

[\begin{matrix} 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 & 1 \end{matrix}]

C.

[\begin{matrix} 1 & 0 & 1 & 1 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \end{matrix}]

D.

[\begin{matrix} 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 & 0 \end{matrix}]

Xem đáp án

Câu 121:

Nhận xét nào sau đây là SAI:

A. Một quan hệ có tính phản xạ khi và chỉ khi ma trận biểu diễn nó có tất cả các phần tử trên đường chéo chính đều bằng 1

B. Một quan hệ có tính đối xứng khi và chỉ khi ma trận biểu diễn nó là một ma trận đối xứng qua đường chéo chính

C. Một quan hệ có tính phản xạ khi và chỉ khi đồ thị biểu diễn nó tại mỗi đỉnh đều có khuyên

D. Một quan hệ có tính bắc cầu khi và chỉ khi đồ thị biểu diễn nó có cung đi từ đỉnh a đến đỉnh b thì cũng có cung đi từ đỉnh b đến đỉnh c

Xem đáp án

Câu 122:

Cho A là một tập hữu hạn khác rỗng. Quan hệ R⊆ AxA. Phát biểu nào sau đây là ĐÚNG:

A. Quan hệ R có tính phản xạ nếu mọi phần tử a thuộc A đều có quan hệ R với chính nó.

B. Quan hệ R có tính đối xứng nếu mọi a, b thuộc A thì a phải có quan hệ R với b.

C. Quan hệ R có tính bắc cầu nếu mọi a, b, c thuộc A thì a phải có quan hệ R với b và b phải có quan hệ R với c

Xem đáp án

Câu 123:

Cho biết quan hệ nào là quan hệ tương đương trên tập {a, b, c, d}:

A. {(a, a), (b, b), (c, c), (d, d), (a, b), (a, c), (a, d)}

B. {(a, a), (b, b), (c, c), (d, d), (a, b), (b, a)}

C. {(a, a), (a, c), (c, a), (c, c), (c, d), (d, c), (d, d)}

D. {(a, a), (b, b), (c, c), (d, d) , (c, d), (d, c), (d, a), (b, d)}

Xem đáp án

Câu 124:

Cho A ={11, 12, 13, 14, 15}. Quan hệ R được xác định: ∀ a , b ∈ A , a R b ⇔ a + b = 2 k ( k = 1 , 2 , . . . ) ∀ a , b ∈ A , a R b ⇔ a + b = 2 k ( k = 1 , 2 , . . . ) . Quan hệ R được biểu diễn là:

A. {(11, 11), (12, 12), (13, 13), (14, 14), (11, 13), (13, 11), (11, 15), (15, 11), (12, 14), (14, 12)}

B. {(11, 11), (12, 12), (13, 13), (14, 14), (15, 15), (11, 13), (11, 15), (13, 15), (12, 14)}

C. {(11, 13), (13, 11), (11, 15), (15, 11), (13, 15), (15, 13), (12, 14), (14, 12)}

D. {(11,11), (12, 12), (13, 13), (14, 14), (15, 15), (11,13), (13, 11), (11, 15), (15, 11), (13, 15), (15, 13), (12, 14), (14, 12)}

Xem đáp án

Câu 125:

Cho A = {11, 12, 13, 14, 15}. Trên A xác định quan hệ R như sau: ∀ a , b ∈ A , a R b ⇔ a + b = 2 k + 1 ( k = 1 , 2 , . . . ) ∀ a , b ∈ A , a R b ⇔ a + b = 2 k + 1 ( k = 1 , 2 , . . . ) . Quan hệ R được biểu diễn là:

A. {(11, 12), (11, 14), (12, 13), (12, 15)}

B. {(11, 11), (12, 12), (13, 13), (14,14), (15,15), (11, 12), (11, 14), (12, 13), (12, 15)}

C. {(11, 12), (12, 11), (11, 14), (14, 11), (12, 15), (15, 12)}

D. {(11, 12), (12, 11), (11, 14), (14, 11), (12, 15), (15, 12), (13, 14), (14, 13), (12, 13), (13, 12), (14, 15), (15, 14)}

Xem đáp án

Câu 126:

Cho tập A = {1, 2, 3, 4, 5, 6}. Cho A₁ = {1}, A₂ = {2}, A₃ = {3, 4}, A₄ = {5, 6}. Quan hệ tương đương R trên A sinh ra phân hoạch A₁, A₂, A₃, A₄ là:

A. {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (3, 4), (4, 3), (5, 6), (6, 5)}

B. {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (1, 2), (2, 1), (3, 4), (4, 3)}

C. {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (2, 3), (3, 2), (4, 5), (5, 4)}

D. {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (4, 5), (5, 4), (1, 2), (2, 1), (1, 3), (3, 1)}

Xem đáp án

Câu 127:

Cho tập A = {1, 2, 3, 4, 5, 6}. Cho A₁ = {1, 2, 3}, A₂ = {4, 5}, A₃ = {6}. Quan hệ tương đương R trên A sinh ra phân hoạch A₁, A₂, A₃ là:

A. {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (1,2), (2,1), (1,3), (3,1), (2,3), (3,2), (4,5), (5,4)}

B. {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (1,2), (2,1), (1,3),(3, 1),(5, 6), (6,5)}

C. {(1,1), (1,2), (2,2), (3,4), (3,3), (5,6), (4,4), (5,5), (6,6)}

D. {(1,1), (2,2), (3,3), (4,4), (5,5), (6, 6), (1,2), (2,1), (1,3), (3,1), (3,4), (4,3)}

Xem đáp án

Câu 128:

Cho tập A = {1, 2, 3, 4, 5, 6} và quan hệ tương đương R trên A như sau: R = {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (1,2), (2,1), (4,5), (5,4)}. Xác định phân hoạch do R sinh ra:

A. A1 = {1, 2, 3}, A2 = {4, 5, 6}

B. A1 = {1, 2}, A2 = {3}, A3 = {4,5}, A4 = {6}

C. A1 = {1}, A2 = {2,4}, A3 = {3}, A4 = {5, 6}

D. A1 = {1,2}, A2 = {3, 4}, A3 = {5, 6}

Xem đáp án

Câu 129:

Cho A = {1, 2, 3, 4, 5, 6}. Quan hệ R được xác định: ∀ a , b ∈ A , a R b ⇔ a + b = 2 k ( k = 1 , 2 , . . . ) ∀ a , b ∈ A , a R b ⇔ a + b = 2 k ( k = 1 , 2 , . . . ) . Xác định phân hoạch do R sinh ra:

A. A1 = {1,3}, A2 = {2,4}, A3 = {5}

B. A1 = {1}, A2 = {2,4}, A3 = {3}, A4 = {5}

C. A1 = {1}, A2 = {2}, A3 = {3}, A4 = {4},A5 = {5}

D. A1 = {1,3,5}, A2 = {2,4}

Xem đáp án

Câu 130:

Hãy liệt kê quan hệ R trên tập hợp {1,2,3,4,5} biết ma trận biểu diễn như sau:

$[\begin{matrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 \end{matrix}]$

A. {(1,1),(2,2),(3,3),(4,4),(5,5),(2,3),(3,2),(2,4),(4,2),(4,5),(5,4)}

B. {(1,1),(2,2),(3,3),(4,4),(5,5),(2,3),(3,2),(3,4),(4,3),(4,5),(5,4)}

C. {(1,1),(2,2),(3,3),(4,4),(5,5),(2,3),(3,2),(3,5),(5,3),(4,5),(5,4)}

D. {(1,1),(2,2),(3,3),(4,4),(5,5),(2,4),(4,2),(3,4),(4,3),(4,5),(5,4)}

Xem đáp án

Câu 131:

Cho quan hệ R = {(a,b) | a b (mod n) } trên tập số nguyên dương. Hỏi R KHÔNG có tính chất nào?

A. Phản xạ

B. Đối xứng

C. Bắc cầu

D. Phản đối xứng

Xem đáp án

Câu 132:

Cho tập A = {1, 2, 3, 4, 5}.Trong các quan hệ trên tập A cho dưới đây, quan hệ nào là quan hệ tương đương?

A. {(1,1), (1,2), (1,3), (2,2), (2,1), (2,3), (3,3), (1,5), (5,1)}

B. {(1,1), (2,2), (3,3), (4,4), (5,5), (1,2), (2,1), (1,3), (3,1)}

C. {(1,1), (1,2), (2,1), (2,2), (3,3), (4,4)}

D. {(1,1), (2,2), (3,3), (4,4), (5,5), (2,1), (1,2), (3,4), (4,3)}

Xem đáp án

Câu 133:

Cho quan hệ R = {(a,b)| a ≡ b(mod 4)} trên tập {-10, -9, …,9, 10}. Hãy xác định [2]_R?

A. {-10, -6, -2, 2, 6, 10}

B. {2, 4, 6, 8, 10}

C. {-10, -8, -6, -4,-2}

D. {-8, -6, -4, -2, 2, 4, 6, 8}

Xem đáp án

Câu 134:

Cho tập A = {-12, -11, …, 11, 12}, và quan hệ R = {(a,b)| a ≡ b (mod 4)}. Hãy cho biết tập nào trong số các tập sau là lớp tương đương của phần tử -7?

A. {-9, -5, -1, 3, 7, 10}

B. {-11, -7, -3, 1, 5, 9}

C. {-11, -3, 1, , 3, 9}

D. {-9, 6, 1, -8, 3, -5, 0, -12}

Xem đáp án

Câu 135:

Cho một tập S = {1, 2, 3, 4}, câu nào dưới đây là đúng:

A. Có 10 cách phân hoạch tập S.

B. Có 11 cách phân hoạch tập S.

C. Có 12 cách phân hoạch tập S

D. Có 13 cách phân hoạch tập S

Xem đáp án

Câu 136:

Cho tập A= {5, 6, 7, 8}, hỏi quan hệ nào trong số các quan hệ trên A dưới đây có tính phản đối xứng?

A. R = {(5,5), (5,7), (5,8), (7,6), (7,7), (8,6), (8,7)}

B. R = {(5,5), (5,6), (6,7), (7,6) ,(6,8), (7,7), (8,5), (8,6)}

C. R = {(5,5), (5,6), (5,7), (7,5),(6,6), (6,7), (7,7), (8,8), (8,6)}

D. R = {(5,5), (5,7), (7,5), (6,6), (6,8), (7,7), (8,8), (8,7)}

Xem đáp án

Câu 137:

Cho quan hệ R = {(a,b)| a ≡ b(mod 6)} trên tập {-15, -11, …,11, 15}. Hãy xác định [5]R?

A. {-13, -7, -1, 5, 11}

B. {-10, -4, 2, 5, 8, 14}

C. {-15, -9, -3, 3, 5, 9, 15}

D. {-14, -8, -2, 4, 5, 10}

Xem đáp án

Câu 138:

Cho tập A = { 1, 2, 3, 4, 5, 6 } và quan hệ R ⊆ A x A được xác định như sau: Với mọi a, b ∈ ∈ A, aRb khi và chỉ khi hiệu 2a-b = 0. Quan hệ R là:

A. R= {(1, 2), (2, 4), (3, 6)}

B. R= {(1, 1), (2, 2), (3, 3),(4, 4), (5, 5), (6, 6)}

C. R= {(1, 2), (2,1),(2, 4), (4, 2), (3, 6), (6, 3)}

D. R= {(1,1), (2, 2), (3,3), (4,4), (5,5), (6,6), (2,4), (4,6)}

Xem đáp án

Câu 139:

Giả sử P và Q là 2 mệnh đề. Tuyển của 2 mệnh đề (P v Q) là một mệnh đề… ?

A. Chỉ đúng khi cả P và Q cùng đúng

B. Chỉ sai khi cả P và Q cùng sai

C. Chỉ đúng khi P đúng Q sai

D. Chỉ sai khi P đúng Q sai

Xem đáp án

Câu 140:

Hãy cho biết khẳng định nào sau đây không phải là 1 mệnh đề?

A. 2 + 3 < 4

B. 3 là 1 số chẵn

C. Cho x là một số nguyên dương

D. 1 - 2 < 0

Xem đáp án

Câu 141:

Giả sử P và Q là 2 mệnh đề. Hội của 2 mệnh đề (P ^ Q) là một mệnh đề…?

A. Nhận chân trị đúng khi cả P và Q cùng đúng. Chỉ sai khi 1 trong 2 mệnh đề P, Q nhận chân trị sai

B. Nhận chân trị đúng khi ít nhất 1 trong 2 mệnh đề P và Q đúng. Chỉ sai cả 2 mệnh đề P, Q nhận chân trị sai.

C. Chỉ nhận chân trị đúng khi P đúng Q sai hoặc Q đúng P sai.

D. Nhận chân trị sai khi 1 trong 2 mệnh đề hoặc cả 2 mệnh đề P và Q sai. Chỉ đúng khi và chỉ khi cả 2 mệnh đề P, Q nhận chân trị đúng.

Xem đáp án

Câu 142:

Giả sử P và Q là 2 mệnh đề, P→Q là một mệnh đề…?

A. Chỉ nhận chân trị sai khi P đúng Q sai. Nhận chân trị đúng trong các trường hợp còn lại.

B. Chỉ nhận chân trị sai khi P sai Q đúng. Nhận chân trị đúng trong các trường hợp còn lại.

C. Chỉ nhận chân trị đúng khi P sai Q đúng. Nhận chân trị sai trong các trường hợp còn lại.

D. Nhận chân trị đúng khi 1 trong 2 mệnh đề nhận chân trị đúng, sai trong các trường hợp còn lại.

Xem đáp án

Câu 143:

Giả sử P và Q là 2 mệnh đề, chọn đáp án đúng cho định nghĩa mệnh đề P→Q?

A. Là một mệnh đề nhận chân trị đúng khi một trong hai hoặc cả 2 mệnh đề cùng đúng, nhận chân trị sai trong các trường hợp còn lại.

B. Là một mệnh đề nhận chân trị đúng khi P và Q có cùng chân trị. Nhận chân trị sai trong các trường hợp còn lại.

C. Là một mệnh đề nhận chân trị đúng khi P sai hoặc cả P và Q cùng đúng. Nhận chân trị sai khi và chỉ khi P đúng Q sai

D. Là 1 mệnh đề nhận chân trị đúng khi P và Q cùng đúng, sai khi P và Q cùng sai.

Xem đáp án

Câu 144:

Giả sử P và Q là 2 mệnh đề, chọn đáp án đúng cho định nghĩa mệnh đề P ↔ ↔ Q?

A. Là mệnh đề có chân trị đúng khi P và Q có cùng chân trị, sai trong các trường hợp còn lại

B. Là 1 mệnh đề nhận chân trị đúng khi P và Q cùng đúng, sai khi P và Q cùng sai.

C. Là một mệnh đề nhận chân trị đúng khi một trong hai hoặc cả 2 mệnh đề cùng đúng, nhận chân trị sai trong các trường hợp còn lại.

D. Là một mệnh đề nhận chân trị đúng khi P sai hoặc cả P và Q cùng đúng. Nhận chân trị sai khi và chỉ khi P đúng Q sai

Xem đáp án

Câu 145:

Biểu thức hằng đúng là?

A. Biểu thức chỉ nhận chân trị đúng khi các biến mệnh đề nhận chân trị đúng.

B. Biểu thức nhận chân trị đúng trong mọi trường hợp về chân trị của bộ biến mệnh đề

C. Biểu thức nhận chân trị sai trong mọi trường hợp về chân trị của bộ biến mệnh đề

D. Biểu thức chỉ nhận chân trị sai khi các biến mệnh đề nhận chân trị sai.

Xem đáp án

Câu 146:

Biểu thức hằng sai là?

A. Biểu thức chỉ nhận chân trị đúng khi các biến mệnh đề nhận chân trị đúng

B. Biểu thức nhận chân trị đúng trong mọi trường hợp về chân trị của bộ biến mệnh đề.

C. Biểu thức nhận chân trị sai trong mọi trường hợp về chân trị của bộ biến mệnh đề

D. Biểu thức chỉ nhận chân trị sai khi các biến mệnh đề nhận chân trị sai

Xem đáp án

Câu 147:

Hai biểu thức mệnh đề E, F (có cùng bộ biến mệnh đề) được gọi là tương đương logic nếu…?

A. Nếu E có chân trị đúng thì F có chân trị sai và ngược lại.

B. E và F cùng có chân trị đúng.

C. E và F cùng có chân trị sai.

D. E và F có cùng chân trị trong mọi trường hợp về chân trị của bộ biến mệnh đề.

Xem đáp án

Câu 148:

Cho A = {2, 3, 6}. Hãy cho biết tập A có tối đa bao nhiêu tập con?

A. 3

B. 4

C. 5

D. 8

Xem đáp án

Câu 149:

Cho A = {1,3,3,3,5,5,5,5,5} và B = {1,3,5}. Đáp án nào dưới đây mô tả chính xác nhất mối quan hệ giữa A và B:

A. Khác nhau

B. A là con B

C. Bằng nhau

D. B là con A

Xem đáp án

Câu 150:

Cho các đẳng thức sau, có thể kết luận gì về các tập hợp A và B? A+ B = A, A + B = A

A. Bằng nhau B.

A là con B

C. Rời nhau

D. B là con A

Xem đáp án

Câu 151:

Cho tập A = {2, 3, 4, 5}. Tập nào trong các tập dưới đây không bằng A?

A. {4, 3, 5, 2}

B. {a | a là số tự nhiên lớn hơn 1 và nhỏ hơn 6}

C. {b | b là số thực sao cho 1 < b2 < 36}

D. {2, 2, 3, 4, 4, 4, 5}

Xem đáp án

Câu 152:

Cho biết quan hệ “lớn hơn hoặc bằng” trên tập Z có những tính chất nào?

A. Phạn xạ - đối xứng

B. Phản xạ - đối xứng – bắc cầu

C. Phản xạ - đối xứng – phản đối xứng

D. Phản xạ - phản đối xứng – bắc cầu

Xem đáp án

Câu 153:

Hãy cho biết quan hệ “cùng quê” của 2 sinh viên có bao nhiêu tính chất?

A. Đối xứng

B. Đối xứng – bắc cầu

C. Phản xạ - đối xứng – bắc cầu

D. Phản xạ - phản đối xứng – bắc cầu

Xem đáp án

Câu 154:

Hãy cho biết khẳng định nào dưới đây không phải là một mệnh đề?

A. 2 + 2 < 3

B. 3 * 2 = 6

C. x + 1 = 2

D. 3 - 1 > 2

Xem đáp án

Câu 155:

Biểu thức logic không chứa thành phần nào dưới đây:

A. Các mệnh đề

B. Các vị từ

C. Các biến mệnh đề

D. Các phép toán logic

Xem đáp án

Câu 156:

Để chứng minh một quy tắc suy luận đúng ta thường sử dụng các phương pháp:

A. Định nghĩa, biến đổi tương đương logic

B. Lập bảng giá trị chân lý và kết luận theo định nghĩa

C. Biến đổi tương đương logic

D. Chứng minh trực tiếp

Xem đáp án

Câu 157:

Đoạn dưới đây chứng minh “3n + 2 là lẻ thì n là lẻ”: Vì 3n + 2 lẻ là đúng ta có 2 là số chẵn nên 3n là số lẻ, mà 3 là số lẻ nên n là số lẻ. Vậy ta đã có thể kết luận n là lẻ. Đoạn trên sử dụng phương pháp chứng minh nào:

A. Gián tiếp

B. Trực tiếp

C. Phân chia trường hợp

D. Phản chứng

Xem đáp án

Câu 158:

Để chứng minh tích của 3 số tự nhiên liên tiếp luôn chia hết cho 6, người ta chứng minh như sau:

- Đặt P(n) = n(n+1)(n+2). P(n) chia hết cho 6 với n>0.

- Ta có, với n = 1; P(1) = 1.2.3 = 6, chia hết cho 6

- Giả sử P(n) đúng , ta đi chứng minh (n+1) (n+2)(n+3) chia hết cho 6.

- Ta có, (n+1) (n+2)(n+3) = n(n+1)(n+2) + 3(n+1)(n+2).

- Ta đã có n(n+1)(n+2) chia hết cho 6. Mặt khác (n+1)(n+2) luôn chia hết cho 2 (kết quả này đã được chứng minh). Do vậy, 3(n+1)(n+2) chia hết cho 6. Như vậy ta được điều phải chứng minh.

Đoạn trên sử dụng phương pháp nào?

A. Chứng minh qui nạp mạnh

B. Chứng minh trực tiếp

C. Chứng minh quy nạp yếu

D. Chứng minh phản chứng.

Xem đáp án

Câu 159:

Tập hợp là:

A. Một nhóm các đối tượng hay vật thể có chung tính chất nào đó.

B. Một nhóm các đối tượng và vật thể có chung tính chất nào đó.

C. Một nhóm các đối tượng và vật thể có chung duy nhất một tính chất nào đó.

D. Một nhóm các phần tử có chung duy nhất một tính chất nào đó

Xem đáp án

Câu 160:

Cho A và B là hai tập hợp. Phép hợp của A và B được ký hiệu A + B, là:

A. Tập chứa tất cả các phần tử thuộc A và đồng thời thuộc B.

B. Tập chứa tất cả các phần tử hoặc thuộc tập hợp A hoặc thuộc tập hợp B

C. Tập bao gồm những phần tử không thuộc A.

D. Tập chứa các phần tử thuộc tập hợp A nhưng không thuộc tập hợp B.

Xem đáp án

Câu 161:

Cho A và B là hai tập hợp. Phép giao của A và B được ký hiệu A + B, là:

A. Tập bao gồm những phần tử không thuộc A

B. Tập chứa các phần tử thuộc tập hợp A nhưng không thuộc tập hợp B.

C. Tập chứa tất cả các phần tử thuộc A và đồng thời thuộc B.

D. Tập chứa tất cả các phần tử hoặc thuộc tập hợp A hoặc thuộc tập hợp B.

Xem đáp án

Câu 162:

Cho A và B là hai tập hợp. Hiệu của A và B được ký hiệu A-B, là:

A. Tập chứa tất cả các phần tử thuộc A và đồng thời thuộc B.

B. Tập chứa tất cả các phần tử hoặc thuộc tập hợp A hoặc thuộc tập hợp B.

C. Tập chứa các phần tử thuộc tập hợp A nhưng không thuộc tập hợp B.

D. Tập bao gồm những phần tử không thuộc A.

Xem đáp án

Câu 163:

Cho A và B là hai tập hợp. Hiệu đối xứng của A và B được ký hiệu A - B, là:

A. Tập chứa tất cả các phần tử chỉ thuộc A hoặc chỉ thuộc B, đồng thời thuộc cả A và B.

B. Tập chứa tất cả các phần tử chỉ thuộc A hoặc chỉ thuộc B, không đồng thời thuộc cả A và B.

C. Tập chứa tất cả các phần tử chỉ thuộc A và thuộc B, không đồng thời thuộc cả A và B.

D. Tập chứa tất cả các phần tử chỉ thuộc A và thuộc B, đồng thời thuộc cả A hoặc B.

Xem đáp án

Câu 164:

Cho A, B là 2 tập hợp. A là tập con của B được ký hiệu A x B, khi:

A. Tồn tại phần tử thuộc A thì tồn tại phần tử thuộc B

B. Tồn tại phần tử thuộc A thì cũng thuộc B

C. Mọi phần tử thuộc A thì tồn tại phần tử thuộc B

D. Mọi phần tử thuộc A đều thuộc B

Xem đáp án

Câu 165:

Cho A là tập hữu hạn, B là tập vũ trụ. Phần bù của A trong B là:

A. Tập chứa tất cả các phần tử hoặc thuộc tập hợp A hoặc thuộc tập hợp B.

B. Tập chứa các phần tử thuộc tập hợp A nhưng không thuộc tập hợp B.

C. Tập bao gồm những phần tử thuộc tập A và tập B.

D. Tập bao gồm những phần tử không thuộc A nhưng lại thuộc B

Xem đáp án

Câu 166:

Cho A = {2, 3, 5}, B = {3, 2, 5}. Hãy cho biết A và B có quan hệ như thế nào với nhau:

A. Khác nhau

B. B là con của A

C. Bằng nhau

D. A là con của B

Xem đáp án

Câu 167:

Quan hệ tương đương là một quan hệ 2 ngôi và có các tính chất:

A. Phản xạ, phản đối xứng, đối xứng

B. Phản xạ, đối xứng, bắc cầu

C. Phản xạ, phản đối xứng, bắc cầu

D. Phản xạ, đối xứng, phản đối xứng, bắc cầu

Xem đáp án

Câu 168:

Quan hệ thứ tự là một quan hệ 2 ngôi và có các tính chất:

A. Phản xạ, phản đối xứng, đối xứng

B. Phản xạ, đối xứng, bắc cầu

C. Phản xạ, phản đối xứng, bắc cầu

D. Phản xạ, đối xứng, phản đối xứng, bắc cầu

Xem đáp án

Câu 169:

Đáp án nào dưới đây là khái niệm mệnh đề?

A. Mệnh đề là một khẳng định luôn đúng

B. Mệnh đề là một khẳng định vừa đúng vừa sai

C. Mệnh đề là một khẳng định hoặc đúng hoặc sai, không thể vừa đúng vừa sai

D. Mệnh đề là một khẳng định luôn sai

Xem đáp án

Câu 170:

Giả sử p và q là các mệnh đề. Hãy cho biết định nghĩa đúng của mệnh đề p*q.

A. Là một mệnh đề mà chỉ nhận giá trị T khi và chỉ khi p, q nhận giá trị T. Nhận giá trị F trong các trường hợp còn lại.

B. Là một mệnh đề chỉ đúng khi một trong p hoặc q là đúng và sai trong các trường hợp khác còn lại.

C. Là một mệnh đề mà nó chỉ nhận giá trị T khi và chỉ khi ít nhất một trong hai mệnh đề p, q nhận giá trị T. Nhận giá trị F khi và chỉ khi cả p, q đều nhận giá trị F.

D. Là một mệnh đề nhận giá T khi và chỉ khi p nhận giá trị F hoặc p và q cùng nhận giá trị T. Nhận giá trị F khi và chỉ khi p nhận giá trị T và q nhận giá trị F.

Xem đáp án

Câu 171:

Giả sử p và q là các mệnh đề. Hãy cho biết định nghĩa đúng của mệnh đề p XOR q.

A. Là một mệnh đề chỉ đúng khi một trong p hoặc q là đúng và sai trong các trường hợp khác còn lại.

B. Là một mệnh đề nhận giá T khi và chỉ khi p nhận giá trị F hoặc p và q cùng nhận giá trị T. Nhận giá trị F khi và chỉ khi p nhận giá trị T và q nhận giá trị F.

C. Là một mệnh đề mà nó chỉ nhận giá trị T khi và chỉ khi ít nhất một trong hai mệnh đề p, q nhận giá trị T. Nhận giá trị F khi và chỉ khi cả p, q đều nhận giá trị F.

D. Là một mệnh đề mà nó chỉ nhận giá trị T khi và chỉ khi p, q nhận giá trị T. Nhận giá trị F khi và chỉ khi hoặc p, q, hoặc cả hai nhận giá trị F

Xem đáp án

Câu 172:

Biểu thức logic A được gọi là hằng đúng nếu:

A. A nhận giá trị True khi tồn tại giá trị chân lý của bộ biến mệnh đề có mặt trong A.

B. A nhận giá trị True với giá trị chân lý của bộ biến mệnh đề có mặt trong A.

C. A nhận giá trị True với mọi hệ giá trị chân lý của bộ biến mệnh đề có mặt trong A

D. A nhận giá trị False với mọi hệ giá trị chân lý của bộ biến mệnh đề có mặt trong A.

Xem đáp án

Câu 173:

Biểu thức logic A được gọi là hằng sai nếu:

A. A nhận giá trị với mọi hệ giá trị chân lý của bộ biến mệnh đề có mặt trong A.

B. A nhận giá trị False với mọi hệ giá trị chân lý của bộ biến mệnh đề có mặt trong

A. C. A nhận giá trị True với mọi hệ giá trị chân lý của bộ biến mệnh đề có mặt trong A.

D. A nhận giá trị False khi tồn tại hệ giá trị chân lý của bộ biến mệnh đề có mặt trong A.

Xem đáp án

Câu 174:

Có thể đưa một bài toán chứng minh về loại mệnh đề nào?

A. Hội

B. Tuyển

C. Kéo theo

D. Tương đương

Xem đáp án

Câu 175:

Phương pháp chứng minh đi từ giả thiết đến kết luận thông qua các luật suy diễn, các định lý, các nguyên lý hay các kết quả đã có từ trước được gọi là phương pháp chứng minh:

A. Gián tiếp

B. Trực tiếp

C. Tầm thường

D. Theo giả thiết

Xem đáp án

Câu 176:

Thứ tự thực hiện các phép toán trong đại số Boole là:

A. ( ) – Bù – tổng – tích.

B. ( ) – Bù – tích – tổng.

C. Bù – tổng – tích – ( ).

D. Bù – tích – tổng – ( ).

Xem đáp án

Câu 177:

Hai biểu thức boole gọi là tương đương nhau nếu chúng:

A. Có cùng giá trị chân lý trong mọi trường hợp giá trị của các biến Boole.

B. Có cùng số biến và có cùng giá trị chân lý.

C. Cùng biểu diễn một hàm boole, số biến bằng nhau.

D. Có số biến bằng nhau và biểu diễn 2 hàm boole giống hoặc khác nhau.

Xem đáp án

Câu 178:

Cho A = {a, b, c, 0, 1}; B ={0, a, 1, a, 2, 3}. Hãy cho biết A + B là tập nào?

A. {0, 1}

B. { a, 0, 1}

C. { a, 0, 1, 2, 3}

D. { 0, 1, 2}

Xem đáp án

Câu 179:

Cho A = { 2, 0, 3, 1, 3}; B ={4, 2, 3}. Hãy cho biết A + B là tập nào?

A. {2, 3}

B. { 2, 0, 3, 1}

C. { 2, 0, 1, 4, 3}

D. { 2, 0, 3, 4}

Xem đáp án

Câu 180:

Cho A = {0, 1}, B = {a, b, c}. Tập AxB là:

A. {(a, b), (b, 0) (a,1), (b,1), (c,0), (1, c) }

B. { (0, a), (0, b), (1, a), (1,b ), (0, c), (1,c)}

C. { (1, a), (0, 1), (0, b), (0, c), (1, b), (1, c) }

D. { (0, a), (0, b), (0, c), (a, 1), (b, 1), (c, 1) }

Xem đáp án

Câu 181:

Cho A = {1, 2, 4}, B = {2, 4, 5, 7}. Tập (A+B) + A là:

A. {1, 2, 4, 5, 7}

B. {1, 5, 7}

C. {2, 4}

D. {1, 2, 4}

Xem đáp án

Câu 182:

Cho A = {c, d, g}, B = {a, c, g, k}. Tập (A+B) + (A+B) là

A. {c, d, g}

B. {c, d, g, a, k}

C. {a, d, k}

D. {c, g}

Xem đáp án

Câu 183:

Cho A = {1, 2, 3, 4}, B = {2, 4, 6, 8}, C = {1, 3, 5, 7}. Tập ((A+B) +C) + ((A+C) +B) là:

A. {1, 2, 3, 4, 5, 7}

B. {2, 4}

C. {1, 2, 3, 4, 6, 8}

D. {1, 2, 3, 4, 5, 6, 7, 8}

Xem đáp án

Câu 184:

Cho A = {1, 2, 3, 4}, B = {2, 4, 6, 8}, C = {1, 3, 5, 7}. Tập ((A+C) +B) + ((B+C)\A) là:

A. {2, 4}

B. {1, 3, 5, 7}

C. {2, 4, 5, 6, 7, 8}

D. {1, 2, 3, 4, 5, 6, 7, 8}

Xem đáp án

Câu 185:

Cho A = {1, 2, 3, 5}, B = {2, 4, 6, 8}, C = {1, 6, 7}. Tập (A\B) +C là:

A. {2, 4, 6}

B. {3, 5, 7}

C. {1}

D. {1, 2, 3}

Xem đáp án

Câu 186:

Cho A = {a, b, d, h, k} ; B = {c, d, e, h}, C = {a, e, g, k). Tập (A\B) +C là:

A. {a, b, e, g, k}

B. {a, b, c, d, e}

C. {c, d, e}

D. {a, b, c, e}

Xem đáp án

Câu 187:

Cho A = {a, b, c, e} ; B = {c, d, f, g}. Tập A - B là:

A. {a, b, e}

B. {d, f, g}

C. {a, b, e, d, g, f}

D. {a, b, c, d, e, g, f}

Xem đáp án

Câu 188:

Cho A = {a, b, c, e}; B = {c, d, f, g}. Tập (A \B) +A là:

A. {a, b, g}

B. {b, c, e}

C. {a, b, c, d}

D. {a, b, c, e}

Xem đáp án

Câu 189:

Cho tập A = {1,2,a}. Tập lũy thừa của A là:

A. {{1,2,a}}

B. {+,{1},{2},{a}}

C. {+,{1},{2},{a},{1,2},{1,a},{2,a},{1,2,a}}

D. {{1},{2},{a},{1,2},{1,a},{2,a},{1,2,a}}

Xem đáp án

Câu 190:

Cho biết quan hệ nào dưới đây là quan hệ tương đương:

A. Quan hệ lớn hơn trên tập Z

B. Quan hệ đồng dư theo modulo 3 trên tập Z

C. Quan hệ chia hết trên tập Z

D. Quan hệ nhỏ hơn trên tập Z

Xem đáp án

Câu 191:

Cho tập A={1, 2, 3, 4}.Trong các quan hệ trên tập A cho dưới đây, quan hệ nào là quan hệ tương đương?

A. {(1, 1), (1, 2), (1,3), (2,2), (2,1), (2,3), (3,3)}

B. {(1, 1), (3,3), (2,3), (2,1), (3,2), (1,3)}

C. {(1,1), (1,2), (2,1), (2,2), (3,3), (4,4)}

D. {(1, 1), (2, 2), (3,3), (4,4), (2,1), (2,3), (3,1)}

Xem đáp án

Câu 192:

Trong một phiên tòa có 3 bị can, lời khai của 3 bị can đều đúng sự thật và lời khai cụ thể như sau:

- Anh An: Chị Bình có tội và anh Công vô tội

- Chị Bình: Nếu anh An có tội thì anh Công có tội

- Anh Công: Tôi vô tội nhưng một trong 2 người kia có tội.

Áp dụng logic mệnh đề cho biết ai là người có tội trong phiên tòa này:

A. Anh An

B. Chị Bình

C. Anh Công

D. Không ai có tội

Xem đáp án

Câu 193:

Cho các mệnh đề được phát biểu như sau:

- Quang là người khôn khéo - Quang không gặp may mắn

- Quang gặp may mắn nhưng không không khéo

- Nếu Quang là người khôn khéo thì không gặp may mắn

- Quang là người khôn khéo khi và chi khi Quang gặp may mắn

- Hoặc Quang là người khôn khéo, hoặc gặp may mắn nhưng không đồng thời cả hai.

Hãy cho biết có tối đa bao nhiêu mệnh đề đồng thời đúng trong số các mệnh đề trên?

A. 2

B. 3

C. 4

D. 5

Xem đáp án

Câu 194:

Cho một đoạn giả mã như sau:

Repeat

………………

Until ((x<>0) and (y>0) or (not ((w>0) and (t=3));

Hãy cho biết với bộ giá trị nào dưới đây thì vòng lặp dừng?

A. x = 7, y = 2, w = 5, t = 3

B. x = 0, y = 2, w = -3, t = 3

C. x = 0, y = -1, w = 1, t = 3

D. x = 1, y = -1, w = 1, t = 3

Xem đáp án

Câu 195:

Để chứng minh “tích của 2 số hữu tỷ là một số hữu tỷ”, ta sử dụng phương pháp nào?

A. Chứng minh gián tiếp

B. Chứng minh trực tiếp

C. Chứng minh phản chứng

D. Chứng minh phân chia trường hợp

Xem đáp án

Câu 196:

Để chứng minh “một số nguyên dương n là lẻ khi và chỉ khi 5n+6 là lẻ”, ta dùng phương pháp chứng minh nào?

A. Trực tiếp

B. Gián tiếp

C. Phản chứng

D. Quy nạp

Xem đáp án

Câu 197:

Cho hàm Boole: f ( a , b , c , d ) = a . b + b . d + d . c f ( a , b , c , d ) = a . b + b . d + d . c . Dạng tối thiểu của hàm f là:

A. f= a.b + d

B. f = (a+b).d

C. f = a.b + d

D. f = b.c +d

Xem đáp án

Câu 198:

Một giải thuật đệ qui được thực hiện thông qua hai bước:

A. Bước phân tích và bước thay thế ngược lại

B. Bước tính toán và phân tích

C. Bước thay thế ngược lại và phân tích

D. Bước phân tích và bước tính toán

Xem đáp án

Câu 199:

Khi thiết kế thuật toán đệ quy thì ta cần xác định các yêu cầu sau:

A. Xác định được phần cơ sở và phần đệ quy

B. Xác định được phần cơ sở và phần truy hồi

C. Xác định được phần suy biến và phần quy nạp

D. Xác định được phần dừng và phần lặp vô hạn

Xem đáp án

Câu 200:

Cho biết số phần tử của A1 + A2 + A3 nếu mỗi tập có 100 phần tử và các tập hợp là đôi một rời nhau?

A. 200

B. 300

C. 100

D. 0

Xem đáp án

Câu 201:

Cho biết số phần tử của A1 + A2 + A3 nếu mỗi tập có 100 phần tử và nếu có 50 phần tử chung của mỗi cặp 2 tập và có 10 phần tử chung của cả 3 tập?

A. 250

B. 160

C. 200

D. 300

Xem đáp án

Câu 202:

Giả sử trong một nhóm 6 người mỗi cặp hai người hoặc là bạn, hoặc là thù của nhau. Khi đó:

A. Trong nhóm không tồn tại ba người là bạn của nhau hoặc là kẻ thù của nhau.

B. Trong nhóm có ba người là bạn của nhau hoặc là kẻ thù của nhau.

C. Có ba người là thù của nhau

D. Có ba người là bạn của nhau

Xem đáp án

Câu 203:

Số hàm từ tập có k phần tử vào tập có n phần tử.

A. (nk)

B. (n-k)!

C. (kn)

D. (n! / k!)

Xem đáp án

Câu 204:

Hoán vị nào dưới đây là hoán vị kế tiếp của hoán vị 2 1 3 4 5 6 7 8 9.

A. 2 3 1 4 5 6 7 8 9

B. 2 1 4 3 5 6 7 8 9

C. 2 1 3 4 5 6 7 9 8

D. 3 1 2 4 5 6 7 8 9

Xem đáp án

Câu 205:

Cho n, r là các số nguyên không âm sao cho r ≤ n r ≤ n . Khi đó:

A. C(n,r) = C(n+r-1,r)

B. C(n,r) = C(n, r-1)

C. C(n,r) = C(n,n-r)

D. C(n,r) = C(n-r,r)

Xem đáp án

Câu 206:

Thuật toán được định nghĩa:

A. Là một dãy các bước mỗi bước mô tả các thao tác được thực hiên để giải quyết bài toán

B. Là một dãy vô hạn các bước mỗi bước mô tả các thao tác được thực hiên để giải quyết bài toán ban đầu.

C. Là một dãy hữu hạn các bước, mỗi bước mô tả chính sách các phép toán hoặc hành động cần thực hiện để giải quyết một vấn đề.

D. Là một dãy tuần tự các bước được thực hiên để giải quyết bài toán

Xem đáp án

Câu 207:

Khi xây dựng một thuật toán cần chú ý đến các đặc trưng sau đây:

A. Nhập, xuất, tính xác định, tính hữu hạn, tính hiệu quả, tính đúng đắn

B. Nhập, xuất, tính xác định, tính hiệu quả, tính tổng quát, tính đúng đắn

C. Nhập, xuất, tính xác định, tính hữu hạn, tính hiệu quả, tính tổng quát, tính đúng đắn.

D. Xuất, tính xác định, tính hữu hạn, tính hiệu quả, tính tổng quát, tính đúng đắn

Xem đáp án

Câu 208:

Các phương pháp thường dùng để biểu diễn thuật toán trước khi viết chương trình là:

A. Dùng ngôn ngữ tự nhiên, dùng ngôn ngữ lập trình, viết chương trình

B. Dùng sơ đồ khối, dùng ngôn ngữ lập trình, viết chương trình

C. Dùng ngôn ngữ tự nhiên, dùng ngôn ngữ lập trình, dùng mã nhị phân

D. Dùng ngôn ngữ tự nhiên, dùng sơ đồ khối, dùng giả mã

Xem đáp án

Câu 209:

Liệt kê là phương pháp:

A. Đưa ra một công thức cho lời giải bài toán

B. Chỉ ra nghiệm tốt nhất theo một nghĩa nào đó của bài toán.

C. Đưa ra danh sách tất cả các cấu hình tổ hợp có thể có.

D. Chỉ ra một nghiệm hoặc chứng minh bài toán không có nghiệm

Xem đáp án

Câu 210:

Một thuật toán liệt kê phải đảm bảo:

A. Không duyệt các cấu hình không thuộc tập các cấu hình

B. Không bỏ xót và không lặp lại bất kì một cấu hình nào

C. Không bỏ xót một cấu hình nào

D. Không duyệt lại các cấu hình đã duyệt

Xem đáp án

Câu 211:

Định nghĩa bằng đệ qui là phương pháp:

A. Định nghĩa đối tượng thông qua chính nó.

B. Định nghĩa đối tượng thông qua các đối tượng trừu tượng

C. Định nghĩa đối tượng thông qua các đối tượng đã xác định

D. Định nghĩa đối tượng thông qua các đối tượng khác

Xem đáp án

Câu 212:

Nội dung chính của thuật toán quay lui là:

A. Xây dựng toàn bộ các thành phần của cấu hình bằng cách thử tất cả các khả năng

B. Xây dựng dần các thành phần của cấu hình bằng cách thử tất cả các khả năng.

C. Xây dựng mỗi thành phần của cấu hình bằng cách thử tất cả các khả năng

D. Xây dựng bất kì thành phần nào của cấu hình bằng cách thử tất cả các khả năng

Xem đáp án

Câu 213:

Thuật toán được qọi là đệ quy nếu:

A. Giải quyết bài toán bằng cách chia nhỏ bài toán ban đầu tới các bài toán cơ sở

B. Giải quyết bài toán bằng cách chia đôi bài toán ban đầu thành các bài toán con

C. Giải quyết bài toán bằng cách rút gọn liên tiếp bài toán ban đầu tới bài toán cũng như vậy nhưng có dữ liệu đầu vào nhỏ hơn.

D. Giải quyết bài toán bằng cách rút gọn liên tiếp bài toán ban đầu tới bài toán cũng như vậy nhưng có dữ liệu đầu vào bằng một nửa.

Xem đáp án

Câu 214:

Cấu trúc của chương trình con đệ quy gồm:

A. Phần dễ giải quyết và phần khó giải quyết

B. Phần cơ sở và phần đệ quy

C. Phần cơ sở và phần quy nạp

D. Phần hữu hạn và phần quy nạp

Xem đáp án

Câu 215:

Nội dung của nguyên lý cộng phát biểu trên hai tập hợp hữu hạn A, B:

A. Nếu có N đồ vật được đặt vào K hộp thì sẽ tồn tại một hộp chứa ít nhất đồ vật.

B. Nếu A và B là hai tập hợp rời nhau thì: N( A+B )= N(A) + N(B)

C. Nếu A và B là hai tập hợp thì: N(A+B)= N(A) + N(B) – N(A+B)

D. Nếu A và B là hai tập hợp thì: N(A.B ) = N(A).N(B)

Xem đáp án

Câu 216:

Nội dung của nguyên lý bù trừ phát biểu trên hai tập hợp hữu hạn A, B:

A. Nếu A và B là hai tập hợp rời nhau thì: N( A+B )= N(A) + N(B)

B. Nếu A và B là hai tập hợp thì: N(A . B ) = N(A).N(B)

C. Nếu A và B là hai tập hợp thì: N(A+B)= N(A) + N(B) – N(A+B)

D. Nếu có N đồ vật được đặt vào K hộp thì sẽ tồn tại một hộp chứa ít nhất đồ vật.

Xem đáp án

Câu 217:

Nội dung của nguyên lý nhân phát biểu trên hai tập hợp hữu hạn A, B:

A. Nếu A và B là hai tập hợp thì: N(A . B) = N(A).N(B)

B. Nếu A và B là hai tập hợp thì: N(A+B)= N(A) + N(B) – N(A+B)

C. Nếu A và B là hai tập hợp rời nhau thì: N( A+B )= N(A) + N(B)

D. Nếu có N đồ vật được đặt vào K hộp thì sẽ tồn tại một hộp chứa ít nhất đồ vật.

Xem đáp án

Câu 218:

Các hoán vị của n phần tử:

A. Là một bộ không kể thứ tự gồm k thành phần khác nhau lấy từ n phần tử đã cho.

B. Là bộ có thứ tự gồm k thành phần lấy ra từ n phần tử đã cho. Các phần tử không được lặp lại.

C. Là một cách xếp có thứ tự n phần tử đó thành một dãy.

D. Là bộ có thứ tự gồm k thành phần lấy từ n phần tử của tập đã cho.

Xem đáp án

Câu 219:

Chỉnh hợp không lặp chập k của n phần tử:

A. Là một bộ không kể thứ tự gồm k thành phần khác nhau lấy từ n phần tử đã cho.

B. Là bộ có thứ tự gồm k thành phần lấy từ n phần tử của tập đã cho.

C. Là bộ có thứ tự gồm k phần tử khác nhau lấy ra từ n phần tử đã cho. Các phần tử không được lặp lại.

D. Là một cách xếp có thứ tự n phần tử đó.

Xem đáp án

Câu 220:

Một chỉnh hợp lặp chập k của n phần tử:

A. Là bộ có thứ tự gồm k thành phần lấy ra từ n phần tử đã cho. Các phần tử không được lặp lại.

B. Là bộ có thứ tự gồm k thành phần lấy từ n phần tử của tập đã cho.

C. Là một bộ không kể thứ tự gồm k thành phần khác nhau lấy từ n phần tử đã cho.

D. Là một cách xếp có thứ tự n phần tử đó.

Xem đáp án

Câu 221:

Một tổ hợp chập k của n phần tử:

A. Là một cách xếp có thứ tự n phần tử đó

B. Là một bộ không kể thứ tự gồm k thành phần khác nhau lấy từ n phần tử đã cho.

C. Là bộ có thứ tự gồm k thành phần lấy từ n phần tử của tập đã cho.

D. Là bộ có thứ tự gồm k thành phần lấy ra từ n phần tử đã cho. Các phần tử không được lặp lại.

Xem đáp án

Câu 222:

Số các các chỉnh hợp lặp chập k của n là:

A. n!

B. n! / k!(n-k)!

C. Nk

D. n!/(n-k)!

Xem đáp án

Câu 223:

Số các các chỉnh hợp không lặp chập k của n là:

A. Nk

B. n! / k!(n-k)!

C. n!/(n-k)!

D. n!

Xem đáp án

Câu 224:

Số các các chỉnh hợp không lặp chập k của n là:

A. Nk

B. n! / k!(n-k)!

C. n!/(n-k)!

D. n!

Xem đáp án

Câu 225:

Số các các hoán vị của tập n phần tử là:

A. n!/(n-k)!

B. n! / k!(n-k)!

C. Nk

D. n!

Xem đáp án

Câu 226:

Số các tổ hợp chập k của tập n phần tử là:

A. n!

B. Nk

C. n!/(n-k)!

D. n! / k!(n-k)!

Xem đáp án

Câu 227:

Số tổ hợp lặp chập r từ tập n phần tử bằng:

A. C(n+r,r)

B. C(n+r+1,r)

C. C(n+r-1,r-1)

D. C(n+r-1,r)

Xem đáp án

Câu 228:

Cho C = { 2, 4, 5, 6, 7, 8}, k = 6, n=9. Kết quả nào đúng trong số những kết quả dưới đây sau khi thực hiện thuật toán Test(C, k, n):

Function Test(C:array[1..10] of integer; k,n:integer);

Var i,j: integer;

Begin

i:=k; While (i>0) and (c[i]=n-k+i) do i:=i-1;

If i> 0 then

Begin c[i]:= c[i] +1;

For j:= i+1 to k do c[j]:=c[i] + j-1;

End;

End;

A. C= {2, 4, 5, 6, 7, 9}

B. C= {4, 5, 6, 7, 8, 9}

C. C= {3, 4, 5, 6, 7, 8}

D. C= {3, 5, 6, 7, 8, 9}

Xem đáp án

Câu 229:

Kết quả nào đúng trong số những kết quả dưới đây sau khi thực hiện thuật toán:

Function Test (n: Integer): Integer;

Var f1, f2, fn: Integer;

Begin

f1=1;

f2=1;

i:=3;

While i<=n do

Begin

fn := f1 + f2; f1:=f2; f2:=fn;

i:=i+1;

End;

Test:= fn;

End;

A. Test(6) = 5

B. Test(5) = 3

C. Test(7) = 13

D. Test(4) = 1

Xem đáp án

Câu 230:

Cho B = { 1, 0, 1, 0, 1, 0, 1, 1, 1, 0}, n=10. Kết quả nào đúng trong số những kết quả dưới đây sau khi thực hiện thuật toán:

Type Mang= array[1..10] of Integer;

Function Test(B:mang; n:integer): mang;

Var i:integer;

Begin

i:=n-1;

While (i>=0) and (B[i]=1) do

Begin B[i]:=0; i:=i-1; End;

B[i]:= 1;

End;

A. Test(B,n) = { 1, 0, 1, 0, 1, 1, 0, 0, 0, 1(0)}

B. Test(B,n) = { 1, 0, 1, 0, 1, 0, 1, 1, 1, 1}

C. Test(B,n) = { 0, 1, 1, 0, 1, 0, 1, 1, 1, 0}

D. Test(B,n) = { 1, 1, 1, 0, 1, 0, 1, 1, 1, 0}

Xem đáp án

Câu 231:

Xác định giá trị của k sau khi đoạn chương trình sau được thưc hiện xong:

k := 1;

For i1 :=1 to n1 do

k:= k+1;

For i2 :=1 to n2 do

k:= k+1;

…

For im :=1 to nm do

k:= k+1

A. n1 + n2 + … + nm

B. 1 + n1 + n2 + … + nm

C. n1 n2 … nm

D. 1+ n1 n2 … nm

Xem đáp án

Câu 232:

Xác định giá trị của k sau khi đoạn chương trình sau được thưc hiện xong:

k := 1;

For i1 :=1 to n1 do

For i2 :=1 to n2 do

…

For im :=1 to nm do

k:= k+1;

A. n1 n2 … nm

B. 1 + n1 + n2 + … + nm

C. 1+ n1 n2 … nm

D. n1 + n2 + … + nm

Xem đáp án

Câu 233:

Khi chạy chương trình:

Var S, i, j : Integer;

Begin

S := 0;

for i:= 1 to 3 do

for j:= 1 to 4 do S := S + 1 ;

End.

Giá trị sau cùng của S là:

A. 4

B. 3

C. 12

D. 0

Xem đáp án

Câu 234:

Cho S và i biến kiểu nguyên. Khi chạy đoạn chương trình:

S:= 0;

i:= 1;

while i<= 6 do

begin

S:= S + i;

i:= i + 2;

end;

Giá trị sau cùng của S là:

A. 6

B. 9

C. 11

D. 0

Xem đáp án

Câu 235:

Cho m, n, i là các biến nguyên. Khi chạy đoạn chương trình:

m:=4; n:=5; i:=5;

Repeat

i:=i+1;

Until (i Mod m = 0) and (i Mod n = 0);

Giá trị sau cùng của i là:

A. 20

B. 5

C. 4

D. 0

Xem đáp án

Câu 236:

Giả sử các khai báo biến đều hợp lệ. Ðể tính S = 10!, chọn câu nào?

A. S := 1; i := 1; while i<= 10 do S := S * i; i := i + 1;

B. S := 1; i := 1; while i<= 10 do i := i + 1; S := S * i;

C. S := 0; i := 1; while i<= 10 do begin S := S * i; i := i + 1; end;

D. S := 1; i := 1; while i<= 10 do begin S := S * i; i := i + 1; end;

Xem đáp án

Câu 237:

Thuật toán đệ quy dưới đây:

Function dequy(a: real; n:integer);

Begin

If n = 0 then dequy:=1

Else dequy:= a* dequy (a,n-1);

End;

A. Tính an

B. Tính (n-1)a

C. Tính an-1

D. Tính na

Xem đáp án

Câu 238:

Cho thuật toán đệ quy:

Function dequy(a: real; n:integer);

Begin

If n = 0 then dequy:=1

Else dequy:= a* dequy (a,n-1);

End;

Kết quả nào trong các kết quả sau là đúng?

A. Dequy(2,5) = 10

B. Dequy(2,5) = 25

C. Dequy(5,2) = 25

D. Dequy(5,2) = 10

Xem đáp án

Câu 239:

Kết quả nào đúng trong số những kết quả dưới đây sau khi thực hiện thuật toán:

Function Test (n:integer):longint;

Begin

If n = 0 then Test:=1

Else Test:= n * Test(n-1);

End;

A. Test(4) = 24

B. Test(2) = 1

C. Test(3) = 9

D. Test(5) = 20

Xem đáp án

Câu 240:

Thuật toán đệ qui dưới đây tính:

Function Test (a,b: integer): integer;

Begin

If a = 0 then Test:=b

Else Test:= Test(b mod a, a);

End;

A. Ước số chung lớn nhất của hai số a và b.

B. Số nhỏ nhất trong hai số a và b.

C. Bội số chung nhỏ nhất của a và b.

D. Số lớn nhất trong hai số a và b.

Xem đáp án

Câu 241:

Thuật toán đệ qui dưới đây tính:

Function Test (n:integer):longint;

Begin

If n = 0 then Test:=1

Else Test:= n * Test(n-1);

End

A. Tích số của n số n.

B. Tích số của n số tự nhiên đầu tiên.

C. Tích số của n-1 số n.

D. Tích số của n-1 số tự nhiên đầu tiên

Xem đáp án

Câu 242:

Thuật toán đệ qui dưới đây tính:

Function Tesr(n:integer): integer;

Begin

If n<=2 then Test:=1

Else Test: = Test (n-1) + Test (n-2);

End;

A. Tổng n số tự nhiên đầu tiên.

B. Số Fibonacci thứ n.

C. Số nguyên tố thứ n.

D. Tổng hai số nguyên liên tiếp n và n-1.

Xem đáp án

Câu 243:

Cho thuật toán:

Procedure Test (n:integer);

Begin

If (n>0) and (n<10) then Write(n)

If n>=10 then begin

Write(n mod 10);

Test (n div 10);

End;

End;

Với n=151. Kết quả nào đúng trong số những kết quả dưới đây?

A. 1

B. 15

C. 151

D. 150

Xem đáp án

Câu 244:

Kết quả của thuật toán dưới đây:

Procedure Test (n:integer);

Begin

If (n>0) and (n<10) then Write(n)

If n>=10 then begin

Write(n mod 10);

Test (n div 10);

End;

End;

A. Đưa ra màn hình thương của n cho 10

B. Đưa ra màn hình đảo ngược số n

C. Đưa ra màn hình số dư trong phép chia của n cho 10

D. Đưa ra màn hình là n nếu n nhỏ hơn 10 và thương của n cho 10 nếu $n \geq 10$

Xem đáp án

Câu 245:

Cho thuật toán:

Procedure Test(x,i,j: Integer);

Var m:integer;

Begin

m:=trunc(i+j)/2;

If x= a[i] then vt:=m

Else If (x<a[m]) and ( i<m) then Test(x,i,m-1)

Else If ( x> a[m] ) and (j>m) then Test(x,m+1,j)

Else vt:=0;

End;

Với A = {5, 2, 9 ,8, 6, 4, 7,1}. Kết quả nào đúng trong số những kết quả dưới đây:

A. Test(3,1,8), vt = 0;

B. Test(4,1,8), vt = 5;

C. Test(6,1,8), vt = 0;

D. Test(7,1,8), vt = 8;

Xem đáp án

Câu 246:

Kết quả thuật toán đệ quy:

Function Test(st:string):string;

Begin

If length(st) <=1 then Test:=st

Else Test:= st[length(st)] + Test(Copy(st,1,length(st)-1));

End;

A. Xuất mỗi kí tự của st trên một dòng

B. Đảo ngược chuỗi st

C. Đưa ra tất cả các xâu con của xâu kí tự st

D. Đưa ra độ dài của xâu st

Xem đáp án

Câu 247:

Thuật toán đệ quy dưới đây tính:

Function Test(a,b:Integer): Integer;

Begin

If (a=0) or (b=0) then Test:=a+b

Else

If a > b then Test:=Test(a-b,b)

Else Test:= Test(a,b-a);

End;

A. Tính hiệu 2 số a và b

B. Tìm số dư trong phép chia a cho b

C. Tìm ước chung lớn nhất của a và b

D. Tìm bội chung nhỏ nhất của a và b

Xem đáp án

Câu 248:

Cho thuật toán:

Function Test(a,b:Integer): Integer;

Begin

If (a=0) or (b=0) then Test:=a+b

Else

If a > b then Test:=Test(a-b,b)

Else Test:= Test(a,b-a);

End;

Với a = 81, b = 54. Kết quả nào đúng trong số những kết quả dưới đây:

A. 81

B. 27

C. 1

D. 9

Xem đáp án

Câu 249:

Thuật toán đệ quy dưới đây tính:

Function Test(a,b): Integer;

Begin

If (b = a) or (b = 0) then Test:=1

Else Test := Test (a-1,b-1) + Test (a-1,b);

End;

A. Bội chung nhỏ nhất của a và b

B. Ước chung lớn nhất của a và b

C. Số Fibonaci thứ a

D. Tổ hợp chập b của a

Xem đáp án

Câu 250:

Cho thuật toán:

Function Test(a,b): Integer;

Begin

If (b = a) or (b = 0) then Test:=1

Else Test := Test (a-1,b-1) + Test (a-1,b);

End;

Với a = 21, b = 3. Kết quả nào đúng trong số những kết quả dưới đây:

A. 10946

B. 1330

C. 3

D. 21

Xem đáp án

Câu 251:

Từ bảng chữ cái tiếng Anh có thể tạo ra được bao nhiêu xâu kí tự có độ dài N.

A. 26.(N-1)

B. 26N

C. N26

D. 26N

Xem đáp án

Câu 252:

Cho tập X = { 1, 2, . ., 10000} có bao nhiêu số không chia hết cho bất cứ số nào trong các số 3, 4, 7.

A. 4286

B. 7260

C. 7261

D. 727

Xem đáp án

Câu 253:

Có năm loại học bổng khác nhau để phát cho sinh viên. Hỏi phải có ít nhất bao nhiêu sinh viên để chắc chắn có 5 người được nhận học bổng như nhau.

A. Có ít nhất 52 sinh viên.

B. Có ít nhất 5 sinh viên

C. Có ít nhất 26 sinh viên.

D. Có ít nhất 50 sinh viên

Xem đáp án

Câu 254:

Có bao nhiêu số nguyên không lớn hơn 1000 chia hết cho 7 hoặc 11?

A. 200

B. 120

C. 220

D. 20

Xem đáp án

Câu 255:

Có bao nhiêu xâu nhị phân có độ dài nhỏ hơn hoặc bằng 8 bắt đầu là bít 1?

A. 1+21 + 22 + 23 + 24 + 25 + 26 + 27

B. 1+21 + 22 + 23 + 24 + 25 + 26 + 27 + 28

C. 21 + 22 + 23 + 24 + 25 + 26 + 27 + 28

D. 21 + 22 + 23 + 24 + 25 + 26 + 27

Xem đáp án

Câu 256:

Trong bất kỳ 27 từ tiếng Anh nào cũng đều có:

A. Ít nhất một từ cùng bắt đầu bằng một chữ cái.

B. Nhiều nhất hai từ cùng bắt đầu bằng một chữ cái.

C. Ít nhất hai từ cùng bắt đầu bằng một chữ cái.

D. Nhiều nhất một từ cùng bắt đầu bằng một chữ cái.

Xem đáp án

Câu 257:

Trong 100 người có:

A. Ít nhất 9 người sinh nhật cùng một tháng.

B. Nhiều nhất 9 người sinh nhật cùng một tháng.

C. Ít nhất 8 người sinh nhật cùng một tháng.

D. Ít nhất 12 người sinh nhật cùng một tháng.

Xem đáp án

Câu 258:

Có bao nhiêu xâu nhị phân có độ dài nhỏ hơn hoặc bằng 6 kết thúc là bít 0?

A. 1+21 + 22 + 23 + 24 + 25

B. 21 + 22 + 23 + 24 + 25

C. 1+21 + 22 + 23 + 24 + 25 + 26

D. 21 . 22 . 23 . 24 .25

Xem đáp án

Câu 259:

Tìm số các số nguyên dương không vượt quá 100 hoặc là số lẻ hoặc là bình phương của một số nguyên?

A. 50

B. 60

C. 55

D. 65

Xem đáp án

Câu 260:

Tìm các số nguyên không vượt quá 100 hoặc là bình phương hoặc là lập phương của một số nguyên?

A. 11

B. 10

C. 50

D. 13

Xem đáp án

Câu 261:

Có bao nhiêu phần tử trong hợp của 4 tập hợp, nếu các tập hợp tương ứng có 50, 60, 70, 80 phần tử, mỗi cặp 2 tập hợp có chung 5 phần tử, mỗi bộ 3 tập hợp có 1 phần tử chung và không có phần tử nào cùng thuộc cả 4 tập hợp.

A. 260

B. 237

C. 243

D. 234

Xem đáp án

Câu 262:

Có năm loại học bổng khác nhau để phát cho sinh viên. Hỏi phải có ít nhất bao nhiêu sinh viên để chắc chắn có 5 người được nhận học bổng như nhau.

A. Có ít nhất 52 sinh viên.

B. Có ít nhất 5 sinh viên

C. Có ít nhất 26 sinh viên.

D. Có ít nhất 50 sinh viên

Xem đáp án

Câu 263:

Cho tập X = { 1, 2, . ., 10000} có bao nhiêu số không chia hết cho bất cứ số nào trong các số 3, 4, 7.

A. 4286

B. 7260

C. 7261

D. 727

Xem đáp án

Câu 264:

Có bao nhiêu số nguyên không lớn hơn 1000 chia hết cho 7 hoặc 11?

A. 200

B. 120

C. 220

D. 20

Xem đáp án

Câu 265:

Có bao nhiêu xâu nhị phân có độ dài nhỏ hơn hoặc bằng 8 bắt đầu là bít 1?

A. 1+21 + 22 + 23 + 24 + 25 + 26 + 27

B. 1+21 + 22 + 23 + 24 + 25 + 26 + 27 + 28

C. 21 + 22 + 23 + 24 + 25 + 26 + 27 + 28

D. 21 + 22 + 23 + 24 + 25 + 26 + 27

Xem đáp án

Câu 266:

Trong bất kỳ 27 từ tiếng Anh nào cũng đều có:

A. Ít nhất một từ cùng bắt đầu bằng một chữ cái.

B. Nhiều nhất hai từ cùng bắt đầu bằng một chữ cái.

C. Ít nhất hai từ cùng bắt đầu bằng một chữ cái.

D. Nhiều nhất một từ cùng bắt đầu bằng một chữ cái.

Xem đáp án

Câu 267:

Trong 100 người có:

A. Ít nhất 9 người sinh nhật cùng một tháng.

B. Nhiều nhất 9 người sinh nhật cùng một tháng.

C. Ít nhất 8 người sinh nhật cùng một tháng.

D. Ít nhất 12 người sinh nhật cùng một tháng.

Xem đáp án

Câu 268:

Có bao nhiêu xâu nhị phân có độ dài nhỏ hơn hoặc bằng 6 kết thúc là bít 0?

A. 1+21 + 22 + 23 + 24 + 25

B. 21 + 22 + 23 + 24 + 25

C. 1+21 + 22 + 23 + 24 + 25 + 26

D. 21 . 22 . 23 . 24 .25

Xem đáp án

Câu 269:

Tìm số các số nguyên dương không vượt quá 100 hoặc là số lẻ hoặc là bình phương của một số nguyên?

A. 50

B. 60

C. 55

D. 65

Xem đáp án

Câu 270:

Tìm các số nguyên không vượt quá 100 hoặc là bình phương hoặc là lập phương của một số nguyên?

A. 11

B. 10

C. 50

D. 13

Xem đáp án

Câu 271:

Có bao nhiêu phần tử trong hợp của 4 tập hợp, nếu các tập hợp tương ứng có 50, 60, 70, 80 phần tử, mỗi cặp 2 tập hợp có chung 5 phần tử, mỗi bộ 3 tập hợp có 1 phần tử chung và không có phần tử nào cùng thuộc cả 4 tập hợp.

A. 260

B. 237

C. 243

D. 234

Xem đáp án

Câu 272:

Có bao nhiêu biển đăng ký xe nếu mỗi biển gồm 2 hoặc 3 chữ cái tiếp sau bởi 2 hoặc 3 chữ số?

A. 20077200

B. 17576000

C. 676000

D. 1757600

Xem đáp án

Câu 273:

Cô dâu và chủ rể mời 4 người bạn đứng thành một hàng để chụp ảnh với mình. Có bao nhiêu cách xếp hàng nếu cô dâu đứng cạnh chú rể?

A. 120

B. 240

C. 360

D. 480

Xem đáp án

Câu 274:

Cô dâu và chủ rể mời 4 người bạn đứng thành một hàng để chụp ảnh với mình. Có bao nhiêu cách xếp hàng nếu cô dâu không đứng cạnh chú rể?

A. 720

B. 480

C. 360

D. 240

Xem đáp án

Câu 275:

Cô dâu và chủ rể mời 4 người bạn đứng thành một hàng để chụp ảnh với mình. Có bao nhiêu cách xếp hàng nếu cô dâu đứng ở phía bên trái chú rể?

A. 120

B. 720

C. 360

D. 480

Xem đáp án

Câu 276:

Bài thi các môn học trong trường đai học được chấm theo thang điểm là các số nguyên từ 0 đến 100. Một lớp học cần phải có ít nhất bao nhiêu sinh viên để đảm bảo trong mọi môn thi đều có ít nhất 2 sinh viên nhận cùng điểm?

A. 100

B. 102

C. 101

D. 200

Xem đáp án

Câu 277:

Cần phải có tối thiểu bao nhiêu sinh viên ghi tên vào lớp Toán học rời rạc để chắc chắn rằng sẽ có ít nhất 6 người cùng đạt một điểm thi, nếu thang điểm gồm 5 bậc A, B, C, D, E, F?

A. 30

B. 26

C. 25

D. 31

Xem đáp án

Câu 278:

Giả sử có 14 sinh viên nhận được điểm A trong kỳ thi thứ nhất của môn Toán rời rạc, 18 sinh viên nhận được điểm A trong kỳ thi thứ 2. Nếu có 22 sinh viên nhận được điểm A hoặc trong kỳ thi đầu hoặc trong kỳ thi thứ 2 thì có bao nhiêu sinh viên nhận đợc điểm A trong cả hai lần thi.

A. 14

B. 8

C. 10

D. 18

Xem đáp án

Câu 279:

Có bao nhiêu cách xếp các chữ a, b, c, d, e sao cho chữ b không đi liền sau chữ a và d không đi liền sau chữ c?

A. 120

B. 78

C. 72

D. 96

Xem đáp án

Câu 280:

Một đa giác lồi n cạnh sẽ có bao nhiêu đường chéo? (Một đa giác được gọi là lồi nếu mọi đoạn thẳng nối 2 điểm bên trong hoặc trên biên nằm hoàn toàn trong nó)

A. n(n-3)/2

B. n(n-1)/2

C. 2n

D. 2n – n

Xem đáp án

Câu 281:

Trong bất kỳ một nhóm có 367 người, thế nào cũng có:

A. Nhiều nhất một người có cùng ngày sinh.

B. Ít nhất một người có cùng ngày sinh.

C. Ít nhất hai người có cùng ngày sinh.

D. Nhiều nhất một người có cùng ngày sinh.

Xem đáp án

Câu 282:

Một người gửi 10.000 Đôla vào tài khoản của mình tại một ngân hàng với lãi suất kép 11% mỗi năm. Hỏi sau 30 năm anh ta có bao nhiêu tiền trong tài khoản của mình?

A. (1.11)29. 10.000

B. (1.11)30 . 10.000

C. (0.11)30 .10.000

D. (0.1)30.10.000

Xem đáp án

Câu 283:

Có n lá thư và n phong bì ghi sẵn địa chỉ. Bỏ ngẫu nhiên các lá thư vào các phong bì. Hỏi xác suất để xảy ra không một Là thư nào bỏ đúng địa chỉ là bao nhiêu?

A. (1/n) *(e/n)

B. e-1

C. e/n

D. 1/n

Xem đáp án

Câu 284:

Có bao nhiêu xâu nhị phân có độ dài N.

A. N(N-1)/2

B. N2

C. 2N

D. 2.(N-1)

Xem đáp án

Câu 285:

Cần bố trí thực hiện N chương trình trên một máy tính. Hỏi có bao nhiêu cách bố trí khác nhau.

A. N!

B. N(N-1) /2

C. NN

D. N2

Xem đáp án

Câu 286:

Lớp toán học rời rạc có 25 sinh viên giỏi tin học, 13 sinh viên giỏi toán và 8 sinh viên giỏi cả toán và tin học. Hỏi lớp có bao nhiêu sinh viên nếu mỗi sinh viên hoặc giỏi toán hoặc học giỏi tin học hoặc giỏi cả hai môn?

A. 12

B. 25

C. 30

D. 13

Xem đáp án

Câu 287:

Một hội nghị bàn tròn của phái đoàn các nước: Việt Nam 3 người; Lào 2 người; Campuchia 1 người; Thái Lan 2 người. Có bao nhiêu cách xếp chỗ ngồi cho mọi thành viên sao cho người cùng quốc tịch ngồi cạnh nhau?

A. 120

B. 476

C. 24

D. 96

Xem đáp án

Câu 288:

Một thương nhân đi bán hàng tại n thành phố. Chị ta có thể bắt đầu hành trình của mình tại một thành phố nào đó nhưng phải qua (n-1) thành phố kia theo bất kỳ thứ tự nào mà chị muốn. Hỏi có bao nhiêu lộ trình khác nhau chị ta có thể đi?

A. (n!)

B. (n (n-1))/2

C. (n (n-1))

D. (n-1)!

Xem đáp án

Câu 289:

Một dự án đánh số điện thoại có dạng NYX NNX XXXX.Trong đó, X là các số từ 0 đến 9 , Y là các số hoặc 0 hoặc 1, N là các số từ 2 đến 9, hỏi có nhiều nhất là bao nhiêu số điện thoại khác nhau được đánh số?

A. 64. 106

B. 1024. 106

C. 8.106

D. 512.106

Xem đáp án

Câu 290:

Có bao nhiêu xâu nhị phân độ dài 8 chứa ít nhất 3 số 0 và ít nhất 3 số 1?

A. 112

B. 912

C. 182

D. 120

Xem đáp án

Câu 291:

Phương trình x₁ + x₂ + x₃ = 11 có bao nhiêu nghiệm nguyên không âm?

A. 78

B. 165

C. 990

D. 21

Xem đáp án

Câu 292:

Có thể nhận bao nhiêu xâu khác nhau bằng cách sắp xếp lại các chữ cái của từ success.

A. 5040

B. 420

C. 70

D. 10290

Xem đáp án

Câu 293:

Ngôn ngữ Pascal chuẩn quy định đặt tên biến không quá 8 kí tự, các kí tự trong tên biến chỉ là các chữ cái từ a..z hoặc các chữ số từ 0..9 và phải bắt đầu bằng chữ cái. Có bao nhiêu tên biến khác nhau thỏa mãn yêu cầu trên?

A. 26(1+261 + 262 + … + 267)

B. 1+261 + 262 + … + 267

C. 261 + 262 + … + 267

D. 361 + 362 + … + 368

Xem đáp án

Câu 294:

Cho A={1,2,3,4,5}. Có bao nhiêu số tự nhiên gồm 5 chữ số khác nhau bắt đầu bởi chữ số 5 được thành lập từ A.

A. 24

B. 96

C. 120

D. 5

Xem đáp án

Câu 295:

Cho A={1,2,3,4,5}. Có bao nhiêu số tự nhiên gồm 5 chữ số khác nhau không bắt đầu bởi chữ số 1 được thành lập từ A.

A. 24

B. 120

C. 96

D. 16

Xem đáp án

Câu 296:

Cho A={1,2,3,4,5}. Có bao nhiêu số tự nhiên gồm 5 chữ số khác nhau bắt đầu bởi chữ số 5 không kết thúc bởi chữ số 1 được thành lập từ A.

A. 24

B. 16

C. 6

D. 18

Xem đáp án

Câu 297:

Một đơn vị lúc bắt đầu thành lập có 14 người. Cần chọn ra một người làm trưởng phòng, một người làm phó phòng, một người làm kế toán trưởng. Hỏi có bao nhiêu cách chọn mà không ai làm kiêm nhiệm?

A. 1001

B. 2184

C. 364

D. 512

Xem đáp án

Câu 298:

Có bao nhiêu chuỗi bít có độ dài nhỏ hơn hoặc bằng 6?

A. 64

B. 124

C. 126

D. 62

Xem đáp án

Câu 299:

Có một bàn tròn, xung quanh gồm 2n chiếc ghế. Cần sắp chỗ cho n cặp vợ chồng sao cho: các ông ngồi xen kẽ các bà và các cặp vợ chồng ngồi cạnh nhau. Có bao nhiêu cách sắp xếp theo yêu cầu trên?

A. N!

B. n.n!

C. 2n!

D. 4n!

Xem đáp án

Câu 300:

Một gia đình có 7 người con, trong đó có một nhóm sinh 3, một nhóm sinh đôi và 2 nhóm sinh 1. Những đứa trẻ sinh đôi và sinh 3 giống nhau như đúc. Có bao nhiêu cách sắp xếp bọn trẻ thành một dãy.

A. 70

B. 420

C. 5040

D. 44

Xem đáp án

Câu 301:

Có bao nhiêu số nguyên dương gồm đúng 3 chữ số và chia hết cho 7?

A. 128

B. 96

C. 24

D. 32

Xem đáp án

Câu 302:

Có bao nhiêu số nguyên dương gồm đúng 3 chữ số chia hết cho 3 và chia hết cho 4?

A. 300

B. 75

C. 224

D. 449

Xem đáp án

Câu 303:

Có bao nhiêu số nguyên dương gồm đúng 3 chữ số chia hết cho 3 nhưng không chia hết cho 4?

A. 300

B. 224

C. 76

D. 75

Xem đáp án

Câu 304:

Có bao nhiêu số nguyên dương gồm đúng 3 chữ số chia hết cho 3 hoặc chia hết cho 4?

A. 75

B. 300

C. 224

D. 449

Xem đáp án

Câu 305:

Cho tập nền A = {4, 5, 6, 7, 8}. Có bao nhiêu số có 3 chữ số khác nhau là số chẵn được thành lập từ A.

A. 180

B. 36

C. 18

D. 60

Xem đáp án

Câu 306:

Cho A = {1,2,3,4,5,6,7}. Có bao nhiêu số tự nhiên gồm 5 chữ số khác nhau bắt đầu bởi chữ số 4 được thành lập từ A.

A. 840

B. 360

C. 2520

D. 2401

Xem đáp án

Câu 307:

Cho các số {1, 2, 3, 4, 5, 6, 7}. Tìm các số tự nhiêm gồm 5 chữ số lấy từ tập trên sao cho không tận cùng bằng chữ số 5.

A. 14406

B. 16807

C. 2401

D. 840

Xem đáp án

Câu 308:

Với 10 chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ta có thể lập nên bao nhiêu số khác nhau thoả mãn các điều kiện sau:

- Mỗi chữ số phải có mặt một lần trong số lập nên.

- Chữ số 1 không đứng ở vị trí thứ nhất

A. 3628800

B. 3265920

C. 362880

D. 326592

Xem đáp án

Câu 309:

Cho A = {0,1,2,3,4,5,6}. Có bao nhiêu số tự nhiên gồm 5 chữ số khác nhau được thành lập từ A.

A. 2520

B. 2160

C. 360

D. 36

Xem đáp án

Câu 310:

Người ta xếp ngẫu nhiên 5 lá phiếu có ghi số thứ tự từ 1 đến 5 cạnh nhau. Có bao nhiêu cách xếp để các phiếu số chẵn luôn ở cạnh nhau?

A. 120

B. 24

C. 36

D. 48

Xem đáp án

Câu 311:

Chín đồ chơi có thể được chia bao nhiêu cách cho 4 bé nếu bé nhỏ nhất nhận 3 đồ chơi và mỗi bé còn lại nhận 2 đồ chơi?

A. 15120

B. 7560

C. 118

D. 666

Xem đáp án

Câu 312:

Một nông dân mua 3 con bò, 2 con heo, 4 con gà từ một người có 6 con bò, 5 con heo và 8 con gà. Người nông dân này sẽ có bao nhiêu sự lựa chọn?

A. 14000

B. 110

C. 2100

D. 1820

Xem đáp án

Câu 313:

Một nhóm 7 người có thể tự sắp theo bao nhiêu cách xung quanh một bàn tròn?

A. 7!

B. 6.6!

C. 6!

D. 7!-6

Xem đáp án

Câu 314:

Một học viên phải trả lời 8 trong số 10 câu hỏi cho một kỳ thi. Học viên này có bao nhiêu sự lựa chọn nếu học viên phải trả lời 3 câu hỏi đầu tiên?

A. 21

B. 252

C. 186

D. 63

Xem đáp án

Câu 315:

Người ta xếp ngẫu nhiên 5 lá phiếu có ghi số thứ tự từ 1 đến 5 cạnh nhau. Có bao nhiêu cách xếp để các phiếu phân thành 2 nhóm chẵn lẻ riêng biệt.

A. 2

B. 20

C. 10

D. 24

Xem đáp án

Câu 316:

Một đa giác lồi n cạnh sẽ có bao nhiêu đường chéo? (Một đa giác được gọi là lồi nếu mọi đoạn thẳng nối 2 điểm bên trong hoặc trên biên nằm hoàn toàn trong nó).

A. n(n-3)/2

B. n(n-1)/2

C. n!/2

D. (n!-n)/2

Xem đáp án

Câu 317:

Giả sử một tổ bộ môn có 10 nam và 15 nữ. Có bao nhiêu cách chọn một hội đồng gồm 6 uỷ viên trong đó số uỷ viên nam bằng số uỷ viên nữ?

A. 455

B. 177100

C. 54600

D. 5215

Xem đáp án

Câu 318:

Có bao nhiêu xâu nhị phân độ dài 10 bắt đầu bởi 00 hoặc kết thúc bởi 11.

A. 24

B. 448

C. 84

D. 8

Xem đáp án

Câu 319:

Có bao nhiêu chuỗi bít độ dài bằng 8 hoặc bắt đầu bởi 00 hoặc kết thúc bởi 11.

A. 112

B. 128

C. 64

D. 124

Xem đáp án

Câu 320:

Có bao nhiêu xâu nhị phân độ dài bằng 8 bắt đầu bởi 00 và kết thúc bởi 11?

A. 64

B. 32

C. 96

D. 128

Xem đáp án

Câu 321:

Một học viên phải trả lời 8 trong số 10 câu hỏi cho một kỳ thi. Học viên này có bao nhiêu sự lựa chọn nếu học viên phải trả lời ít nhất 4 trong 5 câu hỏi đầu tiên?

A. 75

B. 35

C. 45

D. 30

Xem đáp án

Câu 322:

Có 12 học viên trong một lớp. Có bao nhiêu cách để 12 học viên có 3 bài kiểm tra khác nhau nếu 4 học viên có chung mỗi bài kiểm tra?

A. 34650

B. 220

C. 3465

D. 650

Xem đáp án

Câu 323:

Nếu G = (V,E) là một đồ thị vô hướng thì:

A. Số đỉnh bậc lẻ và số đỉnh bậc chẵn là một số chẵn

B. Số đỉnh bậc chẵn là một số chẵn

C. Số đỉnh bậc lẻ là một số chẵn

D. Số đỉnh bậc lẻ là một số lẻ

Xem đáp án

Câu 324:

Những đơn đồ thị vô hướng nào dưới đây tồn tại nếu bậc của các đỉnh lần lượt là:

A. 1, 4, 3, 2, 5, 6.

B. 2, 1, 5, 2, 3, 3.

C. 2, 4, 3, 4, 3, 2.

D. 1, 4, 3, 2, 2, 3.

Xem đáp án

Câu 325:

Đơn đồ thị vô hướng nào dưới đây tồn tại nếu bậc của các đỉnh lần lượt là:

A. 1, 2, 3, 4, 5.

B. 0, 1, 2, 2, 3.

C. 3, 4, 3, 4, 3.

D. 1, 2, 3, 4, 7.

Xem đáp án

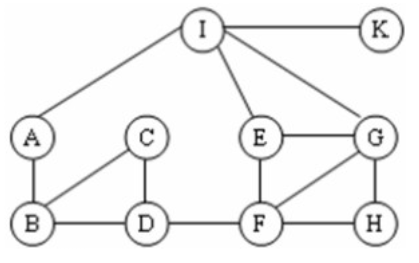
Câu 326:

Đồ thị liên thông nào trong các đồ thị dưới đây là đồ thị Euler nếu số bậc của các đỉnh lần lượt là:

A. 2, 4, 1, 2, 6

B. 3, 4, 4, 2, 4

C. 1, 4, 2, 5, 2

D. 4, 4, 6, 5, 3

Xem đáp án

Câu 327:

Trong cách biểu diễn đồ thị bằng danh sách cạnh chúng ta lưu trữ:

A. Danh sách tất cả các cạnh.

B. Danh sách tất cả các đỉnh

C. Danh sách tất cả các cạnh và các đỉnh.

D. Không lưu trữ danh sách cạnh và đỉnh nào.

Xem đáp án

Câu 328:

Trong biểu diễn đồ thị bằng danh sách kề, mỗi danh sách kề chứa:

A. Các cạnh kề với một đỉnh.

B. Các đỉnh kề với một đỉnh.

C. Tất cả các đỉnh kề và cạnh kề với nó.

D. Các bậc của đỉnh kề với một đỉnh.

Xem đáp án

Câu 329:

Tổng tất cả các bậc trong một đồ thị vô hướng bằng:

A. Hai lần số cạnh.

B. Hai lần số đỉnh.

C. Trung bình cộng của số đỉnh và số cạnh.

D. Tổng của số đỉnh và số cạnh.

Xem đáp án

Câu 330:

Nếu bậc của mỗi đỉnh trong đồ thị đều chẵn thì:

A. Đồ thị là liên thông.

B. Đồ thị không liên thông.

C. Tính liên thông của đồ thị không xác định.

D. Đồ thị là liên thông mạnh

Xem đáp án

Câu 331:

Cho đồ thị vô hướng G = (V,E), khẳng định nào sau đây là đúng?

A. Thuật toán DFS(u) duyệt tất cả các đỉnh của đồ thị trong cùng thành phần liên thông với đỉnh u

B. Thuật toán DFS(u) luôn tìm ra được đường đi giữa hai đỉnh bất kì của đồ thị

C. Thuật toán DFS(u) duyệt tất cả các thành phần liên thông của đồ thị

D. Thuật toán DFS(u) duyệt tất cả các đỉnh của đồ thị mỗi đỉnh đúng một lần

Xem đáp án

Câu 332:

Cho đồ thị vô hướng G = (V,E), khẳng định nào dưới đây là đúng?

A. Thuật toán BFS(u) duyệt tất cả các thành phần liên thông của đồ thị

B. Thuật toán BFS(u) luôn tìm ra được đường đi giữa hai đỉnh bất kì của đồ thị

C. Thuật toán BFS(u) duyệt tất cả các đỉnh của đồ thị trong cùng thành phần liên thông với đỉnh u

D. Thuật toán BFS(u) duyệt tất cả các đỉnh của đồ thị mỗi đỉnh đúng một lần

Xem đáp án

Câu 333:

Đồ thị K4 có số đỉnh và số cạnh tương ứng là?

A. 4,6

B. 4,8

C. 5,8

D. 4,4

Xem đáp án

Câu 334:

Phát biểu nào sau đây là sai khi nói đến đồ thị phân đôi đầy đủ Km,n.

A. Có tập đỉnh được phân thành hai tập con tương ứng có m đỉnh và n đỉnh.

B. Có một cạnh giữa hai đỉnh nếu và chỉ nếu một đỉnh thuộc tập con này và đỉnh thứ hai thuộc tập con kia.

C. Có một cạnh giữa hai đỉnh nếu và chỉ nếu mỗi đỉnh đều thuộc vào hai tập đỉnh con.

D. Có m+n đỉnh, mn cạnh.

Xem đáp án

Câu 335:

Đồ thị có đường đi vô hướng Euler khi và chỉ khi:

A. Liên thông và có hai đỉnh bậc lẻ.

B. Không liên thông và có hai đỉnh bậc lẻ.

C. Liên thông và có một đỉnh bậc lẻ.

D. Không liên thông và không có đỉnh bậc lẻ.

Xem đáp án

Câu 336:

Đồ thị phân đôi đầy đủ Kn,m có số màu bằng:

A. 3

B. 4

C. 2

D. -2

Xem đáp án

Câu 337:

Đường đi Euler vô hướng trên một đồ thị có đỉnh đầu và đỉnh cuối:

A. Trùng nhau

B. Khác nhau

C. Có cùng bậc chẵn

D. Đỉnh đầu bậc chẵn đỉnh cuối bậc lẻ

Xem đáp án

Câu 338:

Nếu G là đồ thị Euler thì:

A. Không có đỉnh bậc chẵn

B. Không có đường đi Euler.

C. Không có chu trình Euler

D. Có chu trình Euler

Xem đáp án

Câu 339:

Số màu của đồ thị C_n (với n chẵn) là:

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Câu 340:

Số màu của đồ thị Cn (với n lẻ) là:

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Câu 341:

Chu trình Hamilton là:

A. Chu trình đi qua tất cả các đỉnh mỗi đỉnh đúng một lần trừ đỉnh bậc lẻ

B. Chu trình đi qua tất cả các đỉnh mỗi đỉnh đúng một lần trừ đỉnh bậc chẵn

C. Chu trình đi qua tất cả các đỉnh của đồ thị mỗi đỉnh đúng một lần

D. Chu trình đi qua tất cả các đỉnh của đồ thị mỗi đỉnh hơn một lần

Xem đáp án

Câu 342:

Đồ thị liên thông G có một đỉnh có bậc bằng một thì:

A. G có chu trình Hamilton

B. G có chu trình Euler

C. G không có chu trình Hamilton

D. G không có chu trình

Xem đáp án

Câu 343:

Khi xây dựng chu trình Hamilton, nếu lấy hai cạnh liên thuộc với một đỉnh đặt vào chu trình thì:

A. Có thể xóa tất cả các cạnh còn lại không liên thuộc với đỉnh đó.

B. Có thể xóa tất cả các cạnh còn lại liên thuộc với đỉnh đó.

C. Có thể xóa tất cả các cạnh còn lại của đồ thị.

D. Có thể lấy thêm các cạnh liên thuộc với đỉnh đó.

Xem đáp án

Câu 344:

Số màu trong đồ thị hình bánh xe Wn (với n chẵn) là:

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Câu 345:

Số màu trong đồ thị hình bánh xe Wn (với n lẻ) là:

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Câu 346:

Cho đơn đồ thị phẳng liên thông có số đỉnh bằng 6 và mỗi đỉnh đều bậc 4. Số miền trong biểu diễn phẳng của đồ thị là:

A. 5 miền

B. 6 miền

C. 7 miền

D. 8 miền

Xem đáp án

Câu 347:

Đồ thị nào trong các đồ thị không phẳng sau đây có tính chất: bỏ đi một đỉnh bất kỳ và các cạnh liên thuộc với nó tạo ra một đồ thị phẳng.

A. K5

B. K2

C. K6

D. K7

Xem đáp án

Câu 348:

Độ phức tạp của thật toán Floyd là:

A. O(n3 log2n)

B. O(n2)

C. O(n3)

D. O(n2 log2n)

Xem đáp án

Câu 349:

Thuật toán Dijkstra được áp dụng cho:

A. Đồ thị vô hướng hoặc có hướng có trọng số không âm.

B. Đồ thị liên thông có trọng số không âm

C. Đồ thị có hướng có trọng số không âm.

D. Đồ thị vô hướng hoặc có hướng không có chu trình âm

Xem đáp án

Câu 350:

Thuật toán Dijkstra được dùng để:

A. Tìm đường đi ngắn nhất giữa các cặp đỉnh bất kì của đồ thị.

B. Tìm đường đi ngắn nhất từ một đỉnh đến các đỉnh còn lại của đồ thị

C. Tìm đường đi ngắn nhất giữa hai đỉnh của đồ thị.

D. Tìm đường đi ngắn nhất giữa một đỉnh nguồn và một đỉnh đích.

Xem đáp án

Câu 351:

Với đồ thị n đỉnh, độ phức tạp tính toán của thuật toán Dijkstra là:

A. O(n3 log2n)

B. O(n3)

C. O(n2)

D. O(n2 log2n)

Xem đáp án

Câu 352:

Thuật toán Floy được dùng để:

A. Tìm đường đi ngắn nhất giữa mọi cặp đỉnh của đồ thị.

B. Tìm đường đi ngắn nhất từ một đỉnh đến các đỉnh còn lại của đồ thị.

C. Tìm đường đi ngắn nhất giữa hai cặp đỉnh của đồ thị.

D. Tìm đường đi ngắn nhất giữa một đỉnh nguồn và một đỉnh đích

Xem đáp án

Câu 353:

Số cạnh của cây với 1000 đỉnh là:

A. 9900

B. 9999

C. 10000

D. 1001

Xem đáp án

Câu 354:

Để xây dựng cây khung nhỏ nhất của đồ thị, ta dùng:

A. Tìm kiếm theo chiều sâu (DFS).

B. Thuật toán Floyd.

C. Thuật toán Prim.

D. Thuật toán Dijsktra.

Xem đáp án

Câu 355:

Để xây dựng cây khung nhỏ nhất của đồ thị, ta dùng: (Chọn phương án đúng)

A. Thuật toán Dijsktra.

B. Tìm kiếm theo chiều rộng (BFS).

C. Tìm kiếm theo chiều sâu (DFS).

D. Thuật toán Prim.

Xem đáp án

Câu 356:

Thuật toán Kruskal áp dụng cho đồ thì G, n đỉnh sẽ dừng khi:

A. Kết nạp được n-1 cạnh vào cây khung.

B. Kết nạp được n cạnh vào cây khung.

C. Kết nạp được n – 2 cạnh vào cây khung.

D. Kết nạp được n - 3 cạnh vào cây khung.

Xem đáp án

Câu 357:

Sự giống nhau giữa thuật toán Prim và thuật toán Kruskal là:

A. Dừng khi kết nạp được tất cả các cạnh vào cây khung.

B. Dừng khi kết nạp được n đỉnh và n cạnh vào cây khung

C. Thuật toán chọn các cạnh có trọng số tối thiểu, liên thuộc với các đỉnh đã thuộc cây khung và không tạo ra chu trình.

D. Thuật toán xây dựng cây khung ngắn nhất.

Xem đáp án

Câu 358:

Sự khác nhau giữa thuật toán Prim và thuật toán Kruskal:

A. Thuật toán Prim chọn các cạnh có trọng số tối thiểu, liên thuộc trong khi thuật toán Kruskal chọn các cạnh có trọng số tối thiểu, mà không nhất thiết phải liên thuộc.

B. Thuật toán Prim chọn các cạnh có trọng số tối thiểu, liên thuộc với một đỉnh thuộc cây khung và không tạo thành chu trình. Thuật toán Kruskal chọn các cạnh có trọng số tối thiểu, mà không nhất thiết phải liên thuộc với các đỉnh đã thuộc cây khung và không tạo thành chu trình.

C. Thuật toán Prim chọn các cạnh có trọng số tối thiểu, mà không nhất thiết phải liên thuộc với các đỉnh đã thuộc cây và không tạo thành chu trình. Thuật toán Kruskal chọn các cạnh có trọng số tối thiểu, liên thuộc với các đỉnh đã thuộc cây và không tạo thành chu trình.

D. Thuật toán Prim chọn các cạnh có trọng số tối thiểu, không liên thuộc với một đỉnh thuộc cây khung và không tạo thành chu trình. Thuật toán Kruskal chọn các cạnh có trọng số tối thiểu, mà không nhất thiết phải liên thuộc với các đỉnh đã thuộc cây khung và không tạo thành chu trình.

Xem đáp án

Câu 359:

Trong thuật toán Ford – Fullkerson giải bài toán luồng cực đại, bước tăng luồng thực hiện trên.

A. Các cạnh nằm ngoài đường đi đánh dấu.

B. Các cạnh nằm trên đường đi đánh dấu

C. Trên cạnh nối đỉnh phát với đỉnh thu.

D. Trên đỉnh phát và đỉnh thu.

Xem đáp án

Câu 360:

Trong thuật toán Ford – Fullkerson tìm luồng cực đại, thực hiện lặp đi lặp lại thao tác:

A. Đánh dấu các đỉnh và cải tiến luồng.

B. Nâng giá trị luồng.

C. Giảm giá trị luồng.

D. Giảm khả năng thông qua của các cạnh.

Xem đáp án

Câu 361:

Giá trị của luồng cực đại trong mạng:

A. Lớn hơn khả năng thông qua của mọi lát cắt.

B. Bằng khả năng thông qua của một lát cắt.

C. Không vượt quá khả năng thông qua của lát cắt hẹp nhất trong mạng.

D. Không vượt quá khả năng thông qua của lát cắt lớn nhất trong mạng.

Xem đáp án

Câu 362:

G là một đơn đồ thị phẳng liên thông n đỉnh, m cạnh, gọi r là số miền trong biểu diễn phẳng của G khi đó:

A. r ≠ m – n + 2 r ≠ m – n + 2

B. r = m – n + 2 r = m – n + 2

C. r ≥ m – n + 2 r ≥ m – n + 2

D. r ≤ m – n + 2 r ≤ m – n + 2

Xem đáp án

Câu 363:

Nếu một đơn đồ thị phẳng liên thông có n đỉnh, m cạnh ( n ≥ 3 ) ( n ≥ 3 ) thì:

A. m ≠ 2 n − 4 m ≠ 2 n − 4

B. m = 2 n − 4 m = 2 n − 4

C. m ≤ 2 n − 4 m ≤ 2 n − 4

D. m ≥ 2 n − 4 m ≥ 2 n − 4

Xem đáp án

Câu 364:

Theo định lý Ford – Fulkerson giá trị luồng cực đại từ điểm phát s đến điểm thu t.

A. Bằng khả năng thông qua của lát cắt hẹp nhất tách điểm s và t.

B. Bằng khả năng thông qua của lát cắt lớn nhất tách điểm s và t.

C. Không vượt quá khả năng thông qua của lát cắt lớn nhất tách điểm s và t.

D. Tất cả các đáp án đều sai

Xem đáp án

Câu 365:

Đồ thị G = (V,E) được gọi là đơn đồ thị nếu.

A. giữa hai đỉnh bất kỳ i , j ∈ V i , j ∈ V , có nhiều nhất một cạnh, có kể đến thứ tự các đỉnh.

B. Giữa hai đỉnh bất kỳ i , j ∈ V i , j ∈ V , có nhiều nhất một cạnh.

C. Giữa hai đỉnh bất kỳ i , j ∈ V i , j ∈ V , có thể có nhiều hơn một cạnh, có kể đến thứ tự các đỉnh.

D. Giữa hai đỉnh bất kỳ i , j ∈ V i , j ∈ V , có thể có nhiều hơn một cạnh, không kể đến thứ tự các đỉnh.

Xem đáp án

Câu 366:

Nếu G = (V,E) là một đơn đồ thị vô hướng thì:

A. G không có khuyên, không có cạnh bội.

B. G không có khuyên, có thể có cạnh bội.

C. G có khuyên, không có cạnh bội.

D. G có khuyên, có thể có cạnh bội.

Xem đáp án

Câu 367:

Đồ thị G = (V,E) được gọi là đồ thị vô hướng nếu:

A. Tồn tại một cạnh của G là cạnh vô hướng

B. Mọi cạnh của G là cạnh vô hướng

C. Có hai cạnh của G là cạnh vô hướng

D. Mọi cạnh của G là cạnh có hướng

Xem đáp án

Câu 368:

Nếu G = (V,E) là một đơn đồ thị vô hướng thì: (Chọn phương án đúng)

A. Ma trận kề gồm các phần tử đối xứng nhau qua đường chéo chính

B. Ma trận kề gồm các phần tử không đối xứng nhau qua đường chéo chính

C. Các phần tử trên đướng chéo chính bằng 1

D. Các phần tử trên đường chéo phụ bằng 1

Xem đáp án

Câu 369:

Nếu G = (V,E) là một đa đồ thị vô hướng thì:

A. G không có khuyên

B. G chứa cạnh bội

C. G không có cạnh bội.

D. G có thể có cạnh có hướng

Xem đáp án

Câu 370:

Ta gọi đỉnh v là đỉnh treo trong đồ thị vô hướng G = (V,E) A).

A. Nếu bậc của đỉnh v là 0.

B. Nếu bậc của đỉnh v là một số lẻ.

C. Nếu bậc của đỉnh v là một số chẵn.

D. Nếu bậc của đỉnh v là 1.

Xem đáp án

Câu 371:

Đồ thị vô hướng G = (V,E) được gọi là liên thông nếu.

A. Giữa hai đỉnh bất kỳ u , v ∈ V u , v ∈ V luôn tồn tại đường đi từ u đến v.

B. Nếu u , v ∈ V u , v ∈ V , thì tồn tại v khác u sao cho v liên thông với u.

C. Nếu u , v ∈ V u , v ∈ V , thì với mọi v khác u đều kề với u.

D. Nếu u , v ∈ V u , v ∈ V , thì tồn tại đỉnh v khác u kề với u.

Xem đáp án

Câu 372:

Đồ thị có hướng G =(V,E) được gọi là liên thông mạnh nếu:

A. Giữa hai đỉnh bất kỳ u , v ∈ V u , v ∈ V luôn tìm được đường đi từ u đến v và đường đi từ v đến u.

B. Giữa hai đỉnh bất kỳ u , v ∈ V u , v ∈ V luôn tìm được đường đi từ u đến v

C. Giữa hai đỉnh bất kỳ u , v ∈ V u , v ∈ V luôn tìm được đường đi từ v đến u

D. Giữa hai đỉnh bất kỳ u , v ∈ V u , v ∈ V không tồn tại đường đi từ u đến v

Xem đáp án

Câu 373:

Ta nói cặp hai đỉnh (u,v) là cạnh vô hướng của đồ thị G = (V,E) nếu:

A. u , v × V u , v × V và u, v có thứ tự

B. u , v × V u , v × V và u, v có thứ tự

C. u , v × V u , v × V và u, v không có thứ tự

D. u , v × V u , v × V và u, v không có thứ tự

Xem đáp án

Câu 374:

Ma trận kề của đồ thị vô hướng G = (V,E) có tính chất:

A. Là ma trận đơn vị.

B. Là ma trận đối xứng.

C. Là ma trận không đối xứng.

D. Là ma trận đường chéo trên.

Xem đáp án

Câu 375:

Ma trận kề của đồ thị có hướng không phải là:

A. Ma trận đối xứng.

B. Ma trận đướng chéo trên.

C. Ma trận không đối xứng.

D. Ma trận đường chéo dưới.

Xem đáp án

Câu 376:

Trong biểu diễn đồ thị bởi danh sách kề, mỗi đỉnh của đồ thị có một danh sách:

A. Các cạnh kề với đỉnh đó

B. Các bậc của đỉnh kề với đỉnh đó

C. Các đỉnh kề với đỉnh đó

D. Các cạnh kề với cạnh đó

Xem đáp án

Câu 377:

Ma trận kề của một đơn đồ thị vô hướng đầy đủ là:

A. Ma trận tam giác trên.

B. Ma trận tam giác dưới

C. Ma trận có các phần tử trên đường chéo chính bằng 0, các phần tử khác bằng 1.

D. Ma trận có các phần tử trên đường chéo chính bằng 1, các phần tử khác bằng 0.

Xem đáp án

Câu 378:

Cho ma trận kề A[n,n] biểu diễn đồ thị G vô hướng, n đỉnh, giá trị A[i,j] của ma trận kề xác định:

A. Có cạnh giữa đinh i và đỉnh j

B. Có cạnh giữa đinh j và đỉnh i

C. Không có cạnh giữa đinh i và đỉnh j

D. Không có cạnh giữa đinh i và đỉnh j

Xem đáp án

Câu 379:

Đường đi trong đồ thị G vô hướng từ đỉnh s đến đỉnh t là một dãy:

A. Các cạnh e1,e2,…,en kề nhau

B. Các đỉnh v0 = s, v1, v2, …,vn = t kề nhau, các cạnh ei=(vi-1,vi) đôi một khác nhau, i = 0..n.

C. Các cạnh e1,e2,…,en không kề nhau.

D. Các đỉnh v0 = s, v1, v2, …,vn = t không kề nhau

Xem đáp án

Câu 380:

Cho đồ thị G vô hướng, đỉnh v × G v × G có bậc bằng 1 khi:

A. Có một cạnh xuất phát từ v

B. Có hơn một cạnh xuất phát từ v

C. Có đúng một cạnh đi vào và có hơn một đỉnh đi ra khỏi đỉnh này.

D. Tồn tại khuyên ở đỉnh đó.

Xem đáp án

Câu 381:

Đồ thị G là không liên thông nếu nó chứa:

A. Cạnh có hướng

B. Đỉnh cô lập

C. Đỉnh treo.

D. Cạnh vô hướng

Xem đáp án

Câu 382:

Đồ thị G vô hướng được gọi là liên thông nếu giữa mọi cặp đỉnh u,v bất kỳ đều có:

A. Một cạnh nối giữa u và v

B. Một đường đi có hướng nối u đến v

C. Một đường đi vô hướng nối u đến v

D. Hai cạnh nối u đến v

Xem đáp án

Câu 383:

Chu trình trên đồ thị G là:

A. Đường đi có hướng với đỉnh đầu và đỉnh cuối trùng nhau.

B. Đường đi có đỉnh đầu và đỉnh cuối trùng nhau.

C. Đường đi có đỉnh đầu và đỉnh cuối kề nhau.

D. Đường đi có đỉnh đầu và đỉnh cuối không kề nhau

Xem đáp án

Câu 384:

Số đỉnh bậc lẻ trong đồ thị G vô hướng:

A. Phụ thuộc vào số đỉnh của đồ thị.

B. Là một số lẻ

C. Là một số chẵn.

D. Phụ thuộc vào số cạnh của đồ thị.

Xem đáp án

Câu 385:

Chu trình đơn trên đồ thị G là:

A. Đường đi đơn có đỉnh đầu và đỉnh cuối trùng nhau.

B. Đường đi có hướng với đỉnh đầu và đỉnh cuối trùng nhau.

C. Đường đi đơn có đỉnh đầu và đỉnh cuối kề nhau.

D. Đường đi có đỉnh đầu và đỉnh cuối khác nhau

Xem đáp án

Câu 386:

Bậc của đỉnh trong đồ thị có hướng G là:

A. Số cạnh đi vào đỉnh đó.

B. Số cạnh đi ra khỏi đỉnh đó.

C. Tổng của cạnh đi vào và số cạnh đi ra khỏi đỉnh đó.

D. Hiệu của cạnh đi vào và cạnh đi ra khỏi đỉnh đó

Xem đáp án

Câu 387:

Độ dài của một chu trình trên đồ thị G là:

A. Số cạnh tạo thành chu trình.

B. Số đỉnh tạo thành chu trình +1.

C. Số cạnh tạo chu trình + 1.

D. Số đỉnh trên tạo chu trình – 1.

Xem đáp án

Câu 388:

Đỉnh cô lập trên đồ thị G là:

A. Đỉnh có 2 đỉnh kề với nó.

B. Đỉnh có bậc bằng 1

C. Đỉnh có bậc bằng 0

D. Đỉnh có bậc -1

Xem đáp án

Câu 389:

Đường đi đơn trong đồ thị G là đường đi:

A. Các đỉnh trên nó đối xứng từng đôi một

B. Các đỉnh chỉ xuất hiện một lần trừ đỉnh đầu và đỉnh cuối.

C. Đỉnh đầu và đỉnh cuối khác nhau.

D. Mỗi đỉnh chỉ kề với hai đỉnh.

Xem đáp án

Câu 390:

Độ dài của một chu trình trên đồ thị G là:

A. Số cạnh tạo thành chu trình.

B. Số đỉnh tạo thành chu trình +1.

C. Số cạnh tạo chu trình + 1.

D. Số đỉnh trên tạo chu trình – 1.

Xem đáp án

Câu 391:

Đỉnh cô lập trên đồ thị G là:

A. Đỉnh có 2 đỉnh kề với nó.

B. Đỉnh có bậc bằng 1

C. Đỉnh có bậc bằng 0

D. Đỉnh có bậc -1

Xem đáp án

Câu 392:

Đường đi đơn trong đồ thị G là đường đi:

A. Các đỉnh trên nó đối xứng từng đôi một

B. Các đỉnh chỉ xuất hiện một lần trừ đỉnh đầu và đỉnh cuối.

C. Đỉnh đầu và đỉnh cuối khác nhau.

D. Mỗi đỉnh chỉ kề với hai đỉnh.

Xem đáp án

Câu 393:

Đồ thị đầy đủ Kn có số đỉnh và số cạnh tương ứng là:

A. n, 2n.

B. n, n(2n-1)/2.

C. n+1, 2n.

D. n, n(n-1)/2.

Xem đáp án

Câu 394:

Đồ thị Cn có số đỉnh và số cạnh tương ứng là:

A. n, n+1

B. n, n

C. n, n-1

D. n, 2n

Xem đáp án

Câu 395:

Đồ thị lập phương Qn là đồ thị:

A. 2n đỉnh, mỗi đỉnh kề nhau chỉ khác nhau một bit.

B. 2n đỉnh, mỗi đỉnh kề nhau chỉ khác nhau nhiều nhất 2 bit.

C. 2n đỉnh, mỗi đỉnh được biểu diễn bởi một xâu bit độ dài n sao cho hai đỉnh kề nhau chỉ khác nhau một bit

D. n đỉnh, mỗi đỉnh được biểu diễn bởi một xâu bit độ dài n sao cho hai đỉnh kề nhau chỉ khác nhau một bit.

Xem đáp án

Câu 396:

Chu trình Euler của đồ thị là chu trình đi qua tất cả các đỉnh.

A. Mỗi đỉnh đúng một lần.

B. Mỗi cạnh đúng một lần.

C. Mỗi cạnh không quá một lần

D. Đi qua đỉnh đầu và đỉnh cuối hai lần

Xem đáp án

Câu 397:

Chu trình Euler đi qua mỗi đỉnh của đồ thị:

A. Không quá một lần

B. Đúng một lần.

C. Không xác định

D. Nhiều hơn một lần

Xem đáp án

Câu 398:

Đường đi Euler đi qua mỗi cạnh của đồ thị:

A. Không quá một lần.

B. Đúng một lần.

C. Không xác định

D. Có thể nhiều hơn một lần.

Xem đáp án

Câu 399:

Chu trình Hamilton là chu trình đi qua tất cả các đỉnh của đồ thị mỗi đỉnh.

A. Không quá một lần.

B. Đúng một lần.

C. Luôn nhiều hơn một lần.

D. Không xác định

Xem đáp án

Câu 400:

Đường đi Hamilton là đường đi đi qua tất cả các đỉnh của đồ thị mỗi đỉnh.

A. Đúng một lần

B. Luôn nhiều hơn một lần.

C. Không quá một lần.

D. Không xác định.

Xem đáp án

Câu 401:

Đồ thị G được gọi là nửa Hamilton nếu tồn tại đường đi đi qua tất cả các đỉnh của đồ thị.

A. Mỗi cạnh một lần.

B. Mỗi cạnh không quá một lần.

C. Mỗi đỉnh một lần.

D. Một đỉnh không quá một lần.

Xem đáp án

Câu 402:

Đa đồ thị liên thông G có chu trình Hamilton nếu:

A. Bậc của các đỉnh trong đồ thị -2

B. Bậc của các đỉnh trong đồ thị -n

C. Bậc của các đỉnh trong đồ thị -n/2

D. Bậc của các đỉnh trong đồ thị -n/4

Xem đáp án

Câu 403:

Một đồ thị được gọi là phẳng nếu:

A. Có thể vẽ được trên một mặt phẳng mà có các cạnh cắt nhau ở đỉnh ngoài

B. Có thể vẽ được trên một mặt phẳng mà không có các cạnh nào cắt nhau

C. Có thể vẽ được trên một mặt phẳng mà có hai cạnh bất kỳ cắt nhau

D. Có thể vẽ được trên một mặt phẳng mà không có quá hai cạnh cắt nhau

Xem đáp án

Câu 404:

Số màu của một đồ thị là:

A. Số trung bình các màu cần thiết để tô màu đồ thị này

B. Số tối thiểu các màu cần thiết để tô màu đồ thị này

C. Số tối đa các màu cần thiết để tô màu đồ thị này

D. Số theo yêu cầu các màu cần thiết để tô màu đồ thị này

Xem đáp án

Câu 405:

Số màu của một đồ thị phẳng là:

A. Bằng 5.

B. Lớn hơn 4.

C. Lớn hơn hoặc bằng 5.

D. Không lớn hơn 4

Xem đáp án

Câu 406:

Đồ thị đầy đủ Kn có số màu bằng:

A. (n- 2)

B. n

C. (n-1)

D. n(n-1)/2

Xem đáp án

Câu 407:

Đồ thị G vô hướng n đỉnh là một cây nếu:

A. Nếu liên thông và có n-1 cạnh

B. Nếu không liên thông và có n-1 cạnh

C. Nếu liên thông và có n cạnh

D. Nếu không liên thông và có n cạnh

Xem đáp án

Câu 408:

Cây là một đồ thị vô hướng:

A. Liên thông và số đỉnh nhỏ hơn số cạnh là 1.

B. Liên thông và số đỉnh bằng số cạnh

C. Liên thông và không chứa chu trình

D. Không liên thông và có số đỉnh bằng số cạnh là 1.

Xem đáp án

Câu 409:

Bài toàn xây dựng cây khung nhỏ nhất của đồ thị được phát biểu trên:

A. Đồ thị có hướng có trọng số

B. Đồ thị vô hướng có trọng số bất kỳ

C. Đồ thị vô hướng

D. Đồ thị vô hướng có trọng số dương

Xem đáp án

Câu 410:

Cho G =(V,E) là đồ thị vô hướng liên thông n đỉnh. T = (V_T, E_T) được gọi là cây khung của đồ thị G nếu:

A. T liên thông và chứa n đỉnh của G.

B. T không liên thông, không chứa chu trình và chứa n cạnh của G.

C. T liên thông, không chứa chu trình và chứa n đỉnh của G.

Xem đáp án

Câu 411:

Cây là đồ thị vô hướng liên thông:

A. Không có chu trình.

B. Không có đỉnh cô lập

C. Không có cạnh cầu

D. Không có đỉnh treo

Xem đáp án

Câu 412:

Cho mạng G, điểm phát s điểm thu t. Tính cân bằng của luồng f trên mạng G phải thỏa mãn cho:

A. Tất cả các đỉnh của G.

B. Tất cả các đỉnh của G trừ đỉnh phát s.

C. Tất cả các đỉnh của G rừ đỉnh thu t.

D. Tất cả các đỉnh của G trừ đỉnh phát s và đỉnh thu t.

Xem đáp án

Câu 413:

Cho mạng G, điểm phát s điểm thu t. Lát cắt (X, Y) trong đó X + V, Y= V - X là:

A. Tập hợp tất cả các cung (vi , vj) sao cho hoặc vi x X, vj x Y và vj x X, vi x Y

B. Tập hợp tất cả các cung (vi, vj) sao cho hoặc vi x X, vj x Y hoặc vj x X, vi x Y

C. Tập hợp tất cả các cung (vi , vj) sao cho hoặc vi x X, vj x X hoặc vj x X, vi x Y

D. Tập hợp tất cả các cung (vi , vj) sao cho hoặc vi x X, vj x Y hoặc vj x Y, vi x Y

Xem đáp án

Câu 414:

Cho mạng G, điểm phát s điểm thu t. Lát cắt (X, Y) được gọi là lát cắt hẹp nhất nếu:

A. khả năng thông qua của lát cắt (X,Y) bằng tổng khả năng thông qua của các cung đi ra khỏi đỉnh s

B. khả năng thông qua của lát cắt (X,Y) bằng tổng khả năng thông qua của các cung đi vào đỉnh t

C. khả năng thông qua của lát cắt (X,Y) lớn nhất.

D. khả năng thông qua của lát cắt (X,Y) bé nhất.

Xem đáp án

Câu 415:

Cho đồ thị G = (V,E) vô hướng. Bậc của các đỉnh 1, 2, 3, 4, 5 tương ứng là:

A. 3, 3, 4, 6, 4

B. 3, 4, 6, 4, 4

C. 3, 4, 6, 4, 5

D. 3, 4, 5, 4, 4

Xem đáp án

Câu 416:

Có bao nhiêu cạnh trong đồ thị có 10 đỉnh, mỗi đỉnh có bậc bằng 6?

A. 60

B. 45

C. 30

D. 20

Xem đáp án

Câu 417:

Đồ thị G vô hướng nào trong các đồ thị sau là tồn tại nếu các đỉnh có số bậc lần lượt là:

A. 2, 4, 3, 1, 4, 2, 5

B. 3, 4, 2, 1, 4, 2, 6

C. 5, 2, 2, 1, 3, 2, 4

D. 2, 1, 4, 3, 4, 2, 7

Xem đáp án

Câu 418:

Cho đồ thị như hình vẽ. Kết quả khi duyệt đồ thị theo thuật toán BFS(I) là:

A. I, A, E, G, K, B, C, F, H, D

B. I, A, E, G, C, K, B, F, H, D

C. I, A, B, C, D, E, G, H, F, K

D. I, A, B, D, E, G, C, F, H, K

Xem đáp án

Câu 419:

Cho đồ thị như hình vẽ. Kết quả khi duyệt đồ thị theo thuật toán BFS(K) là:

A. K, A, B, C, D, E, F, G, H, I

B. K, A, C, E, G, B, D, F, H, I

C. K, I, E, G, F, H, A, B, C, D

D. K, I, A, E, G, B, C, F, H, D

Xem đáp án

Câu 420:

Cho đồ thị như hình vẽ. Kết quả khi duyệt đồ thị theo thuật toán BFS(I) là:

A. I, A, C, H, E, G, B, D, F, K

B. I, A, B, C, D, E, G, F, H, K

C. I, A, C, K, E, G, B, D, F, H

D. I, E, F, G, H, A, B, C, D, K

Xem đáp án

Câu 421:

Cho đồ thị như hình vẽ. Kết quả khi duyệt đồ thị theo thuật toán BFS(H) là:

A. H, G, F, D, E, F, A, B, C, I

B. H, F, G, E, K, I, A, C, B, D

C. H, G, F, B, D, E, K, A, C, I

D. H, E, F, G, H, I, A, B, C, D

Xem đáp án

Câu 422:

Một công thức được gọi là có dạng chuẩn tắc hội nếu …?

A. Nó là hội của các biểu thức hội cơ bản

B. Nó là hội của các biểu thức tuyển cơ bản

C. Nó là tuyển của các biểu thức hội cơ bản

D. Nó là tuyển của các biểu thức tuyển cơ bản

Xem đáp án

Câu 423:

Một công thức được gọi là có dạng chuẩn tắc tuyển nếu …?

A. Nó là hội của các biểu thức hội cơ bản

B. Nó là hội của các biểu thức tuyển cơ bản

C. Nó là tuyển của các biểu thức hội cơ bản

D. Nó là tuyển của các biểu thức tuyển cơ bản

Xem đáp án

Câu 424:

Xác định chân trị của biểu thức ( P → Q ) Λ ( Q → R ) và (P → R) khi P = Q = 1, R=0?

A. 1 và 1

B. 0 và 0

C. 1 và 0

D. 0 và 1

Xem đáp án

Câu 425:

Biết chân trị của mệnh đề P → Q là 0, thì chân trị của các mệnh đề P Λ Q và Q → P tương ứng là?

A. 0 và 1

B. 1 và 0

C. 0 và 0

D. 1 và 1

Xem đáp án

Câu 426:

Mệnh đề P ∨ ( P ∧ Q ) P ∨ ( P ∧ Q ) tương đương logic với mệnh đề nào sau đây?

A. P ∧ Q P ∧ Q

B. Q

C. P ∨ Q P ∨ Q

D. P

Xem đáp án

Câu 427:

Phương pháp phản chứng là phương pháp?

A. Quy bài toán ban đầu về bài toán con đơn giản hơn

B. Giả sử điều cần chứng minh là sai để từ đó suy ra mâu thuẫn

C. Liệt kê tất cả các khả năng để từ đó đưa ra quyết định.

D. Biểu diễn nghiệm của bài toán bằng các dữ kiện ban đầu

Xem đáp án

Câu 428:

Quy tắc suy luận nào sau đây là quy tắc tam đoạn luận?

A. ( P ∧ ( P → Q ) ) → Q ( P ∧ ( P → Q ) ) → Q

B. ( ( P → Q ) ∨ ( Q → R ) ) → ( P → R ) ( ( P → Q ) ∨ ( Q → R ) ) → ( P → R )

C. ( ( P → Q ) ∨ ( Q → R ) ) → ( Q → R ) ( ( P → Q ) ∨ ( Q → R ) ) → ( Q → R )

D. ( ( P → Q ) ∧ ( Q → R ) ) → ( P → R ) ( ( P → Q ) ∧ ( Q → R ) ) → ( P → R )

Xem đáp án

Câu 429:

Qui tắc suy luận nào là cơ sở của suy diễn sau: "Nếu hôm nay trời mưa thì cô ta không đến, Nếu cô ta không đến thì ngày mai cô ta đến, Vậy thì, nếu hôm nay trời mưa thì ngày mai cô ta đến."

A. Modus Ponens (Khẳng định)

B. Modus Tollens (Phủ định)

C. Tam đoạn luận (Bắc cầu)

D. Từng trường hợp

Xem đáp án

Câu 430:

Có bao nhiêu trường hợp về chân trị của bộ biến mệnh đề (q1,q2,..,qn)?

A. 2n

B. 2n

C. 2n+1

D. 2n-1

Xem đáp án

Câu 431:

Bảng chân trị của biểu thức logic E(q1,q2,..,qn) là…?

A. Bảng liệt kê tất cả các giá trị của biểu thức E theo từng trường hợp về chân trị của bộ biến mệnh đề q1,q2,..,qn.

B. Bảng giá trị của biểu thức E

C. Bảng liệt kê các trường hợp của bộ biến mệnh đề q1,q2,..,qn

D. Bảng liệt kê các phép toán logic theo các trường hợp về chân trị của bộ biến mệnh đề.

Xem đáp án

Câu 432:

Quy tắc (luật )suy luận nào là cơ sở của suy diễn sau: Là phi công thì phải biết lái máy bay. An là phi công nên An biết lái máy bay

A. Luật cộng

B. Luật rút gọn

C. Luật khẳng định

D. Luât phủ định

Xem đáp án

Câu 433:

Quy tắc (luật )suy luận nào là cơ sở của suy diễn sau: Nếu là sinh viên CNTT của trường DHCN Việt Hung thì phải học Toán rời rạc. An không học Toán rời rạc nên An không phải là sinh viên CNTT của trường ĐHCN Việt Hung.

A. Luật khẳng định

B. Luật phủ định

C. Luật tam đoạn luận

D. Luật tam đoạn luận rời

Xem đáp án

Câu 434:

Quy tắc (luật )suy luận nào là cơ sở của suy diễn sau: Trường chất lượng cao thì có cán bộ giảng dạy giỏi. Trường có cán bộ giảng dạy giỏi thì có sinh viên giỏi. Vậy trường chất lượng cao thì có sinh viên giỏi.

A. Luật khẳng định

B. Luật phủ định

C. Luật tam đoạn luận

D. Luật tam đoạn luận rời

Xem đáp án

Câu 435:

Quy tắc (luật )suy luận nào là cơ sở của suy diễn sau: Được khen thưởng nếu học giỏi hoặc công tác tốt. An được khen thưởng, nhưng An không học giỏi nên An phải công tác tốt.

A. Luật khẳng định

B. Luật phủ định

C. Luật tam đoạn luận

D. Luật tam đoạn luận rời

Xem đáp án

Câu 436:

Quy tắc (luật )suy luận nào là cơ sở của suy diễn sau : Nếu An học giỏi thì An sẽ được khen thưởng. Và nếu An nhiệt tình tham gia các hoạt động Đoàn thì An cũng được khen thưởng. Vậy Nếu An học giỏi hoặc tham gia nhiệt tình các hoạt động Đoàn thì An sẽ được khen thưởng.

A. Luật khẳng định

B. Luật phủ định

C. Luật tam đoạn luận

D. Luật từng trường hợp

Xem đáp án

Câu 437:

Quy tắc (luật )suy luận nào là cơ sở của suy diễn sau : Nếu An học giỏi thì An sẽ tốt nghiệp loại A. Và nếu An tốt nghiệp loại A thì An sẽ có nhiều cơ hội tìm việc làm khi ra trường. Vậy nếu An học giỏi thì An sẽ có nhiều cơ hội tìm việc làm khi ra trường.

A. Luật khẳng định

B. Luật phủ định

C. Luật tam đoạn luận

D. Luật từng trường hợp

Xem đáp án

Câu 438:

Xác định chân trị của biểu thức ( ¬ ¬ X→Y ) ∨ ∨ ( ¬ ¬ Y → Z ) và (X →Z) khi X =Y=Z=0?

A. 1 và 1

B. 0 và 0

C. 1 và 0

D. 0 và 1

Xem đáp án

Câu 439:

Xác định chân trị của biểu thức ( X→Y ) ∨ ∨ ( Y → Z ) và (X →Z) khi X = Y=Z=0?

A. 1 và 1

B. 0 và 0

C. 1 và 0

D. 0 và 1

Xem đáp án

Câu 440:

Xác định chân trị của biểu thức ( ¬ ¬ X→Y ) ∨ ∨ ( ¬ ¬ Y → Z ) và ( ¬ ¬ X →Z) khi X = Y=Z=1?

A. 1 và 1

B. 0 và 0

C. 1 và 0

D. 0 và 1

Xem đáp án

Câu 441:

Xác định chân trị của biểu thức ( ¬ ¬ X→ ¬ ¬ Y ) v ( ¬ ¬ Y → ¬ ¬ Z ) và ( ¬ ¬ X → ¬ ¬ Z) khi X = Y=0, Z= 1?

A. 1 và 1

B. 0 và 0

C. 1 và 0

D. 0 và 1

Xem đáp án

Câu 442:

Xác định chân trị của biểu thức ( ¬ ¬ X→ ¬ ¬ Y) ∧ ∧ ( ¬ ¬ Y → ¬ ¬ Z) và ( ¬ ¬ X → ¬ ¬ Z) khi X = Y=0, Z= 1?

A. 1 và 1

B. 0 và 0

C. 1 và 0

D. 0 và 1

Xem đáp án

Câu 443:

Xác định chân trị của biểu thức ( ¬ ¬ X→Y ) ∧ ∧ ( ¬ ¬ Y → Z ) và ( ¬ ¬ X →Z) khi X = Y=0, Z= 1?

A. 1 và 1

B. 0 và 0

C. 1 và 0

D. 0 và 1

Xem đáp án

Câu 444:

Câu nào sau đây KHÔNG là một mệnh đề:

A. Hôm nay không phải Thứ hai

B. Lan học giỏi Tin học

C. Không phải Hiếu được khen thưởng

D. Thật vui vì Lan ở nhà.

Xem đáp án

Câu 445:

Câu nào sau đây KHÔNG phải là một mệnh đề:

A. Có ai ở nhà không?

B. Hà Nội là thủ đô của Việt Nam

C. Hôm nay trời mưa

D. 2+1=5

Xem đáp án

Câu 446:

Câu nào dưới đây KHÔNG là một mệnh đề:

A. An là sinh viên khoa CNTT

B. An không phải học Trí tuệ nhân tạo

C. X là sinh viên không phải học Trí tuệ nhân tạo

D. An là sinh viên CNTT nhưng không phải học Trí tuệ nhân tạo.

Xem đáp án

Câu 447:

Câu nào sau đây là một mệnh đề:

A. Hãy cẩn thận!

B. X+Y=1

C. An hôm nay có phải đi học không?

D. An là học sinh giỏi

Xem đáp án

Câu 448:

Cho X là 1 biến Boole. Xác định biểu thức sai trong các biểu thức sau?

A. X.0=0

B. X.1=1

C. X+0=X

D. X+1=1

Xem đáp án

Câu 449:

Cho X là 1 biến Boole. Xác định biểu thức sai trong các biểu thức?

A. X+0=X

B. X+1=X

C. X + (Y + Z) = (X + Y) + Z = X + Y + Z

D. (W + X)(Y + Z) = WY + XY + WZ + XZ

Xem đáp án

Câu 450:

Hàm Boole f = x + xy tương đương với hàm nào sau đây?

A. f = xy

B. f = y

C. f = x+y

D. f = x

Xem đáp án

Câu 451:

Đại số Boole là…?

A. Một tập hợp với 2 phép toán cộng (+) và nhân (.)

B. Một tập hợp với các phép toán cộng (+) và nhân (.) và lấy phần bù.

C. Một tập hợp với các phép toán cộng (+) và nhân (.) và lấy phần bù; các phép cộng, nhân thoả các tính chất giao hoán, kết hợp, phân bố và có phần tử trung hoà.

D. Một tập hợp với các phép toán cộng (+) và nhân (.); các phép cộng, nhân thoả các tính chất giao hoán, kết hợp, phân bố và có phần tử trung hoà.

Xem đáp án

Câu 452:

Công thức đa thức là?

A. Công thức biểu diễn hàm Boole thành tích của các tích cơ bản (từ tối tiểu)

B. Công thức biểu diễn hàm Boole thành tổng của các tích cơ bản (từ tối tiểu)

C. Công thức biểu diễn hàm Boole thành tổng của các từ đơn

D. Công thức biểu diễn hàm Boole thành tổng của các đơn thức

Xem đáp án

Câu 453:

Dạng chính tắc tuyển (nối rời chính tắc) của hàm Boole là…?

A. Công thức biểu diễn hàm Boole thành tổng của các tích cơ bản (từ tối tiểu)

B. Công thức biểu diễn hàm Boole thành tích của các tích cơ bản (từ tối tiểu)

C. Công thức biểu diễn hàm Boole thành tổng của các đơn thức

Xem đáp án

Câu 454:

Trong bảng Karnaugh, 2 ô gọi là kề nhau nếu...?

A. Chúng nằm trên cùng 1 hàng

B. Chúng nằm trên cùng 1 cột

C. Nếu chúng cùng nằm trên 1 hàng, 1 cột hoặc chúng là ô đầu, ô cuối của cùng một hàng hoặc 1 cột nào đó

D. Nếu chúng là hai ô liền nhau hoặc chúng là ô đầu và ô cuối của cùng một hàng hoặc 1 cột nào đó

Xem đáp án

Câu 455:

Cho đồ thị vô hướng G=(V,E), với |V| = n; |E|=m. Tổng bậc của tất cả các đỉnh trong đồ thị G là?

A. -1.m

B. -2.m

C. 1.m

D. 2.m

Xem đáp án

Câu 456:

Phát biểu nào dưới đây là đúng:

A. Đồ thị G là đơn đồ thị khi và chỉ khi G không có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.

B. Đồ thị G là đơn đồ thị khi và chỉ khi G có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.

C. Đồ thị G là đơn đồ thị khi và chỉ khi G không có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh.

D. Đồ thị G là đơn đồ thị khi và chỉ khi G có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh.

Xem đáp án

Câu 457:

Chọn phát biểu nào sau đây là đúng:

A. Đồ thị G là đa đồ thị khi và chỉ khi G không có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.

B. Đồ thị G là đa đồ thị khi và chỉ khi G có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.

C. Đồ thị G là đa đồ thị khi và chỉ khi G không có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh.

D. Đồ thị G là đa đồ thị khi và chỉ khi G có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh

Xem đáp án

Câu 458:

Phương án nào sau đây là đúng:

A. Đồ thị G là giả đồ thị khi và chỉ khi G không có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.

B. Đồ thị G là giả đồ thị khi và chỉ khi G có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.

C. Đồ thị G là giả đồ thị khi và chỉ khi G không có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh.

D. Đồ thị G là giả đồ thị khi và chỉ khi G có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh

Xem đáp án

Câu 459:

Cho G là đồ thị có hướng, phát biểu nào sau đây là chính xác nhất:

A. G là đơn đồ thị có hướng khi và chỉ khi trong G đối với mỗi cặp đỉnh khác nhau có không quá một cung (cùng chiều) nối với nhau và có thể có khuyên.

B. G là đơn đồ thị có hướng khi và chỉ khi trong G đối với mỗi cặp đỉnh khác nhau có không quá một cung nối với nhau và không có khuyên.

C. G là đơn đồ thị có hướng khi và chỉ khi trong G có một cặp đỉnh khác nhau được nối với nhau bởi nhiều hơn một cung (cùng chiều) và không có khuyên.

D. G là đơn đồ thị có hướng khi và chỉ khi trong G có một cặp đỉnh khác nhau được nối với nhau bởi nhiều hơn một cung (cùng chiều) và có thể có khuyên

Xem đáp án

Câu 460:

Cho G là đồ thị có hướng, phát biểu nào sau đây là đúng nhất:

A. G là đa đồ thị có hướng khi và chỉ khi trong G đối với mỗi cặp đỉnh khác nhau có không quá một cung (cùng chiều) nối với nhau và có thể có khuyên.

B. G là đa đồ thị có hướng khi và chỉ khi trong G đối với mỗi cặp đỉnh khác nhau có không quá một cung nối với nhau và không có khuyên.

C. G là đa đồ thị có hướng khi và chỉ khi trong G có tồn tại một cặp đỉnh khác nhau được nối với nhau bởi nhiều hơn một cung (cùng chiều) và không có khuyên.

D. G là đa đồ thị có hướng khi và chỉ khi trong G có tồn tại một cặp đỉnh khác nhau được nối với nhau bởi nhiều hơn một cung (cùng chiều) và có thể có khuyên

Xem đáp án

Câu 461:

Giả sử G=(V,E) là đồ thị vô hướng. Đỉnh x gọi là đỉnh cô lập nếu?

A. x có bậc 0

B. x có bậc 1

C. x có bậc 2

D. x có bậc 3

Xem đáp án

Câu 462:

Một đơn đồ thị vô hướng liên thông có 6 đỉnh, các đỉnh có bậc lần lượt là 2, 3, 3, 4, 2, 2. Tìm số cạnh của đồ thị?

A. 4

B. 6

C. 8

D. 10

Xem đáp án

Câu 463:

Có bao nhiêu cạnh trong đồ thị có 10 đỉnh, mỗi đỉnh có bậc là 6?

A. 0

B. 10

C. 20

D. 30

Xem đáp án

Câu 464:

Có bao nhiêu cạnh trong đồ thị có 10 đỉnh, mỗi đỉnh có bậc là 4?

A. 0

B. 10

C. 20

D. 30

Xem đáp án

Câu 465:

Phát biểu nào dưới đây là đúng:

A. Đồ thị G là đơn đồ thị khi và chỉ khi G có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.

B. Đồ thị G là đơn đồ thị khi và chỉ khi G không có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.

C. Đồ thị G là đơn đồ thị khi và chỉ khi G không có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh.

D. Đồ thị G là đơn đồ thị khi và chỉ khi G có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh.

Xem đáp án

Câu 466:

Có bao nhiêu cạnh trong đồ thị có 8 đỉnh, mỗi đỉnh có bậc là 10?

A. 10

B. 20

C. 30

D. 40

Xem đáp án

Câu 467:

Cho biết bậc của đồ thị G có n đỉnh, m cạnh?

A. 2.m

B. -2.m

C. 0m

D. 1.m

Xem đáp án

Câu 468:

Cho đồ thị G liên thông có 5 đỉnh. Hỏi cây khung của G có mấy cạnh, mấy đỉnh?

A. 5 cạnh, 5 đỉnh

B. 4 cạnh, 5 đỉnh

C. 5 cạnh, 4 đỉnh

D. 4 cạnh, 4 đỉnh

Xem đáp án

Câu 469:

Cho đồ thị G = (V, E), |V| = n đỉnh, |E| = m cạnh. Khi đó đường đi Hamilton trong G có:

A. n đỉnh

B. n+1 đỉnh

C. 1 đỉnh

D. 2 đỉnh

Xem đáp án

Câu 470:

Phát biểu nào dưới đây là chính xác nhất:

A. Cho G là đồ thị bất kỳ. Một đường đơn trong G là đường Euler khi và chỉ khi đường đơn đó đi qua tất cả các cạnh trong G và mỗi cạnh xuất hiện đúng một lần.

B. Cho G là đồ thị bất kỳ. Một đường đơn trong G là đường Euler khi và chỉ khi đường đơn đó đi qua tất cả các đỉnh trong G và mỗi đỉnh xuất hiện đúng một lần.

C. Cho G là đồ thị bất kỳ. Một đường đi trong G là đường Euler khi và chỉ khi đường đơn đó đi qua các cạnh trong G.

D. Cho G là đồ thị bất kỳ. Một đường đơn trong G là đường Euler khi và chỉ khi đường đơn đó đi qua tất cả các đỉnh trong G.

Xem đáp án

Câu 471:

Chọn phát biểu nào sau đây là chính xác nhất:

A. Cho G là đồ thị bất kỳ. Một đường đi trong G là đường Hamilton khi và chỉ khi đường đi đó đi qua tất cả các cạnh trong G và mỗi cạnh xuất hiện đúng một lần.

B. Cho G là đồ thị bất kỳ. Một đường sơ cấp trong G là đường Hamilton khi và chỉ khi đường đi đó đi qua tất cả các đỉnh trong G và mỗi đỉnh xuất hiện đúng một lần.

C. Cho G là đồ thị bất kỳ. Một đường sơ cấp trong G là đường Hamilton khi và chỉ khi đường đi đó đi qua tất cả các cạnh trong G.

D. Cho G là đồ thị bất kỳ. Một đường đi trong G là đường Hamilton khi và chỉ khi 69 đường đi đó đi qua tất cả các đỉnh trong G.

Xem đáp án

Câu 472:

Cho đồ thị G có bậc là 10. Số cạnh của đồ thị G là:

A. 2

B. 3

C. 4

D. 5

Xem đáp án

Câu 473:

Cho đồ thị G có 9 đỉnh có bậc lần lượt là 1, 2, 2, 3, 3, 4, 4, 4, 5. Số cạnh của đồ thị G là:

A. 8

B. 9

C. 10

D. 14

Xem đáp án

Câu 474:

Một cây có ít nhất mấy đỉnh treo?

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Câu 475:

Cho đồ thị G có 5 đỉnh có bậc lần lượt là 2, 2, 3, 4, 5. Bậc của đồ thị G là:

A. 15

B. 16

C. 17

D. 18

Xem đáp án

Câu 476:

Phương trình x + y + z = 15 có số nghiệm nguyên không âm là:

A. 136

B. 455

C. 15

D. 30

Xem đáp án

Câu 477:

Câu nào sau đây KHÔNG là một mệnh đề?

A. Hôm nay không phải thứ hai.

B. x là bạn cùng lớp với Lan.

C. Nếu hôm nay trời nắng thì tôi sẽ đi chơi.

D. Có một người trong lớp không biết môn toán Rời rạc.

Xem đáp án

Câu 478:

Cho quan hệ R = {(a,b) | a|b}trên tập số nguyên dương. Hỏi R KHÔNG có tính chất nào?

A. Phản xạ

B. Đối xứng

C. Bắc cầu

D. Phản đối xứng

Xem đáp án

Câu 479:

Số xâu khác nhau có thể tạo được từ các chữ cái của từ ORONO là:

A. 10

B. 20 (=C(5,3).C(2,1).C(1,1))

C. 5

D. 100

Xem đáp án

Câu 480:

Trong các phát biểu sau đây phát biểu nào không là mệnh đề.

A. Lan thích học toán.

B. Lan không thích học toán

C. Không ai thích học toán.

D. Mọi người trong lớp tôi đều thích học toán.

Xem đáp án

480 câu Trắc nghiệm tổng hợp Toán rời rạc có đáp án

Đề thi liên quan:

220 câu trắc nghiệm Cấu trúc dữ liệu và giải thuật có đáp án

400 câu Trắc nghiệm tổng hợp Cấu trúc dữ liệu và giải thuật có đáp án

225 câu trắc nghiệm Lập trình hướng đối tượng có đáp án

300 câu trắc nghiệm Vi xử lí có đáp án

200 câu trắc nghiệm Đồ họa máy tính có đáp án

230 câu trắc nghiệm môn Công nghệ phần mềm có đáp án

350 câu Trắc nghiệm tổng hợp Công nghệ phần mềm có đáp án

630 câu hỏi trắc nghiệm môn Mạng máy tính có đáp án

350 Câu hỏi trắc nghiệm môn Lập trình mạng có đáp án

250 Câu hỏi trắc nghiệm Javascript, CSS, HTML có đáp án

Danh sách câu hỏi:

Cho 2 tập A, B rời nhau với | A | = 12 , | B | = 18 , | A ∪ B | | A | = 12 , | B | = 18 , | A ∪ B | là:

Cho tập A={1,2,3,4,5,6,7,8,9}, tập B={1,2,3,9,10}. Tập A - B là:

Cho 2 tập A, B với | A | = 13 , | B | = 19 , | A ∩ B | = 1. | A ∪ B | | A | = 13 , | B | = 19 , | A ∩ B | = 1. | A ∪ B | là:

Cho 2 tập A, B với | A | = 15 , | B | = 20 , A ⊆ B . | A ∪ B | | A | = 15 , | B | = 20 , A ⊆ B . | A ∪ B | là:

Cho biết số phần tử của tập A ∪ B ∪ C A ∪ B ∪ C nếu mỗi tập có 100 phần tử và các tập hợp đôi một rời nhau:

Cho biết số phần tử của A ∪ B ∪ C A ∪ B ∪ C nếu mỗi tập có 100 phần tử và nếu có 50 phần tử chung của mỗi cặp 2 tập và có 10 phần tử chung của cả 3 tập.

Cho X={1,2,3,4,5,6,7,8,9} A={1,2,3,8}, B={2,4,8,9}, C={6,7,8,9} Tìm xâu bit biểu diễn tập: ( A ∪ B ) ∩ C ( A ∪ B ) ∩ C

Cho X={1,2,3,4,5,6,7,8,9}, A={1,2,3,8}. Tìm xâu bit biểu diễn tập ¯¯¯¯A

Cho X={1,2,3,4,5,6,7,8,9}. Xâu bit biểu diễn tập A là: 111001011, xâu bit biểu diễn tập B là 010111001 Tìm xâu bit biểu diễn tập A ∪ B A ∪ B

Cho tập A = {1,2,a}. Hỏi tập nào là tập lũy thừa của tập A?

Xét các hàm từ R tới R, hàm nào là khả nghịch:

Xét các hàm từ R tới R, hàm nào là khả nghịch:

Cho quy tắc f: ℝ → ℝ thỏa mãn f(x)=2x2+5. Khi đó f là:

Cho hàm số f(x)=2x và g(x)=4x2+1, với x ∈ ℝ . Khi đó g.f(-2) bằng:

Cho tập A = {2, 3, 4, 5}. Hỏi tập nào KHÔNG bằng tập A?

Cho tập S = {a, b, c} khi đó số phần tử của tập lũy thừa của tập S là:

Cho tập A = {a, b}, B = {0, 1, 2} câu nào dưới đây là SAI:

Cho 2 tập hợp: A = {1,2,3,4,5,a, hoa, xe máy, dog, táo, mận} B = {hoa, 3,4 , táo} Tập nào trong các tập dưới đây là tập con của tập AxB:

Cho 2 tập A={1, 2, 3}, B={a, b, c, 2}. Trong số các tập dưới đây, tập nào là một quan hệ 2 ngôi từ A tới B?

Xác định tập lũy thừa của tập A={ôtô, Lan}

Xác định tích đề các của 2 tập A={1,a} và B={1,b}:

Cho 2 tập C, D với | C | = 28 , | D | = 32 , | C ∩ D | = 4. | C ∪ D | | C | = 28 , | D | = 32 , | C ∩ D | = 4. | C ∪ D | là:

Cho tập A = {1, 2, 3, 4, 5, 6, 7}, tập B = {2, 3, 8, 1, 7, 9}. Tập ( A − B ) ∪ ( B − A ) ( A − B ) ∪ ( B − A ) là:

Cho 2 tập A, B với A = {1,a,2,b,3,c,d}, B = {x,5,y,6,c,1,z}. Số phần tử của tập (A – B) là:

Cho 2 tập A, B với | A | = 100 , | B | = 200 , A ⊆ B . | A ∪ B | | A | = 100 , | B | = 200 , A ⊆ B . | A ∪ B | là:

Cho biết số phần tử của tập A ∩ ( B ∪ C ) A ∩ ( B ∪ C ) nếu mỗi tập có 50 phần tử và các tập hợp đôi một rời nhau.

Cho biết số phần tử của A ∩ ( B ∪ C ) A ∩ ( B ∪ C ) nếu mỗi tập có 100 phần tử và nếu có 50 phần tử chung của mỗi cặp 2 tập và có 10 phần tử chung của cả 3 tập.

Cho X = {1,2,3,4,5,6,7,8,9} A = {1,2,3,8}, B = {2,4,8,9}, C = {6,7,8,9}. Tìm xâu bit biểu diễn tập: ( A ∩ B ) ∪ C ( A ∩ B ) ∪ C

Cho X = {1,2,3,4,5,6,7,8,9}, A = {1,4,5,8,9} Tìm xâu bit biểu diễn tập A¯ trên X:

Cho X = {1,2,3,4,5,6,7,8,9}. Xâu bit biểu diễn tập A là: 111001011, xâu bit biểu diễn tập B là 010111001. Tìm xâu bit biểu diễn tập A ∩ B . A ∩ B .

Cho tập A = {a,b,5}. Hỏi tập nào là tập lũy thừa của tập A?

Xét các hàm từ R tới R, hàm nào dưới đây là khả nghịch:

Cho hàm số f(x)=2x và g(x)=4x2+1, với x ∈ ℝ . Khi đó f.g(-2) bằng:

Cho tập A = {1, 2, 3, {a,4}, {a,b,c}, ∅ ∅ }. Lực lượng của A bằng:

Cho tập S = {a, b, c,d} khi đó số phần tử của tập lũy thừa của tập S là:

Cho 2 tập hợp: A= {1,2,3,4,5,a, hoa, xe máy, dog, táo, mận} B = {hoa, 3,4 , táo} Tập nào trong các tập dưới đây là tập con của tập BxA:

Cho 2 tập A={1, 2, 3}, B={a, b, c, 2}. Trong số các tập dưới đây, tập nào là một quan hệ 2 ngôi từ A tới B?

Xác định tập lũy thừa của tập A = {toán, văn}.

Xác định tích đề các của 2 tập A = {9,x,y} và B = {9,a}:

Số các xâu nhị phân có độ dài là 10 là:

Số các xâu nhị phân có độ dài nhỏ hơn hoặc bằng 10 là:

Số hàm từ tập A có k phần tử vào tập B có n phần tử là:

Có bao nhiêu xâu nhị phân độ dài là 8 hoặc bắt đầu bởi 00 hoặc kết thúc bởi 11.

Có bao nhiêu xâu nhị phân độ dài bằng 8 và không chứa 6 số 0 liên tiếp.

Có bao nhiêu xâu nhị phân độ dài bằng 8 bắt đầu bởi 00 và kết thúc bởi 11.

Một sinh viên phải trả lời 8 trong số 10 câu hỏi cho một kỳ thi. Sinh viên này có bao nhiêu sự lựa chọn nếu sinh viên phải trả lời ít nhất 4 trong 5 câu hỏi đầu tiên?

Cho tập A = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19} hỏi ta cần lấy ít nhất bao nhiêu phần tử từ tập A để chắc chắn rằng có một cặp có tổng bằng 20.

Một dãy XXXYYY độ dài 6. X có thể gán bởi một chữ cái. Y có thể gán một chữ số. Có bao nhiêu dãy được thành lập theo cách trên:

Một phiếu trắc nghiệm đa lựa chọn gồm 10 câu hỏi. Mỗi câu có 4 phương án trả lời. Có bao nhiêu cách điền một phiếu trắc nghiệm nếu mọi câu hỏi đều được trả lời.

Một phiếu trắc nghiệm đa lựa chọn gồm 10 câu hỏi. Mỗi câu có 4 phương án trả lời. Có bao nhiêu cách điền một phiếu trắc nghiệm nếu câu hỏi có thể bỏ trống.

Trong lớp CNTT có 50 sinh viên học tiếng Anh; 20 sinh viên học tiếng Pháp và 10 sinh viên học cả Anh và Pháp. Cho biết sĩ số của lớp là 80. Hỏi có bao nhiêu sinh viên không học tiếng Anh, Pháp.

Cho tập A gồm 10 phần tử. Số tập con của tập A là:

Mỗi người sử dụng thẻ ATM đều có mật khẩu dài 4 hoặc 6 ký tự. Trong đó mỗi ký tự là một chữ số. Hỏi có bao nhiêu mật khẩu?

Có bao nhiêu số nguyên dương không lớn hơn 1000 chia hết cho 7 hoặc 11?

Có bao nhiêu số nguyên dương không lớn hơn 1000 không chia hết cho 7 hoặc 11.

Có 8 đội bóng thi đấu vòng tròn. Hỏi phải tổ chức bao nhiêu trận đấu?

Một tập hợp 100 phần tử có bao nhiêu tập con có ít hơn ba phần tử?

Một tập hợp 100 phần tử có bao nhiêu tập con có 2 phần tử?

Có 20 vé số khác nhau trong đó có 3 vé chứa các giải Nhất, Nhì, Ba. Hỏi có bao nhiêu cách trao giải thưởng cho 20 người, mỗi người giữ một vé?

Một tổ bộ môn có 10 nam và 15 nữ. Có bao nhiêu cách chọn một hội đồng gồm 6 ủy viên, trong đó số ủy viên nam gấp đôi số ủy viên nữ?

Công thức nào sau đây đúng. Cho n là số nguyên dương, khi đó ∑k=0nC(n,k) là:

Công thức nào sau đây đúng. Cho n và k là các số nguyên dương với n ≥ k. Khi đó:

Hệ số của x12y13 trong khai triển (x+y)25 là:

Cho n, r là các số nguyên không âm sao cho r ≤ n r ≤ n . Khi đó:

Trong khai triển (x+y)200 có bao nhiêu số hạng?

Tìm hệ số của x9 trong khai triển của (2 - x)20

Có bao nhiêu cách tuyển 5 trong số 10 cầu thủ của một đội quần vợt để đi thi đấu tại một trường khác?

Cho X={1,2,3,4,5,6,7,8,9}, A={1,2,3,8}. Tìm xâu bit biểu diễn tập

Cho quy tắc f: ℝ → ℝ thỏa mãn $f (x) = 2 x^{2} + 5$ . Khi đó f là:

Cho hàm số $f (x) = 2 x$ và $g (x) = 4 x^{2} + 1$ , với x $\in$ ℝ . Khi đó g.f(-2) bằng:

Cho 2 tập hợp:

A = {1,2,3,4,5,a, hoa, xe máy, dog, táo, mận}

B = {hoa, 3,4 , táo}

Tập nào trong các tập dưới đây là tập con của tập AxB:

Cho X = {1,2,3,4,5,6,7,8,9}, A = {1,4,5,8,9} Tìm xâu bit biểu diễn tập $\bar{A}$ trên X:

Cho hàm số $f (x) = 2 x$ và $g (x) = 4 x^{2} + 1$ , với x $\in$ ℝ . Khi đó f.g(-2) bằng:

Công thức nào sau đây đúng. Cho n là số nguyên dương, khi đó $\sum_{k = 0}^{n} C (n, k)$ là:

Hệ số của x¹²y¹³ trong khai triển (x+y)²⁵ là:

Trong khai triển (x+y)²⁰⁰ có bao nhiêu số hạng?

Tìm hệ số của x⁹ trong khai triển của (2 - x)²⁰

Cho hàm số $f (x) = 3 x^{2} + 2 x + 1$ và $g (x) = 5 x - 2$ , với x $\in$ ℝ . Khi đó g.f(2) bằng:

Cho hàm số $f (x) = 3 x^{2} + 2 x + 1$ và $g (x) = 5 x - 2$ , với x $\in$ ℝ . Khi đó g.f(2) bằng:

Cho quan hệ R = {(a,b)| a ≡ b(mod 5)} trên tập {-12, -11, …,11, 12}. Hãy xác định [2] _R?

Cho tập A = { 1, 2, 3, 4, 5, 6 } và quan hệ R ⊆ A x A với:

R= {(1,1), (2,2), (3,3),(4,4), (5,5), (6,6), (1,3), (3,1),(1, 5), (5, 1),(2, 4), (4, 2), (2,6), (6,2), (3,5), (5,3), (4,6), (6,4)}

Ma trận biểu diễn R là:

Cho tập A = {1, 2, 3, 4, 5, 6}. Cho A₁ = {1}, A₂ = {2}, A₃ = {3, 4}, A₄ = {5, 6}. Quan hệ tương đương R trên A sinh ra phân hoạch A₁, A₂, A₃, A₄ là:

Cho tập A = {1, 2, 3, 4, 5, 6}. Cho A₁ = {1, 2, 3}, A₂ = {4, 5}, A₃ = {6}. Quan hệ tương đương R trên A sinh ra phân hoạch A₁, A₂, A₃ là:

Hãy liệt kê quan hệ R trên tập hợp {1,2,3,4,5} biết ma trận biểu diễn như sau:

$[\begin{matrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 \end{matrix}]$

Cho quan hệ R = {(a,b)| a ≡ b(mod 4)} trên tập {-10, -9, …,9, 10}. Hãy xác định [2]_R?