Bài tập Bài 20. Một số ví dụ về cách giải các bài toán thuộc phần động lực học có đáp án

- Thùng chịu tác dụng của bốn lực:

+ Trọng lực  $\overrightarrow{P}$

+ Lực đẩy  $\overrightarrow{F}$

+ Phản lực  $\overrightarrow{N}$

+ Lực ma sát trượt  ${\overrightarrow{F}}_{{}_{ms}}$

- Coi thùng như một chất điểm (hình vẽ)

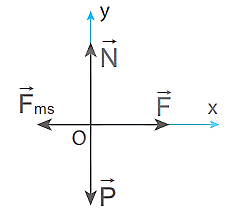
- Áp dụng định luật 2 Newton cho chuyển động của vật theo hai trục Ox, Oy:

  $\left\{\begin{array}{l}Ox:F_x=F-F_{ms}=m.a_x=m.a\\ Oy:F_y=N-P=0\end{array}\right.$

$F_{ms}=\mu .N$

- Giải hệ phương trình:

N = P = mg = 55.9,8 = 539 N

 $F_{ms}=\mu .N=0,35.539=188,65N$

 $a=\frac{F-F_{ms}}{m}=\frac{220-188,65}{55}=0,57m/s^2$

Vậy gia tốc của thùng là 0,57 m/s²

Coi quyển sách là chất điểm, phân tích các lực tác dụng lên quyển sách tại trọng tâm gồm có: trọng lực, phản lực, lực ma sát.

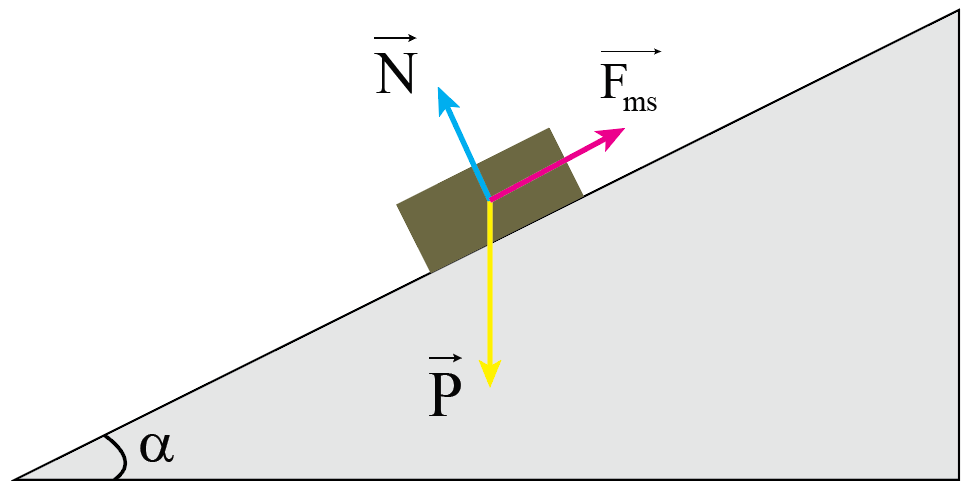
Chọn hệ trục tọa độ Oxy như hình vẽ:

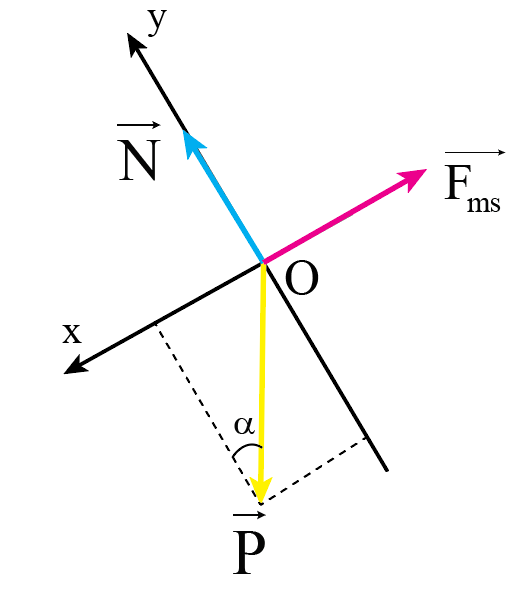
- Áp dụng định luật 2 Newton cho chuyển động của vật theo hai trục Ox, Oy:

 $\left\{\begin{array}{l}Ox:F_x=P.\sin \alpha -F_{ms}=m.a_x=m.a\left(1\right)\\ Oy:F_y=N-P.\cos \alpha =0\left(2\right)\end{array}\right.$

Mà  $F_{ms}=\mu .N$

Giải hệ phương trình có:

Từ (2)  $\Rightarrow N=P.\cos \alpha =mg.\cos \alpha$

 $\Rightarrow F_{ms}=\mu N=\mu mg.\cos \alpha$

Thay vào (1) ta được:

Gia tốc:  $a=\frac{P.\sin \alpha -F_{ms}}{m}=\frac{mg.\sin \alpha -\mu mg.\cos \alpha }{m}=g.\sin \alpha -\mu g.\cos \alpha$

Thay số ta được:  $a=9,8.\sin {30}^0-0,3.9,8.\cos {30}^0=2,35m/s^2$

Coi như con dốc đủ dài, sau 2s quyển sách vẫn chuyển động trên con dốc.

Quãng đường đi được sau 2s:  $s=\frac{1}{2}a{t}^2=\frac{1}{2}.2,{35.2}^2=4,7m$

Coi thùng hàng là chất điểm, phân tích các lực tác dụng lên thùng hàng tại trọng tâm gồm có: lực kéo, trọng lực, phản lực, lực ma sát.

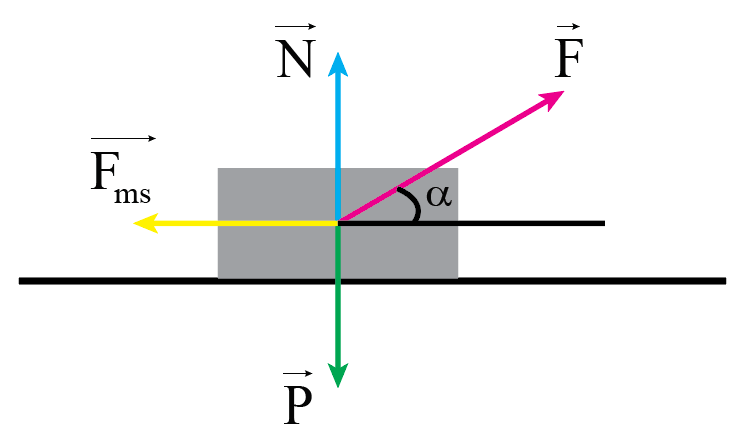
Chọn hệ trục tọa độ Oxy như hình vẽ:

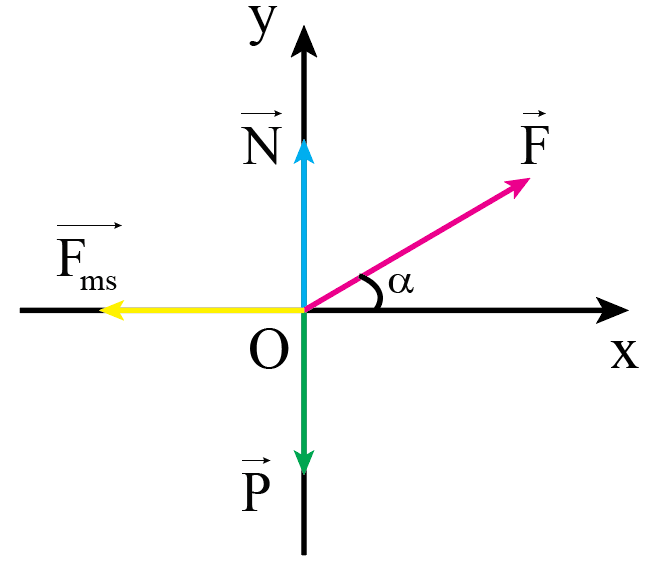
- Vật chuyển động thẳng đều.

- Áp dụng định luật 2 Newton cho chuyển động của vật theo hai trục Ox, Oy:

 $\left\{\begin{array}{l}Ox:F_x=F.\cos \alpha -F_{ms}=m.a_x=0\left(1\right)\\ Oy:F_y=N+F.\sin \alpha -P=0\left(2\right)\end{array}\right.$

Mà  $F_{ms}=\mu .N$

Giải hệ phương trình có:

Từ (2)  $\Rightarrow N=P-F.\sin \alpha =mg-F.\sin \alpha$

 $\Rightarrow F_{ms}=\mu N=\mu mg-\mu F.\sin \alpha$

Thay vào (1) ta được:

 $F.\cos \alpha -\mu mg+\mu F.\sin \alpha =0\Rightarrow F=\frac{\mu mg}{\cos \alpha +\mu .\sin \alpha }=20,3N$

Coi các vật$T_1=T_2=\mu m_{2}g+m_{2}a=30N$ là chất điểm, phân tích các lực tác dụng lên các vật tại trọng tâm của chúng gồm có:

Vật 1: lực kéo, trọng lực, phản lực, lực ma sát, lực căng dây.

Vật 2: lực căng dây, phản lực, lực ma sát, trọng lực.

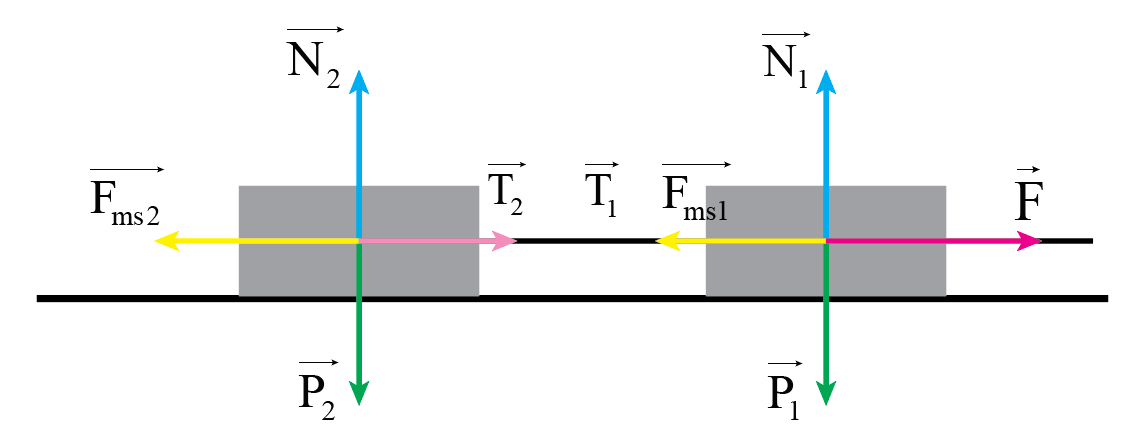
Chọn hệ trục tọa độ Oxy như hình vẽ:

Vật 1:

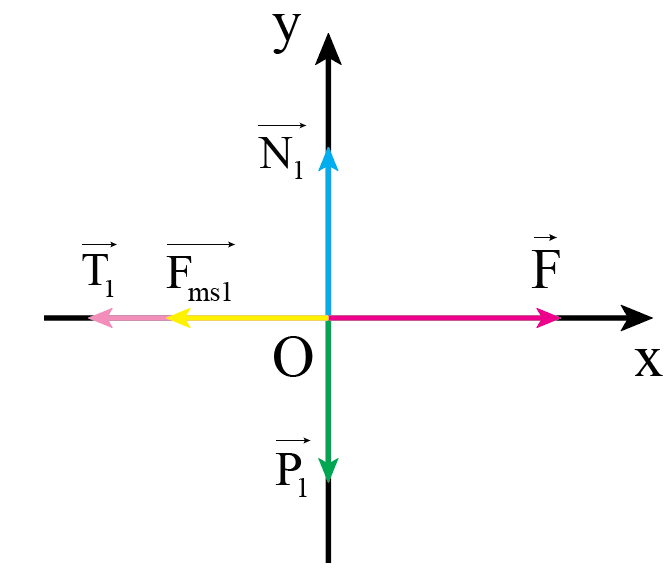
- Áp dụng định luật 2 Newton cho chuyển động của vật 1 theo hai trục Ox, Oy:

 $\left\{\begin{array}{l}Ox:F_x=T_2-F_{ms2}=m_2.a_x=m_2{a}_2\left(3\right)\\ Oy:F_y=N_2-P_2=0\left(4\right)\end{array}\right.$

Mà  $F_{ms2}=\mu .N_2$

Giải hệ phương trình có:

Từ (2) ta được:  $N_1=P_1=m_{1}g$

 $\Rightarrow F_{ms1}=\mu N_1=\mu m_{1}g$

Thay vào (1) ta được:

 $\Rightarrow F-\mu m_{1}g-T_1=m_1{a}_1\Rightarrow T_1=F-\mu m_{1}g-m_1{a}_1$

Vật 2:

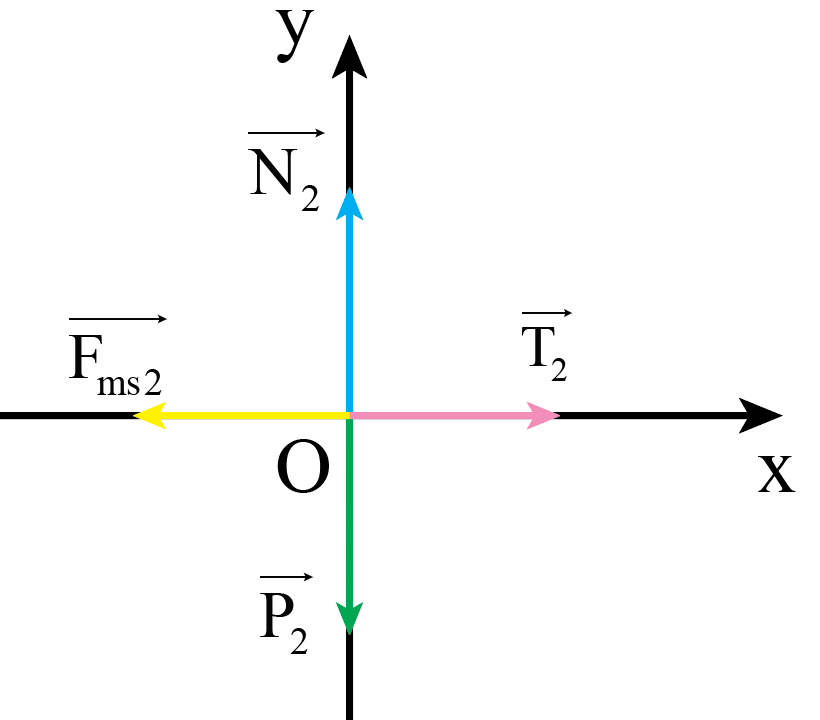
- Áp dụng định luật 2 Newton cho chuyển động của vật 2 theo hai trục Ox, Oy:

 $\left\{\begin{array}{l}Ox:F_x=T_2-F_{ms2}=m_2.a_x=m_2{a}_2\left(3\right)\\ Oy:F_y=N_2-P_2=0\left(4\right)\end{array}\right.$

Mà  $F_{ms2}=\mu .N_2$

Giải hệ phương trình có:

Từ (4) ta được:  $N_2=P_2=m_{2}g$

 $\Rightarrow F_{ms2}=\mu N_2=\mu m_{2}g$

Thay vào (3) ta được:

 $\Rightarrow T_2-\mu m_{2}g=m_2{a}_2\Rightarrow T_2=\mu m_{2}g+m_2{a}_2$

Do hệ 2 vật được nối với nhau bằng một sợi dây không dãn nên ta có:

 $T_1=T_2\Rightarrow F-\mu m_{1}g-m_1{a}_1=\mu m_{2}g+m_2{a}_2$

Bên cạnh đó hệ hai vật chuyển động với cùng gia tốc nên ta có:  $a_1=a_2=a$

 $\Rightarrow F-\mu m_{1}g-m_{1}a=\mu m_{2}g+m_{2}a\Rightarrow a=\frac{F-\mu m_{1}g-\mu m_{2}g}{m_1+m_2}=1,04m/s^2$

Lực căng dây nối:  

Cách khác: có thể viết định luật 2 Newton cho hệ 2 vật vào một phương trình đều được, khi đó biện luận cho lực căng dây, gia tốc để giải ngắn gọn hơn.