Câu hỏi:

08/08/2022 14,311

Một người chơi cầu lông có khuynh hướng phát cầu với góc 30° (so với mặt đất). Hãy tính khoảng cách từ vị trí người này đến vị trí cầu rơi chạm đất (tầm bay xa), biết cầu rời mặt vợt ở độ cao 0,7 m so với mặt đất và vận tốc ban đầu của cầu là 12 m/s (bỏ qua sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng thẳng đứng).

A. 11,456 m;

B. 12,23 m;

C. 13 m;

D. 13,84 m.

Xem lời giải

Câu hỏi trong đề: 12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Hướng dẫn giải:

Đáp án đúng là: D.

Cầu rời mặt vợt ở độ cao 0,7 m so với mặt đất và vận tốc ban đầu của cầu là 12 m/s (bỏ qua sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng thẳng đứng).

Chọn hệ trục tọa độ Oxy

Với g = 9,8 m/s², góc phát cầu α = 30°, vận tốc ban đầu v₀ = 12 m/s, phương trình quỹ đạo của cầu là:

\(y = \frac{{ - 9,8.{x^2}}}{{{{2.12}^2}.co{s^2}{{30}^o}}} + \tan {30^o}.x + 0,7 = - \frac{{49}}{{1080}}{x^2} + \frac{{\sqrt 3 }}{3}x + 0,7\)(với x ≥ 0)\(\)

Khi x = 4, ta có \(y = - \frac{{49}}{{1080}}{.4^2} + \frac{{\sqrt 3 }}{3}.4 + 0,7 \approx 2,283\)> 1,524

Như vậy, cầu đã vượt qua lưới. Điểm rơi của cầu là giao điểm của parabol và trục hoành nên giải phương trình:

\( - \frac{{49}}{{1080}}{x^2} + \frac{{\sqrt 3 }}{3}x + 0,7 = 0\) ta được: x₁ ≈ 13,84 và x₂ ≈ –1,11

Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 13,84 m.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một chiếc cổng hình parabol có phương trình \(y = - \frac{1}{2}{x^2}\). Biết cổng có chiều rộng d = 5 mét. Hãy tính chiều cao h của cổng.

A. 4,45 m;

B. 3,125 m;

C. 4,125 m;

D. 3,25 m.

Lời giải

Hướng dẫn giải:

Đáp án đúng là: B.

Gọi A và B là hai điểm ứng với hai chân cổng như hình vẽ.

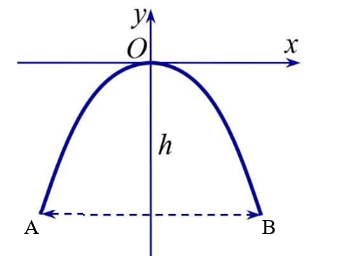
Vì cổng hình parabol có phương trình \(y = - \frac{1}{2}{x^2}\) và cổng có chiều rộng d = 5 m nên:

AB = 5 và hoành độ của A và B lần lượt là \( - \frac{5}{2},\,\,\frac{5}{2}\).

Ta có: \(y = - \frac{1}{2}.{\left( {\frac{5}{2}} \right)^2} = - \frac{1}{2}.{\left( { - \frac{5}{2}} \right)^2} = \frac{{ - 25}}{8}\)

Do đó, \(A\left( {\frac{{ - 5}}{2};\frac{{ - 25}}{8}} \right)\) và \(B\left( {\frac{5}{2};\frac{{ - 25}}{8}} \right)\).

Chiều cao của cổng chính là giá trị tuyệt đối tung độ của A và B hay h = \(\left| {\frac{{ - 25}}{8}} \right| = \frac{{25}}{8} = 3,125\) (m).

Câu 2

Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol. Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có độ cao 43 m so với mặt đất, người ta thả một sợi dây chạm đất. Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10 m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch.

A. 185,6 m;

B. 184 m;

C. 180 m;

D. 175,6 m.

Lời giải

Hướng dẫn giải:

Đáp án đúng là: A.

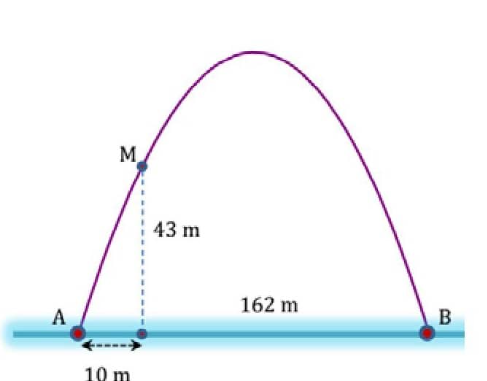
Chọn hệ trục tọa độ Oxy như hình, A ≡ O.

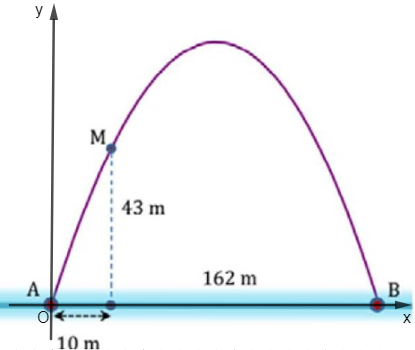
Parabol (P) có phương trình dạng: y = ax² + bx + c (a ≠ 0).

Parabol đi qua điểm A(0; 0), B(162; 0), M(10; 43) nên ta có:

\(\left\{ \begin{array}{l}c = 0\\{162^2}a + 162b + c = 0\\{10^2}a + 10b + c = 43\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 0\\a = \frac{{ - 43}}{{1520}}\\b = \frac{{3483}}{{760}}\end{array} \right.\)

Do đó, phương trình của (P) là: \(y = - \frac{{43}}{{1520}}{x^2} + \frac{{3483}}{{760}}x\)

Do đó, chiều cao của cổng là tung độ của đỉnh parabol và là:

\(h = - \frac{\Delta }{{4a}} = - \frac{{{b^2} - 4ac}}{{4a}} = - \frac{{{{\left( {\frac{{3483}}{{760}}} \right)}^2} - 4.\left( {\frac{{ - 43}}{{1520}}} \right).0}}{{4.\left( {\frac{{ - 43}}{{1520}}} \right)}} \approx 185,6\) (m).

Câu 3