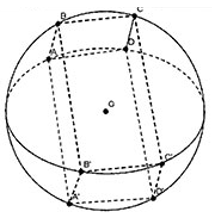
Cho hình hộp chữ nhật ABCDA'B'C'D' nội tiếp mặt cầu tâm O (các đỉnh của hình hộp chữ chữ nhật nằm trên mặt cầu). Các kích thước của hình hộp chữ nhật lần lượt là a, b, c. Gọi $S_{1}$ là diện tích toàn phần của hình hộp chữ nhật, $S_{2}$ là diện tích mặt cầu. Tìm mối liên hệ giữa a,b, c để tỉ lệ $\frac{S_{1}}{S_{2}}$ lớn nhất.

Xem lời giải

Câu hỏi trong đề: Bộ đề Ôn tập Toán 9 thi vào 10 năm 2018 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có $S_{1} = 2 (a b + a c + b c),$

Description: ÄaÌp aÌn ÄÃªÌ thi vaÌo lÆ¡Ìp 10 mÃ´n ToaÌn $S_{2} = 4 π \frac{(a^{2} + b^{2} + c^{2})}{4} = π (a^{2} + b^{2} + c^{2}) .$

Do đó:

$\frac{S_{1}}{S_{2}} = \frac{2 (a b + a c + b c)}{π (a^{2} + b^{2} + c^{2})} = \frac{2 (2 a b + 2 a c + 2 b c)}{π (2 a^{2} + 2 b^{2} + 2 c^{2})}$

Mặt khác $\frac{2 (2 a b + 2 a c + 2 b c)}{π (2 a^{2} + 2 b^{2} + 2 c^{2})} \leq \frac{2}{π}$

Do đó, tỉ lệ $\frac{S_{1}}{S_{2}}$ lớn nhất là $\frac{2}{π} .$ Điều này xảy ra khi và chỉ khi $a = b = c .$

Cho hình hộp chữ nhật ABCDA'B'C'D' nội tiếp mặt cầu tâm O (các đỉnh của hình hộp chữ chữ nhật nằm trên mặt cầu) (ảnh 1)

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Biết rằng các số x, y thỏa mãn điều kiện x+y=1. Tìm giá trị nhỏ nhất của biểu thức $C = x^{2} + y^{2} + x y$

Xem đáp án

Lời giải

Cách 1:

Nhận xét: trong tất cả các điều kiện và biểu thức, vai trò của x, y đều bình đẳng nên C đạt GTNN khi x=y. Do đó, ta biến đổi như bên dưới.

Ta có: $C = x^{2} + y^{2} + x y = a {(x + y)}^{2} + b {(x - y)}^{2} = (a + b) (x^{2} + y^{2}) + 2 (a - b) x y$ .

Suy ra $\{\begin{cases} a + b = 1 \\ a - b = \frac{1}{2} \end{cases} \Leftrightarrow \{\begin{cases} a = \frac{3}{4} \\ b = \frac{1}{4} \end{cases}$ .

Hay ta có: $C = \frac{3}{4} {(x + y)}^{2} + \frac{1}{4} {(x - y)}^{2} = \frac{3}{4} .1 + \frac{1}{4} {(x - y)}^{2} \geq \frac{3}{4}$

Dấu “=” xảy ra khi $\{\begin{cases} x = y \\ x + y = 1 \end{cases} \Leftrightarrow x = y = \frac{1}{2}$ .

Vậy, giá trị nhỏ nhất của C là $\min C = \frac{3}{4}$ khi $x = y = \frac{1}{2}$ .

Cách 2:

Do $x + y = 1 \Rightarrow y = 1 - x$ . Khi đó, ta có:

$C = x^{2} + y^{2} + x y = x^{2} + {(1 - x)}^{2} + x (1 - x) = x^{2} - x + 1 = {(x - \frac{1}{2})}^{2} + \frac{3}{4} \geq \frac{3}{4}$ .

Dấu “=” xảy ra khi $\{\begin{cases} x = \frac{1}{2} \\ x + y = 1 \end{cases} \Leftrightarrow x = y = \frac{1}{2}$ .

Vậy, $\min C = \frac{3}{4}$ khi $x = y = \frac{1}{2}$ .

Câu 2

Cho x, y là các số dương thỏa mãn điều kiện $x + y \geq 6$ . Tìm giá trị nhỏ nhất của biểu thức $P = 3 x + 2 y + \frac{6}{x} + \frac{8}{y}$

Xem đáp án

Lời giải

- Dùng máy tính casio ta chọn được điểm rơi tại x = 2, y = 4. Nên ta có:

$P = 3 x + 2 y + \frac{6}{x} + \frac{8}{y} = (\frac{3 x}{2} + \frac{6}{x}) + (\frac{2 y}{4} + \frac{8}{y}) + 1, 5 x + 1, 5 y$

- Áp dụng BĐT Cô-si cho từng cặp số trong ngoặc ta được

$P \geq 6 + 4 + 1, 5 (x + y) = 6 + 4 + 1, 5.6 = 19$

Dấu bằng xảy ra khi: $\{\begin{cases} \frac{3 x}{2} = \frac{6}{x} \\ \frac{2 y}{4} = \frac{8}{y} \\ x + y \geq 6 \end{cases} \Leftrightarrow \{\begin{cases} x = \pm 2 \\ y = \pm 4 \\ x + y \geq 6 \end{cases} \Leftrightarrow \{\begin{cases} x = 2 \\ y = 4 \end{cases}$

Vậy P_min= 19 tại $\{\begin{cases} x = 2 \\ y = 4 \end{cases}$ .

Câu 3