Câu hỏi trong đề: Bộ đề Ôn tập Toán 9 thi vào 10 năm 2018 có đáp án !!
Quảng cáo
Trả lời:
Đặt
Từ giả thiết, ta có:
Áp dụng bất đẳng thức Cauchy cho ba số thực dương, ta có:
(1).
Tương tự, ta có:
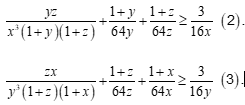
Cộng (1), (2), (3), ta được:
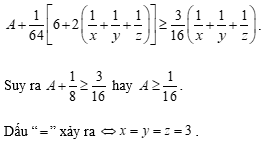
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Cách 1:
Nhận xét: trong tất cả các điều kiện và biểu thức, vai trò của x, y đều bình đẳng nên C đạt GTNN khi x=y. Do đó, ta biến đổi như bên dưới.
Ta có: .
Suy ra .
Hay ta có:
Dấu “=” xảy ra khi .
Vậy, giá trị nhỏ nhất của C là khi .
Cách 2:
Do . Khi đó, ta có:
.
Dấu “=” xảy ra khi .
Vậy, khi .
Lời giải
- Dùng máy tính casio ta chọn được điểm rơi tại x = 2, y = 4. Nên ta có:
- Áp dụng BĐT Cô-si cho từng cặp số trong ngoặc ta được
Dấu bằng xảy ra khi:
Vậy Pmin = 19 tại .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.