Hai người A và B đứng cùng bờ sông nhìn ra một cồn nổi giữa sông. Người A nhìn ra cồn với 1 góc 430 so với bờ sông, người B nhìn ra cồn với 1 góc 280 so với bờ sông, 2 người đứng cách nhau 250m. Hỏi...

Hình vẽ minh họa bài toán: Xét ∆AHC vuông tại A, ta có: tan CAH^=CHAH (tỉ số lượng giác của góc nhọn) ⇒AH=CH=CHtan430 m (1) Xét ∆BHC vuông tại A, ta có: tan CBH^=CHBH (tỉ số lượng giác của góc nhọn) ⇒BH=CHtan CBH^=CHtan280 (2) Từ (1) và (2) ⇒AH+BH=CHtan430+CHtan280⇔AB=CH.1tan430+1tan280⇔250=CH.1tan430+1tan280 ⇔CH=2501tan430+1tan280≈84,66m Vậy cồn cách bờ sông hai người đang đứng là 84,66m

Câu hỏi:

13/07/2024 37,697

Hai người A và B đứng cùng bờ sông nhìn ra một cồn nổi giữa sông. Người A nhìn ra cồn với 1 góc 43⁰ so với bờ sông, người B nhìn ra cồn với 1 góc 28⁰ so với bờ sông, 2 người đứng cách nhau 250m. Hỏi cồn cách bờ sông hai người đang đứng là bao nhiêu m?

Xem lời giải

Câu hỏi trong đề: Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Hình vẽ minh họa bài toán:

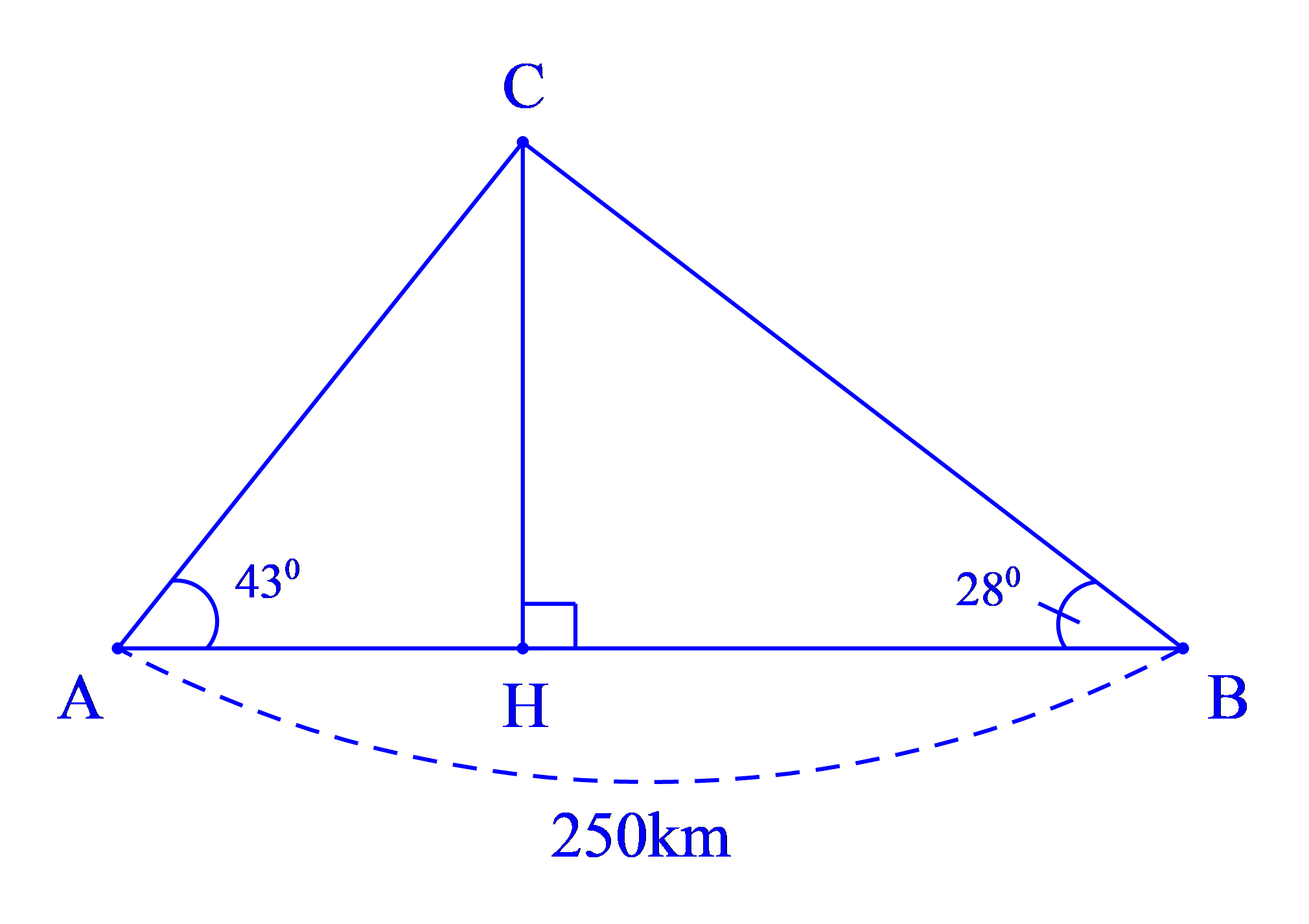
Media VietJack

Xét ∆AHC vuông tại A, ta có:

$\tan \hat{C A H} = \frac{CH}{AH}$ (tỉ số lượng giác của góc nhọn)

$\Rightarrow AH = \frac{CH}{} = \frac{CH}{{tan43}^{0}} (m)$ (1)

Xét ∆BHC vuông tại A, ta có:

$\tan \hat{C B H} = \frac{CH}{BH}$ (tỉ số lượng giác của góc nhọn)

$\Rightarrow BH = \frac{CH}{\tan \hat{C B H}} = \frac{CH}{{tan28}^{0}}$ (2)

Từ (1) và (2) $\Rightarrow AH + BH = \frac{CH}{{tan43}^{0}} + \frac{CH}{{tan28}^{0}}$ $\Leftrightarrow AB = CH. (\frac{1}{{tan43}^{0}} + \frac{1}{{tan28}^{0}}) \Leftrightarrow 250 = CH. (\frac{1}{{tan43}^{0}} + \frac{1}{{tan28}^{0}})$

$\Leftrightarrow CH = \frac{250}{\frac{1}{{tan43}^{0}} + \frac{1}{{tan28}^{0}}} \approx 84,66m$

Vậy cồn cách bờ sông hai người đang đứng là 84,66m

Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trên nóc của một tòa nhà có một cột ăng-ten cao 5m. Từ vị trí quan sát A cao 7m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50⁰ và 40⁰ so với phương nằm ngang. Tính chiều cao của tòa nhà.

Xem đáp án

Lời giải

Dựa vào hình vẽ bài toán, ta có:

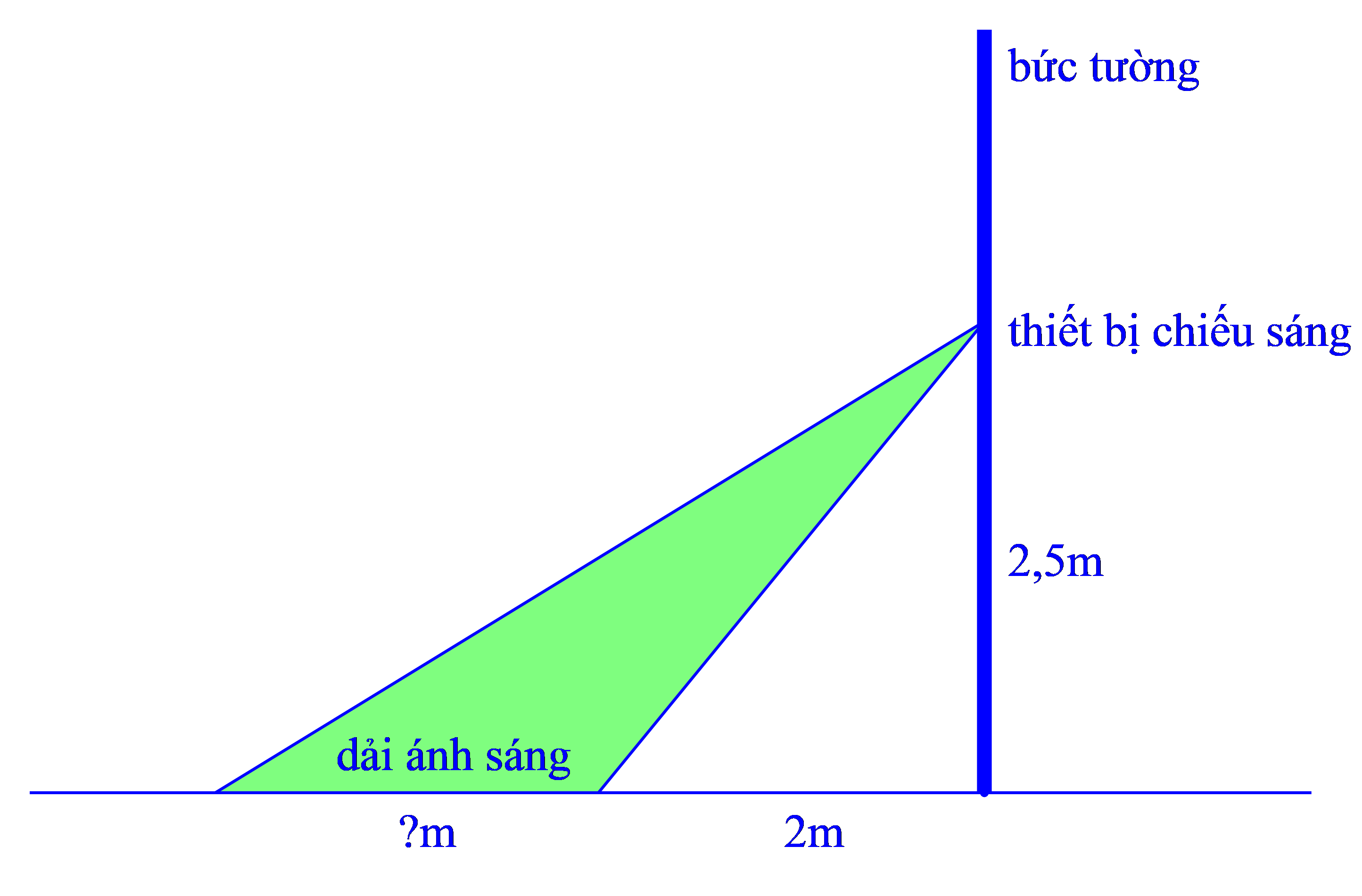
BC = 5m

AD = EH = 7m

$\hat{B A E} = 50^{0}; \hat{C A E} = = 40^{0}$

$\hat{C E A} = \hat{B E A} = 90^{0}$

Xét ∆CAE vuông tại E, ta có:

$tanCAE = \frac{CE}{AE}$ (tỉ số lượng giác của góc nhọn)

$\Rightarrow CE = AE.tanCAE = {AE.tan40}^{0} (m)$ (1)

Xét ∆BAE vuông tại E, ta có:

$tanBAE = \frac{BE}{AE}$ (tỉ số lượng giác của góc nhọn)

$\Rightarrow BE = AE.tanBAE = {AE.tan50}^{0} (m)$ (2)

Từ (1) và (2) $\Rightarrow BE - CE = {AE.tan50}^{0} - {AE.tan40}^{0}$

$\begin{array}{l} \Leftrightarrow BC = AE. ({tan50}^{0} - {tan40}^{0}) \\ \Leftrightarrow 5 = AE. ({tan50}^{0} - {tan40}^{0}) \\ \Leftrightarrow AE = \frac{5}{{tan50}^{0} - {tan40}^{0}} (m) \end{array}$

Từ (1) $\Rightarrow CE = \frac{5}{{tan50}^{0} - {tan40}^{0}} {.tan40}^{0} (m)$

$\Rightarrow BH = BC + CE + EH = 5 + \frac{{5.tan40}^{0}}{{tan50}^{0} - {tan40}^{0}} + 7 \approx 23,9m$

Vậy chiều cao của tòa nhà là 23,9m

Câu 2

Một người quan sát đứng cách một cái tháp 10m, nhìn thẳng đỉnh tháp và chân tháp lần lượt dưới 1 góc 55⁰ và 10⁰ so với phương ngang của mặt đất. Hãy tính chiều cao của tháp.

Xem đáp án

Lời giải

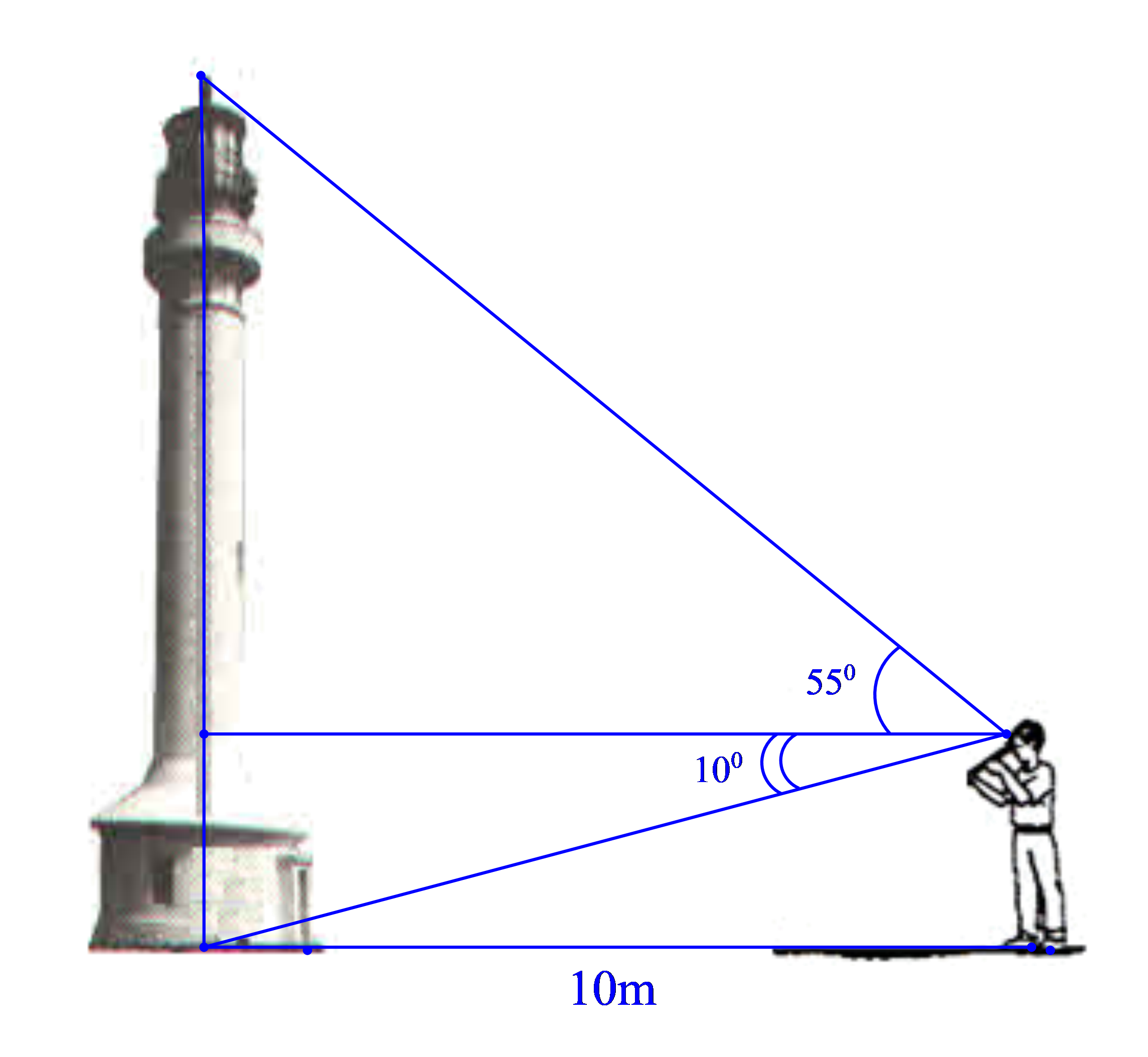
Hình vẽ minh họa bài toán:

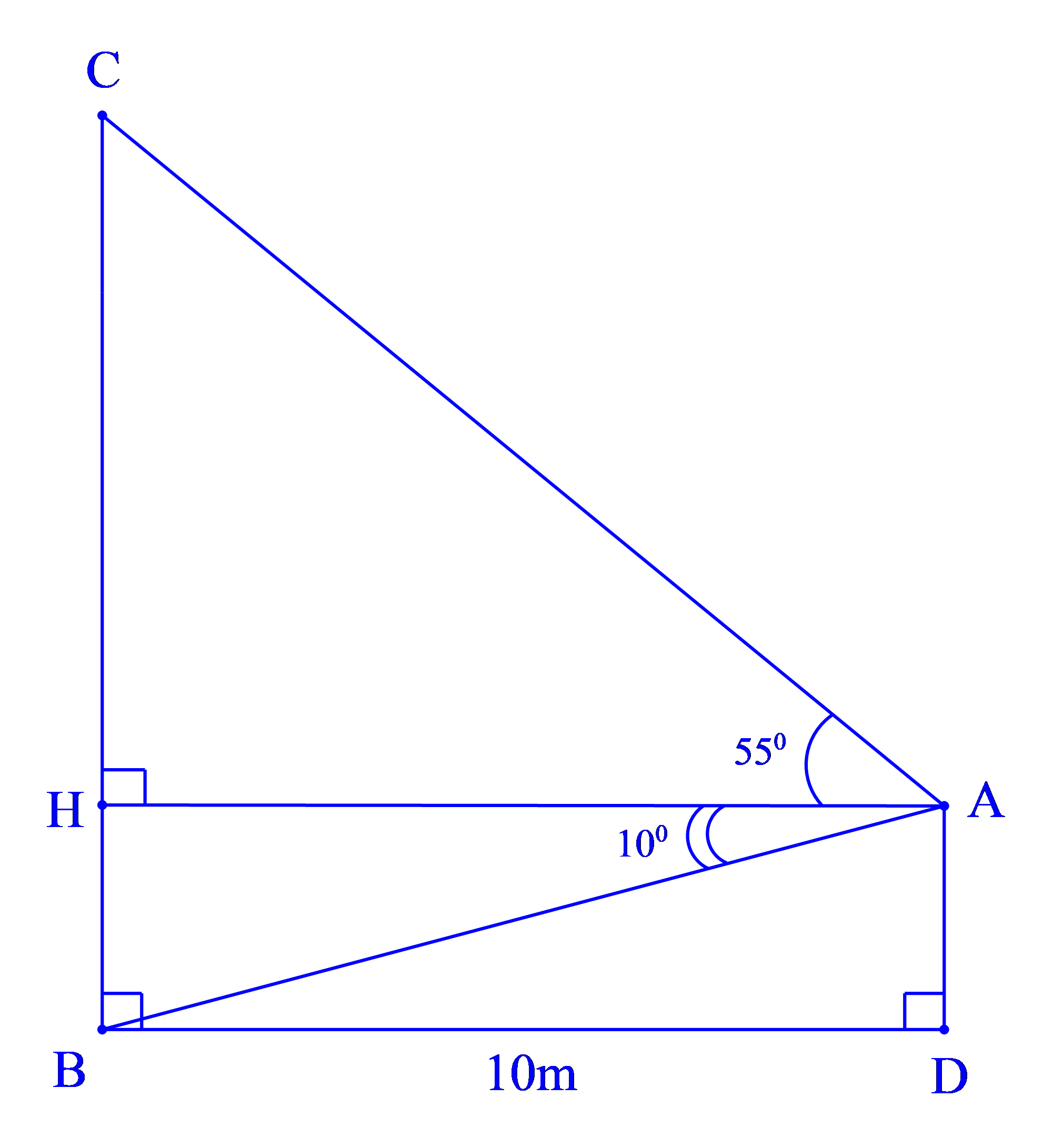
Media VietJack

Dựa vào hình vẽ minh họa, ta có: AH = BD = 10m

Xét ∆AHB vuông tại H, ta có:

$tanBAH = \frac{BH}{AH}$ (tỉ số lượng giác của góc nhọn)

$\Rightarrow BH = AH.tanBAH = {10.tan10}^{0} (m)$

Xét ∆AHC vuông tại H, ta có:

$tanCAH = \frac{CH}{AH}$ (tỉ số lượng giác của góc nhọn)

$\Rightarrow CH = AH.tanCAH = {10.tan55}^{0} (m)$

Ta có: $BC = BH + CH = {10.tan10}^{0} + {10.tan55}^{0} \approx 16m$

Vậy chiều cao của tháp là 16m

Câu 3

Một máy bay đang bay ở độ cao 12km. Khi bay hạ cánh xuống mặt đất, đường đi của máy bay tạo một góc nghiêng so với mặt đất.

a) Nếu cách sân bay 320km máy bay bắt đầu hạ cánh thì góc nghiêng là bao nhiêu (làm tròn đến phút)?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tính lượng vải cần mua để tạo ra nón của chú Hề trong hình bên. Biết rằng tỉ lệ khâu hao vải khi may nón là 15%.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một người thợ sử dụng thước ngắm có góc vuông để đo chiều cao của một cây dừa, với các kích thước đo được như hình bên. Khoảng cách từ vị trí gốc cây đến vị trí chân của người thợ là 4,8m và từ vị trí chân đứng thẳng trên mặt đất đến mắt của người ngắm là 1,6m. Hỏi với các kích thước trên thì người thợ đo được chiều cao của cây đó là bao nhiêu? (làm tròn đến mét).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Người ta cần lắp đặt một thiết bị chiếu sáng gắn trên tường cho một phòng triển lãm. Thiết bị này có góc chiếu sáng là 20⁰ và cần đặt cao hơn mặt đất là 2,5m. Người ta đặt thiết bị này sát tường và canh chỉnh sao cho trên mặt đất dải ánh sáng bắt đầu từ vị trí cách tường 2m. Hãy tính độ dài vùng được chiếu sáng trên mặt đất.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Thang xếp chữ A gồm 2 thang đơn tựa vào nhau. Để an toàn, mỗi thang đơn tạo với mặt đất một góc khoảng 75⁰. Nếu muốn tạo một thang xếp chữ A cao 2m tính từ mặt đất thì mỗi thang đơn phải dài bao nhiêu?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Trên nóc của một tòa nhà có một cột ăng-ten cao 5m. Từ vị trí quan sát A cao 7m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50⁰ và 40⁰ so với phương nằm ngang. Tính chiều cao của tòa nhà.

Một người quan sát đứng cách một cái tháp 10m, nhìn thẳng đỉnh tháp và chân tháp lần lượt dưới 1 góc 55⁰ và 10⁰ so với phương ngang của mặt đất. Hãy tính chiều cao của tháp.

Một máy bay đang bay ở độ cao 12km. Khi bay hạ cánh xuống mặt đất, đường đi của máy bay tạo một góc nghiêng so với mặt đất.

a) Nếu cách sân bay 320km máy bay bắt đầu hạ cánh thì góc nghiêng là bao nhiêu (làm tròn đến phút)?

Thang xếp chữ A gồm 2 thang đơn tựa vào nhau. Để an toàn, mỗi thang đơn tạo với mặt đất một góc khoảng 75⁰. Nếu muốn tạo một thang xếp chữ A cao 2m tính từ mặt đất thì mỗi thang đơn phải dài bao nhiêu?