Câu hỏi:
12/07/2024 1,038
Người ta làm một vườn hoa gồm hai hình tròn tâm A và tâm B tiếp xúc ngoài với nhau. Cho biết khoảng cách AB = 5m và diện tích của vườn hoa là m2. Tính bán kính mỗi hình tròn.
Người ta làm một vườn hoa gồm hai hình tròn tâm A và tâm B tiếp xúc ngoài với nhau. Cho biết khoảng cách AB = 5m và diện tích của vườn hoa là m2. Tính bán kính mỗi hình tròn.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi lần lượt là bán kính của hình tròn (A) và (B)
Theo đề bài, ta có hệ phương trình:
Theo đề bài, ta có hệ phương trình:
Thay (1) vào (2) ta được
Ta giải phương trình (*) được 2 nghiệm là: hoặc
Thay vào (1) ta được (nhận)
Thay vào (1) ta được (loại)
Vậy bán kính hình tròn (A) là 3,2m và bán kính của hình tròn (B) là 1,8m.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
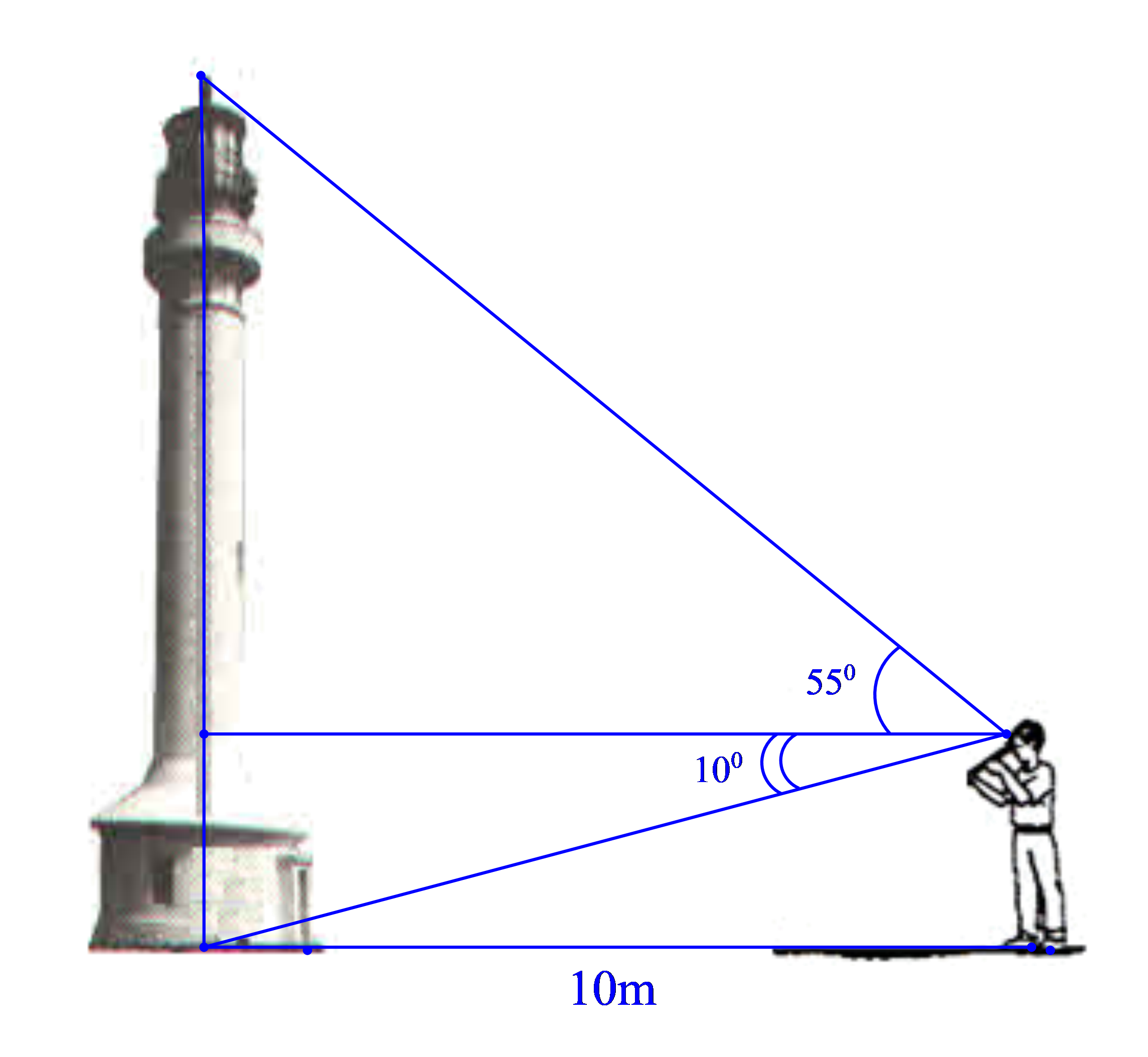
Hình vẽ minh họa bài toán:
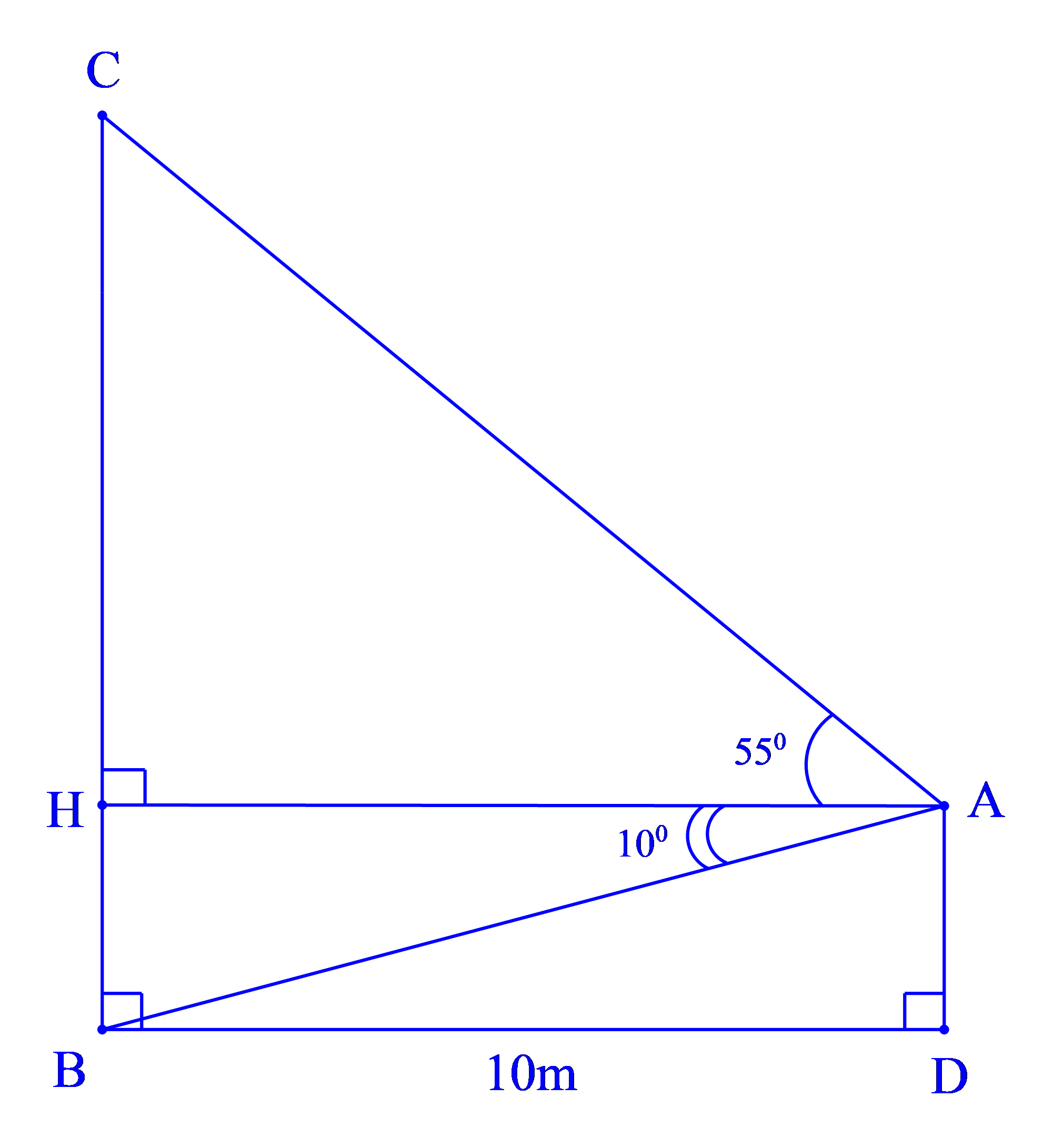
Dựa vào hình vẽ minh họa, ta có: AH = BD = 10m
Xét ∆AHB vuông tại H, ta có:
(tỉ số lượng giác của góc nhọn)
Xét ∆AHC vuông tại H, ta có:
(tỉ số lượng giác của góc nhọn)
Ta có:
Vậy chiều cao của tháp là 16m
Lời giải
a) Hình vẽ minh họa bài toán:
Xét ∆ABC vuông tại A, ta có:
(tỉ số lượng giác của góc nhọn)
Vậy góc nghiêng là
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo