Cho tam giác đường phân giác BN và tâm O của đường tròn nội tiếp trong tam giác. Từ A kẻ một tia vuông góc với tia BN, cắt BC tại H. Chứng minh bốn điểm A; O; H; C nằm trên một đường tròn.

Câu hỏi trong đề: Trắc nghiệm Chuyên đề toán 9 Chuyên đề 10: Rèn luyện kĩ năng tìm lời giải bài toán hình học có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Trường hợp 1: H và O nằm cùng phía với AC

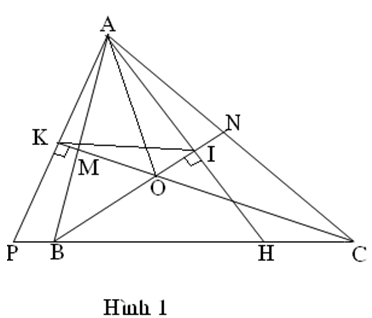
Cho tam giác đường phân giác BN và tâm O của đường tròn nội tiếp trong tam giác. (ảnh 1)

Trường hợp 2: H và O nằm khác phía với AC

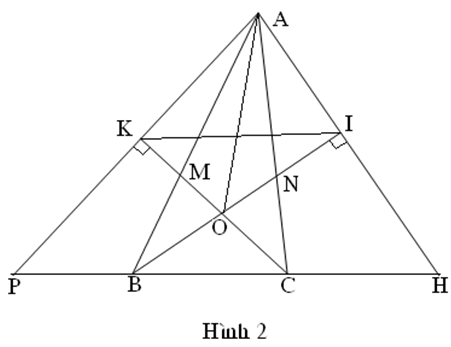
Cho tam giác đường phân giác BN và tâm O của đường tròn nội tiếp trong tam giác. (ảnh 2)

Gợi ý: Gọi I là giao điểm của AH và BN. Kẻ AP vuông góc với CO cắt AB tại P. M là giao điểm của OC và AB, K là giao điểm của OC và AP.

Cách giải 1:
Xét $△$ ACP có CK vừa là phân giác vừa là đường cao nên CK cũng là đường trung tuyến, đường trung trực => KA = KP (1)
Xét ABH có BI vừa là phân giác vừa là đường cao nên BI cũng là đường trung tuyến, đường trung trực => IA = IH (2)
Từ (1) và (2) ta có: IK là đường trung bình trong tam giác APH
$\Rightarrow \hat{I K O} = \hat{O C H}$ ( Hình 1)
Hoặc $\hat{I K O} + \hat{O C H} = 180^{\circ}$ (Hình 2)
Xét tứ giác AKOI có $\hat{I} = \hat{K} = 90^{\circ}$ => AKOI là tứ giác nội tiếp Tứ giác AOHC nội tiếp được => A; O; H; C cùng nằm trên một đường tròn.

Cách giải 2:
Ta có BN là đường trung trực của AH $\Rightarrow \hat{B H O} = \hat{B A O}$ mà $\hat{B A O} = \hat{O A C}$ nên $\hat{B H O} = \hat{O A C}$ => Tứ giác AOHC nội tiếp được. => A; O; H; C cùng nằm trên một đường tròn.

Cách giải 3:
$△$ ABI là tam giác vuông nên $\hat{I B A} + \hat{B A I} = 180^{\circ}$ hay $\hat{I B A} + \hat{B A O} + \hat{O A I} = 180^{\circ}$ Suy ra: $\hat{O A I} + \frac{\hat{B}}{2} + \frac{\hat{A}}{2} = 90^{\circ}$ => $\hat{O A I}$ bằng (hoặc bù) với góc $\hat{O C H} \Rightarrow$ Tứ giác AOHC nội tiếp được => A; O; H; C cùng nằm trên một đường tròn.

Cách giải 4:
* Đối với (Hình 1) ta có $\hat{A H C} = 90^{\circ} + \frac{\hat{B}}{2}$ Góc ngoài trong tam giác
$\hat{A O C} = 90^{\circ} + \frac{\hat{B}}{2}$ (Vì O là tâm của đường tròn nội tiếp)
$\Rightarrow \hat{A H C} = \hat{A O C} \Rightarrow$ Tứ giác AOHC nội tiếp được => A; O; H; C cùng nằm trên một đường tròn.
* Đối với (Hình 2) Xét trong tam giác IBH ta có $\hat{A H C} = 90^{\circ} - \frac{\hat{B}}{2}$
$\hat{A O C} = 90^{\circ} + \frac{\hat{B}}{2}$ (Vì O là tâm của đường tròn nội tiếp) $\Rightarrow \hat{A H C} + \hat{A O C} = 180^{\circ}$
Tứ giác AOHC nội tiếp được => A; O; H; C cùng nằm trên một đường tròn.

Cách giải 5:
Ta có $\hat{A O N} = \frac{\hat{A} + \hat{B}}{2}$ (Góc ngoài ở đỉnh O của tam giác AOB)
$\Rightarrow \hat{A O H} = \hat{A} + \hat{B} \Rightarrow \hat{A O H} + \hat{A C H} = 180^{\circ}$ (Hình 1)
hoặc $\hat{O A H} = \hat{A C H} = \hat{A} + \hat{B}$ (Hình 2)
=> Tứ giác AOHC nội tiếp được => A; O; H; C cùng nằm trên một đường tròn

Nhà sách vietjack

Xem thêm kho sách »

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Siêu tiết kiệm - Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.