✕

✨ Đăng kí VIP để truy cập không giới hạn. Đăng ký ngay

Câu hỏi:

19/08/2025 1,680

Trên cung BC của đường tròn ngoại tiếp tam giác đều ABC lấy một điểm P tuỳ ý. Các đoạn thẳng AP và BC cắt nhau tại điểm Q. Chứng minh rằng: $\frac{1}{P Q} = \frac{1}{P B} - \frac{1}{P C}$

Xem lời giải

Câu hỏi trong đề: Trắc nghiệm Chuyên đề toán 9 Chuyên đề 10: Rèn luyện kĩ năng tìm lời giải bài toán hình học có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Cách giải 1: (Hình 1)

Trên cung BC của đường tròn ngoại tiếp tam giác đều ABC lấy một điểm P tuỳ ý. Các đoạn thẳng AP và BC cắt nhau tại điểm Q (ảnh 1)

Trên đoạn AP lấy hai điểm N và M sao cho BN = BP và PM = PC

Khi đó ta có các tam giác BNP và tam giác MPC là các tam giác cân

Vì

\hat{A P B} = \hat{A C B} = 60^{\circ}

và

\hat{M P C} = \hat{A B C} = 60^{\circ}

(Các góc nội tiếp cùng chắn một cung). Suy ra tam giác BNP và tam giác MPC là các tam giác đều

Xét hai tam giác

△

CQP và

△

BQN có:

\hat{B Q N} = \hat{C Q P}

(Hai góc đổi đỉnh)

\hat{B N Q} = \hat{C P Q} = 60^{\circ}

Nên

△ C Q P ~ △ B Q N \Rightarrow \frac{C P}{P Q} = \frac{B N}{N Q} = \frac{B N}{B N - P Q} \Rightarrow \frac{1}{C P} = \frac{B N - P Q}{P Q . B N}

\frac{1}{P Q} = \frac{1}{P B} - \frac{1}{P C}

(Đpcm)

Cách giải 2: (Hình 2)

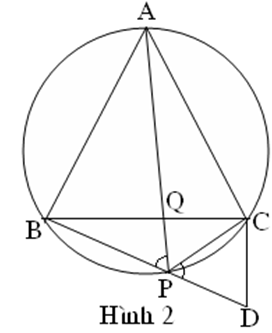
Trên cung BC của đường tròn ngoại tiếp tam giác đều ABC lấy một điểm P tuỳ ý. Các đoạn thẳng AP và BC cắt nhau tại điểm Q (ảnh 2)

Trên tia BP lấy một điểm D sao cho PD = PC
Ta có: $\hat{C P D} = 60^{\circ}$ ( Vì $\hat{C P B} = 120^{\circ}$ góc nội tiếp chắn cung $120^{\circ}$ )
nên tam giác CPD là tam giác đều $\Rightarrow \hat{A P B} = \hat{C D P} = 60^{\circ}$
Vì vậy AP // CD $\Rightarrow △$ BPQ $~ △$ BDC.

$\Rightarrow \frac{B P}{P Q} = \frac{B D}{C D} = \frac{B P + P C}{C P} \Rightarrow \frac{1}{P Q} = \frac{B P + P C}{C P . B P} \Rightarrow \frac{1}{P Q} = \frac{1}{B P} + \frac{1}{C P}$
=> $\frac{1}{P Q} = \frac{1}{P B} - \frac{1}{P C}$ (Đpcm)

Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Xem thêm các câu hỏi khác »