Cho tam giác nhọn ABC nội tiếp đường tròn (O). Từ đỉnh A ta kẻ đường cao AH (H thuộc BC). Chứng minh rằng .
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Từ đỉnh A ta kẻ đường cao AH (H thuộc BC). Chứng minh rằng .
Quảng cáo
Trả lời:
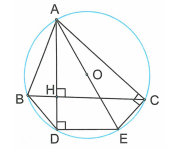
Kẻ đường kính AE của đường tròn (O). Ta thấy (góc nội tiếp chắn nửa đường tròn).
Từ đó . (1)
Theo giả thiết bài ra, ta có: . (2)
Lại vì (cùng chắn ) (3)
Từ (1), (2) và (3) suy ra (đpcm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
<=> <=> cân tại D <=>
Giải chi tiết
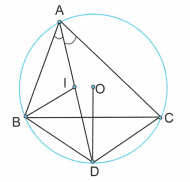
Ta luôn có DB=DC do AD là tia phân giác trong góc A. Ta sẽ chứng minh tam giác DIB cân tại D.
Thật vậy ta có: .
Mặt khác (góc nội tiếp chắn cung CD).
Mà (tính chất phân giác) suy ra .
Nhưng (tính chất góc ngoài của ). Suy ra .
Vậy tam giác BID cân tại D, suy ra .
Nhận xét
Thông qua bài toán này ta có thêm tính chất: Tâm đường tròn ngoại tiếp tam giác IBC là giao điểm của phân giác trong góc A với (O).
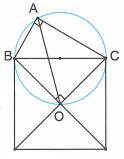
Lời giải
Vì O là tâm của hình vuông nên .
Lại có suy ra bốn điểm cùng nằm trên đường tròn đường kính BC.
Đối với đường tròn này ta thấy (góc nội tiếp cùng chắn ).
Mà .
Do , nên .
Vậy , nghĩa là AO là tia phân giác của góc vuông (đpcm).