Câu hỏi:
13/07/2024 434
Cho tam giác ABC vuông tại A (AB> AC) , đường cao AH. Trên đoạn HC lấy điểm D sao cho DH= DB vẽ CE vuông góc với
Chứng minh tứ giác AHEC nội tiếp, xác định tâm O của đường tròn ngoại tiếp tứ giác AHEC
Cho tam giác ABC vuông tại A (AB> AC) , đường cao AH. Trên đoạn HC lấy điểm D sao cho DH= DB vẽ CE vuông góc với
Chứng minh tứ giác AHEC nội tiếp, xác định tâm O của đường tròn ngoại tiếp tứ giác AHEC
Quảng cáo
Trả lời:
Giải bởi Vietjack
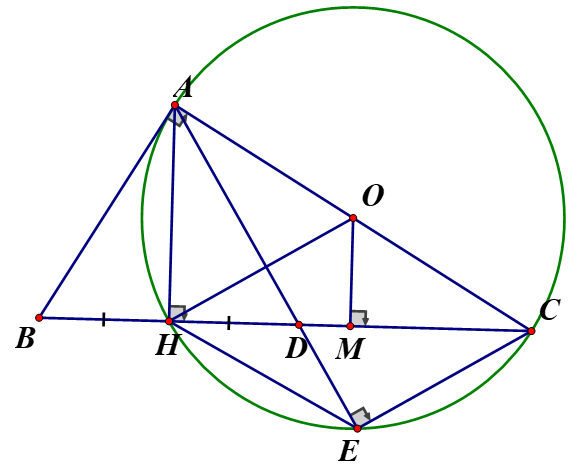
Ta có: (vì và (vì
Xét tứ giác AHCE có E, H là hai đỉnh kề nhau cùng nhìn cạnh AC dưới một góc
Suy ra tứ giác AHCE là tứ giác nội tiếp . Tâm O của đường tròn ngoại tiếp tứ giác AHCE là trung điểm của cạnh AC.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Hai đội công nhân cùng làm một công việc thì xong trong 4 giờ. Nếu mỗi đội làm riêng xong được công việc ấy, thì đội thứ hai cần nhiều hơn đội thứ nhất là 6 giờ. Hỏi mỗi đội làm riêng xong công việc ấy trong bao lâu ?
Hai đội công nhân cùng làm một công việc thì xong trong 4 giờ. Nếu mỗi đội làm riêng xong được công việc ấy, thì đội thứ hai cần nhiều hơn đội thứ nhất là 6 giờ. Hỏi mỗi đội làm riêng xong công việc ấy trong bao lâu ?
Xem đáp án »
13/07/2024
5,388
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận