Cho tam giác ABC có ba góc nhọn AB< AC nội tiếp đường tròn (O). Hai đường cao BE và CF của tam giác ABC cắt nhau tại H

a, Chứng minh bốn điểm B, C, E, F cùng thuộc một đường tròn

Xem lời giải

Câu hỏi trong đề: Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1) !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

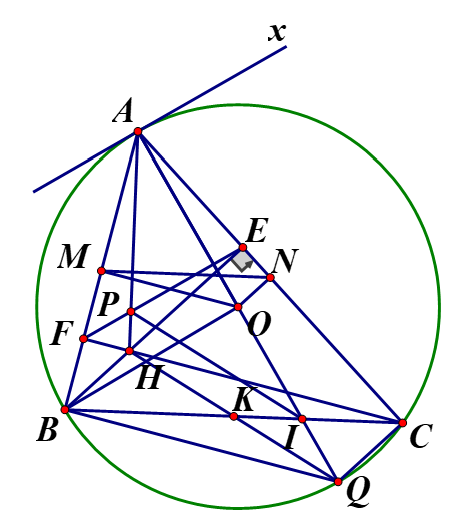
Cho tam giác ABC có ba góc nhọn AB< AC nội tiếp đường tròn (O (ảnh 1)

Ta có $\hat{B E C} = \hat{B F C} = 90^{0} (g t) \Rightarrow$ Tứ giác BFEC là tứ giác nội tiếp (tứ giác có 2 đỉnh kề nhau cùng nhìn một cạnh dưới các góc bằng nhau).

Vậy bốn điểm B, C, E,F cùng thuộc một đường tròn.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

c,Tìm tất cả các giá trị nguyên của x để biểu thức P = AB đạt giá trị nguyên lớn nhất

Xem đáp án

Lời giải

c, Điều kiện $x \geq 0, x \neq 25$

Ta có: $P = A B = \frac{4 (\sqrt{x} + 1)}{25 - x} . \frac{1}{\sqrt{x} + 1} = \frac{4}{25 - x}$

$x \in ℤ \Rightarrow P \in ℤ \Leftrightarrow \frac{4}{25 - x} \in ℤ \Rightarrow 4 ⋮ (25 - x) \Rightarrow (25 - x) \in U (4)$

Mà Ư(4)= $\{\pm 1; \pm 2; \pm 4\} \Rightarrow (25 - x) \in \{\pm 1; \pm 2; \pm 4\}$

Ta có bảng giá trị

$25 - x$	-4	-2	-1	1	2	4
x	29 ™	27™	26™	24 ™	23 ™	1™
P	-1	-2	-4	4	2	1

$\Rightarrow x \in \{23; 24; 26; 27; 29\}$ thì $P \in ℤ$

Qua bảng giá trị ta thấy với x= 24 thì P=4 là số nguyên lớn nhất

Vậy x= 24 thỏa mãn điều kiện bài toán.

Câu 2

b, Một bồn nước inox có dạng một hình trụ với chiều cao 1,75m và diện tích đáy là $0,32 m^{2} .$ Hỏi bồn nước này đựng đầy nước được bao nhiêu mét khối (Bỏ qua bề dày của bồn nước)

Xem đáp án

Lời giải

b,Thể tích bồn nước là: $V = S h = 0,32.1,75 = 0,56 (m^{3})$

Vậy bồn nước đựng được $0,56 m^{3}$ nước

Câu 3