Cho 2 số thực x≥1,y≥0 thỏa mãn điều kiện maxx2+1;2x−y+1=x+y2x2+y2 . Hỏi biểu thức P=3x+1x2+2y+1 có tất cả bao nhiêu ước số nguyên dương? A. 5 B. 6 C. 7 D. 8

Ta có một tính chất cơ bản của hàm trị tuyệt đối a+b2+a−b2=maxa;b Áp dụng ta có maxx2+1;2x−y+1=x2+2x−y+22+x2−2x+y2 Sử dụng bất đẳng thức trị tuyệt đối ta có x2+2x−y+22+x2−2x+y2≥2x2+22=2x2+22≥2x≥1 Mặt khác theo bất đẳng thức Cauchy – Schwarz ta có x+y2x2+y2≤2x2+y22x2+y2=2 Vậy VT≥2≥VP . Dấu “=” xảy ta khi và chỉ khi x=y=1 . Khi đó P=24 có tất cả 8 ước số nguyên dương.

Câu hỏi:

31/10/2022 246

Cho 2 số thực $x \geq 1, y \geq 0$ thỏa mãn điều kiện $\max \{|x^{2} + 1|; |2 x - y + 1|\} = \frac{{(x + y)}^{2}}{x^{2} + y^{2}}$ .

Hỏi biểu thức $P = 3 (x + 1) (x^{2} + 2 y + 1)$ có tất cả bao nhiêu ước số nguyên dương?

A. 5

B. 6

C. 7

D. 8

Xem lời giải

Câu hỏi trong đề: 180 câu Trắc nghiệm Toán 10 Bài 2: Hàm số và phương trình bậc 2 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có một tính chất cơ bản của hàm trị tuyệt đối $|\frac{a + b}{2}| + |\frac{a - b}{2}| = \max \{|a|; |b|\}$

Áp dụng ta có $\max \{|x^{2} + 1|; |2 x - y + 1|\} = |\frac{x^{2} + 2 x - y + 2}{2}| + |\frac{x^{2} - 2 x + y}{2}|$

Sử dụng bất đẳng thức trị tuyệt đối ta có $|\frac{x^{2} + 2 x - y + 2}{2}| + |\frac{x^{2} - 2 x + y}{2}| \geq |\frac{2 x^{2} + 2}{2}| = \frac{2 x^{2} + 2}{2} \geq 2 (x \geq 1)$

Mặt khác theo bất đẳng thức Cauchy – Schwarz ta có $\frac{{(x + y)}^{2}}{x^{2} + y^{2}} \leq \frac{{(\sqrt{2 (x^{2} + y^{2})})}^{2}}{x^{2} + y^{2}} = 2$

Vậy $V T \geq 2 \geq V P$ . Dấu “=” xảy ta khi và chỉ khi $x = y = 1$ .

Khi đó $P = 24$ có tất cả 8 ước số nguyên dương.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một chiếc cổng như hình vẽ, trong đó CD=6m , AD=4m , phía trên cổng có dạng hình parabol

Người ta cần thiết kế cổng sao cho những chiến xe container chở hàng với bề ngang thùng xe là 4m, chiều cao là 5,2mcó thể đi qua được (chiều cao được tính từ mặt đường đến nóc thùng xe và thùng xe có dạng hình hộp chữ nhật). Hỏi đỉnh I của parabol (theo mép dưới của cổng) cách mặt đất tối thiểu là bao nhiêu ?

A. 6,13m

B. 6,14m

C. 6,15m

D. 6,16m

Lời giải

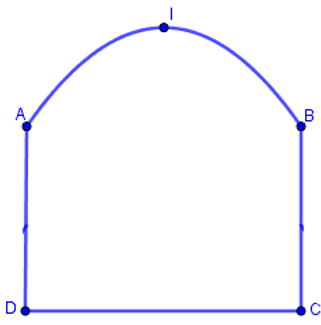
Gọi O là trung điểm của AB, K là điểm thuộc đoạn thẳng OA sao cho OK=2m .

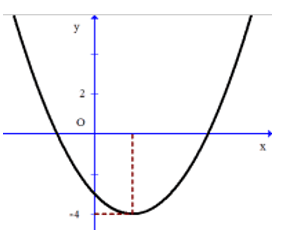
Chọn hệ tọa độ như hình vẽ. Khi đó phương trình của đường cong parabol có dạng $y = a x^{2} + c$ .

Theo giả thiết ta có parabol đi qua (-2,1,2), ( -3,0)nên ta có:

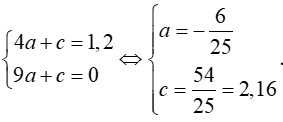
Một chiếc cổng như hình vẽ, trong đó CD=6m , AD=4m , phía trên cổng có dạng hình parabol (ảnh 2)

Vậy đỉnh Icủa parabol (theo mép dưới của cổng) cách mặt đất tối thiểu là 6,16m

Câu 2

Một vật chuyển động trong 3giờ với vận tốc v(km/h) phụ thuộc vào thời gian t(h) có đồ thị của hàm số vận tốc như hình dưới. Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh $I (2; 9)$ và trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính vận tốc v của vật tại thời điểm t=3.

A. $v = \frac{121}{4}$

B. $v = \frac{31}{4}$

C. $v = \frac{89}{4}$

D. $v = \frac{61}{4}$

Lời giải

Giả sử $v (t) = a t^{2} + b t + c (t \geq 0)$

Ta có :

$\{\begin{matrix} v (0) = c = 4 \\ v (2) = 4 a + 2 b + c = 9 \\ - \frac{b}{2 a} = 2 \end{matrix} \Leftrightarrow \{\begin{matrix} 4 a + 2 b = 5 \\ 4 a + b = 0 \\ c = 4 \end{matrix} \Leftrightarrow \{\begin{matrix} a = - \frac{5}{4} \\ b = 5 \\ c = 4 \end{matrix}$

$\Rightarrow v (t) = - \frac{5}{4} t^{2} + 5 t + 4$

Vậy $t = 3 \Rightarrow v_{0} (t) = \frac{31}{4}$

Chọn B

Câu 3

Cho hàm số: $y = f (x) = m x^{2} - 2 x - m - 1 (C)$

Với giá trị nào của m thì giá trị lớn nhất của hàm số (C) đạt giá trị nhỏ nhất.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tìm các giá trị của tham số m để cho giá trị nhỏ nhất của hàm số $y = f (x) = x^{2} + (2 m + 1) x + m^{2} - 1$ Trên đoạn $[0; 1]$ bằng 1.

A. m=1

B. $m = \sqrt{2}$

C. $[\begin{array}{l} m = \sqrt{2} \\ m = - 2 \end{array}$

D. $[\begin{array}{l} m = - \sqrt{2} \\ m = 2 \end{array}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hàm số bậc hai $y = f (x) = a x^{2} + b x + c, (a \neq 0)$ có đồ thị như hình vẽ dưới.

Tìm m để phương trình $|f (x + 2018 m) + m| = 2 m$ có 4 nghiệm thực phân biệt?

A. $0 < m < 4$

B. $0 < m < \frac{4}{3}$

C. $m < \frac{4}{3}$

D. $0 < m < 2$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số $f (x) = \sqrt{x + 2 m - 1} + \sqrt{4 - 2 m - \frac{x}{2}}$ xác địnhvới mọi $x \in [0; 2]$ khi $m \in [a; b]$ .

Giá trị $a + b = ?$

A. 2

B. 3

C. 4

D. 5

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho Parabol $(P) : y = \frac{1}{2} x^{2}$ và đường thẳng $(d) : y = (m + 1) x - m^{2} - \frac{1}{2}$ ( m là tham số). Có bao nhiêu giá trị nguyên dương của m thì đường thẳng (d) cắt Parabol (P) tại hai điểm $A (x_{1}; y_{1}), B (x_{2}; y_{2})$ sao cho biểu thức $T = y_{1} + y_{2} - x_{1} x_{2} - (x_{1} + x_{2})$ đạt giá trị nhỏ nhất.

A. 1

B. 2

C. 3

D. 4

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho 2 số thực x≥1,y≥0 thỏa mãn điều kiện maxx2+1;2x−y+1=x+y2x2+y2 . Hỏi biểu thức P=3x+1x2+2y+1 có tất cả bao nhiêu ước số nguyên dương?

Cho hàm số: y=fx=mx2−2x−m−1 C Với giá trị nào của m thì giá trị lớn nhất của hàm số (C) đạt giá trị nhỏ nhất.

Tìm các giá trị của tham số m để cho giá trị nhỏ nhất của hàm số y=fx=x2+2m+1x+m2−1 Trên đoạn 0;1 bằng 1.

Cho hàm số bậc hai y=fx=ax2+bx+c, a≠0 có đồ thị như hình vẽ dưới. Tìm m để phương trình fx+2018m+m=2m có 4 nghiệm thực phân biệt?

Cho hàm số f(x)=x+2m−1+4−2m−x2 xác địnhvới mọi x∈0;2 khi m∈a;b . Giá trị a+b=?

Cho Parabol (P):y=12x2 và đường thẳng (d):y=m+1x−m2−12 ( m là tham số). Có bao nhiêu giá trị nguyên dương của m thì đường thẳng (d) cắt Parabol (P) tại hai điểm A(x1;y1),B(x2;y2) sao cho biểu thức T=y1+y2−x1x2−(x1+x2) đạt giá trị nhỏ nhất.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho 2 số thực $x \geq 1, y \geq 0$ thỏa mãn điều kiện $\max \{|x^{2} + 1|; |2 x - y + 1|\} = \frac{{(x + y)}^{2}}{x^{2} + y^{2}}$ .

Hỏi biểu thức $P = 3 (x + 1) (x^{2} + 2 y + 1)$ có tất cả bao nhiêu ước số nguyên dương?

Cho hàm số: $y = f (x) = m x^{2} - 2 x - m - 1 (C)$

Với giá trị nào của m thì giá trị lớn nhất của hàm số (C) đạt giá trị nhỏ nhất.

Tìm các giá trị của tham số m để cho giá trị nhỏ nhất của hàm số $y = f (x) = x^{2} + (2 m + 1) x + m^{2} - 1$ Trên đoạn $[0; 1]$ bằng 1.

Cho hàm số bậc hai $y = f (x) = a x^{2} + b x + c, (a \neq 0)$ có đồ thị như hình vẽ dưới.

Tìm m để phương trình $|f (x + 2018 m) + m| = 2 m$ có 4 nghiệm thực phân biệt?

Cho hàm số $f (x) = \sqrt{x + 2 m - 1} + \sqrt{4 - 2 m - \frac{x}{2}}$ xác địnhvới mọi $x \in [0; 2]$ khi $m \in [a; b]$ .

Giá trị $a + b = ?$