Cho tam giác ABC. Chứng minh rằng nếu đường cao AH cũng là đường phân giác thì tam giác ABC cân tại A.
Quảng cáo
Trả lời:
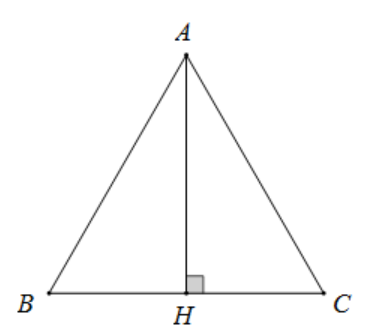
AH là đường cao của tam giác ABC nên .
AH là đường phân giác nên .
Xét tam giác AHB và tam giác AHC.
.
.
Cạnh chung AH.
Vậy tam giác AHB bằng tam giác AHC theo trường hợp g.c.g. Suy ra AB = AC hay tam giác ABC cân tại A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
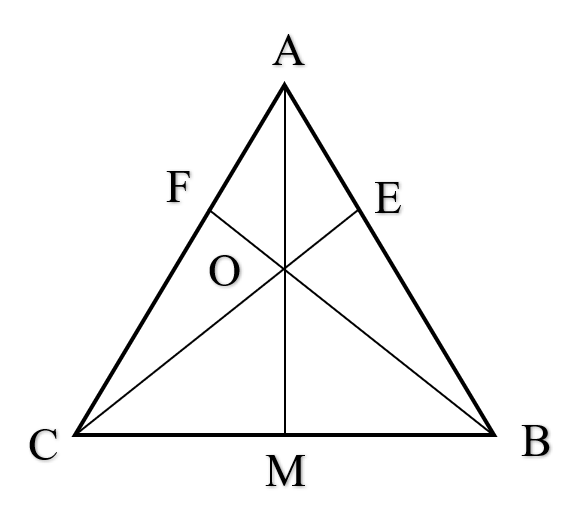
Kéo dài AO cắt BC tại M.
Xét tam giác ACE và tam giác ABF.
AC = AB ( do tam giác ABC cân tại A)
AE = AF (gt)
Góc A chung
Vậy tam giác ACE bằng tam giác ABF theo trường hợp c.g.c. Suy ra CE = BF.
Xét tam giác ECB và tam giác FBC
( do tam giác ABC cân tại A)
CE = BF
Cạnh chung BC
Vậy tam giác ECB bằng tam giác FBC theo trường hơpk c.g.c. Suy ra hay nên tam giác OBC cân tại O. Ta có OB = OC hay O nằm trên đường trung trực của BC (1).
AB = AC ( do tam giác ABC cân tại A) nên A nằm trên đường trung trực của BC. (2)
Từ (1) và (2) suy ra AO là đường trung trực của BC.
Lời giải
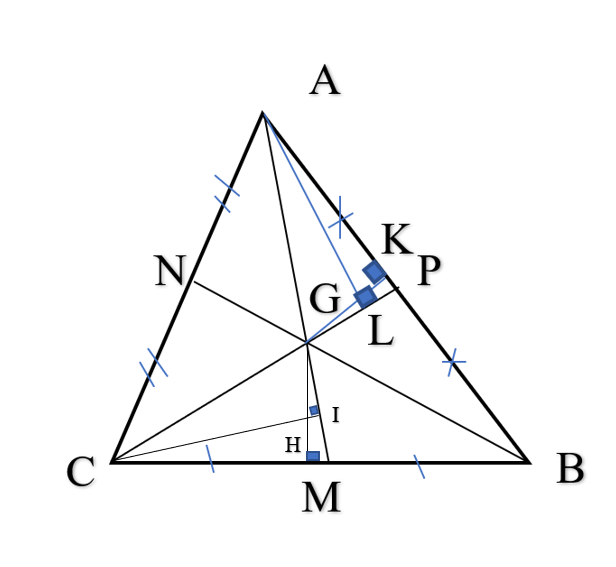
Từ G hạ đường vuông góc GK xuống AB.
Do PA = PB nên 2S∆APG = AP.GK = BP.GK = 2S∆BGP.
Từ A hạ đường vuông góc AL xuống CP.
Do GC = 2 GP nên 2S∆AGP = PG. AL = GC.AL = 2S∆AGC.
Vậy 2S∆APG = 2S∆BGP = S∆AGC.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.