Cho kiểu gen AaBb. Giả sử quá trình giảm phân tạo giao tử bình thường và không xảy ra đột biến. Sơ đồ hình cây biểu thị sự hình thành giao tử được biểu diễn như hình bên.

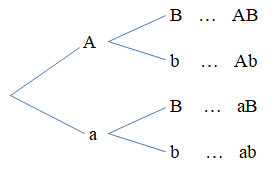
Từ sơ đồ cây, số loại giao tử của kiểu gen AaBb là:

Hướng dẫn giải

Đáp án đúng là: C

Ta loại phương án D vì không có dạng x² + y² – 2ax – 2by + c = 0.

Xét phương án A: x² + y² + 2x – 4y + 9 = 0 có a = –1, b = 2 và c = 9.

Do đó a² + b² – c = (–1)² + 2² – 9 = –4 < 0 nên loại A.

Xét phương án B: x² + y² – 6x + 4y + 13 = 0 có a = 3; b = –2 và c = 13

Do đó a² + b² – c = 3² + (–2)² – 13 = 0 nên loại B.

Xét phương án C: 2x² + 2y² – 8x – 4y + 2 = 0

Û x² + y² – 4x – 2y + 1 = 0.

Có a = 2; b = 1 và c = 1.

Do đó a² + b² – c = 2² + 1² – 1 = 4 > 0 nên chọn C.

Vậy ta chọn phương án C.

Hướng dẫn giải

Đáp án đúng là: C

Cho tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0), ta có:

⦁ Nếu ∆ < 0 thì f(x) cùng dấu với a với mọi giá trị x.

Do đó phương án B, D đều sai.

⦁ Nếu ∆ = 0 và \({x_0} = - \frac{b}{{2a}}\) là nghiệm kép của f(x) thì f(x) cùng dấu với a với mọi x ≠ x₀.

Do đó phương án C đúng.

⦁ Nếu ∆ > 0 và x₁, x₂ là hai nghiệm của f(x) (x₁ < x₂) thì f(x) trái dấu với a với mọi x trong khoảng (x₁; x₂); f(x) cùng dấu với a với mọi x thuộc hai khoảng (–∞; x₁); (x₂; +∞).

Do đó phương án A sai.

Vậy ta chọn phương án C.