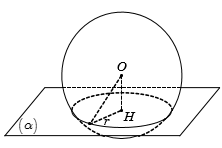
Tìm tập các tâm I của mặt cầu (S) tiếp xúc với hai mặt phẳng
Tìm tập các tâm I của mặt cầu (S) tiếp xúc với hai mặt phẳng
Quảng cáo
Trả lời:
Chọn A
Gọi A(-4,0,0) và B(6,0,0) lần lượt là giao điểm của trục x’Ox với (P) và (Q). Trung điểm E(1,0,0) của AB cách đều (P) và (Q).
Tâm I cách đều (P) và (Q) => EI nằm trong mặt (R) qua E song song và cách đều (P) và (Q) ((P)//(Q)).
VậyHot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
(S) có tâm I(2,1,-3), bán kính
Lời giải
Chọn B
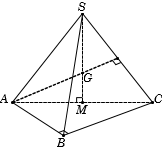
Gọi M là trung điểm AC, suy ra
Tam giác SAC có SM là đường cao và cũng là trung tuyến nên tam giác SAC cân tại S.
Ta có , suy ra tam giác SAC đều.Gọi G là trọng tâm , suy ra (1)
Tam giác ABC vuông tại B, có M là trung điểm cạnh huyền AC nên M là tâm đường tròn ngoại tiếp tam giác ABC.
Lại có nên SM là trục của tam giác ABC.
Mà G thuộc SM nên suy ra (2)
Từ (1) và (2) , suy ra hay G là tâm mặt cầu ngoại tiếp khối chóp S.ABC .
Bán kính mặt cầuLời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.