Câu hỏi:
30/01/2023 8,644
Cô dâu và chú rể mời 6 người ra chụp ảnh kỉ niệm, người thợ chụp hình có bao nhiêu cách sắp xếp sao cho cô dâu, chú rể đứng cạnh nhau.
Câu hỏi trong đề: Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án B
Phương pháp:
Sử dụng phương pháp buộc, coi cô dâu, chú rể là 1 người.
Cách giải:
Coi cô dâu, chú rể là 1 người, có \(2! = 2\) cách hoán đổi vị trí cô dâu và chú rể.
Sắp xếp 6 người được mời với 1 cặp cô dâu, chú rể có \(7!\) cách.
Suy ra có tất cả \(2.7!\) cách.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án D
Phương pháp:
Ba mặt phẳng phân biệt đôi một cắt nhau thì các giao tuyến của chúng hoặc song song hoặc đồng quy.
Cách giải:
\(\left. \begin{array}{l}\left( \alpha \right) \cap \left( \beta \right) = {d_1}\\\left( \beta \right) \cap \left( \gamma \right) = {d_2}\\\left( \gamma \right) \cap \left( \alpha \right) = {d_3}\end{array} \right\} \Rightarrow \left[ \begin{array}{l}{d_1}\parallel {d_2}\parallel {d_3}\\{d_1},{d_2},{d_3}\,\,dong\,\,quy\end{array} \right.\)
Lời giải
Phương pháp:
a) Xác định các điểm chung của hai mặt phẳng.
b) Chứng minh EF song song với một đường thẳng nằm trong mặt phẳng \(\left( {ABCD} \right)\) và \(\left( {SBC} \right)\).
c) Tìm giao điểm của SB với một đường thẳng nằm trong \(\left( {CDE} \right)\) và tìm giao điểm cả SC với một đường thẳng nằm trong \(\left( {EFM} \right).\) Từ đó suy ra thiết diện.
d) Sử dụng công thức: \(\frac{{{S_{KMN}}}}{{{S_{KEF}}}} = \frac{{KM}}{{KE}}.\frac{{KN}}{{KF}}.\)
Cách giải:
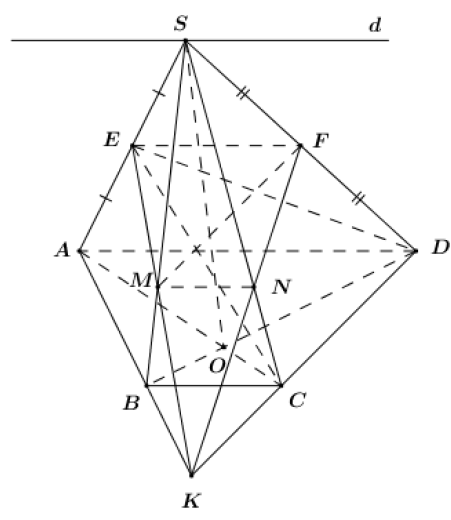
a) * Tìm \(\left( {SAC} \right) \cap \left( {SBD} \right) = ?\)
+ Dễ thấy S là điểm chung thứ nhất.
+ Trong \(\left( {ABCD} \right)\), gọi \(AC \cap BD = \left\{ O \right\}\) ta có:
\(\left\{ \begin{array}{l}O \in AC \subset \left( {SAC} \right) \Rightarrow O \in \left( {SAC} \right)\\O \in BD \subset SBD \Rightarrow O \in \left( {SBD} \right)\end{array} \right. \Rightarrow O \in \left( {SAC} \right) \cap \left( {SBD} \right) \Rightarrow O\) là điểm chung thứ hai.
Vậy \(\left( {SAC} \right) \cap \left( {SBD} \right) = SO.\)
* Tìm \(\left( {SAD} \right) \cap \left( {SBC} \right) = ?.\)
+ Dễ thấy S là điểm chung thứ nhất.
+ Ta có: \[\left\{ \begin{array}{l}\left( {SAD} \right) \supset AD\\\left( {SBC} \right) \supset BC\\AD\parallel BC\left( {gt} \right)\end{array} \right. \Rightarrow \left( {SAD} \right),\left( {SBC} \right)\] cắt nhau theo giao tuyến là đường thẳng qua S và song song với AD, BC.
Trong \(\left( {SAD} \right)\) kẻ đường thẳng d qua S và \(d\parallel AD\parallel BC \Rightarrow \left( {SAD} \right) \cap \left( {SBC} \right) = d.\)
b) Ta có: EF là đường trung bình của \(\Delta SAD\) nên \(EF\parallel AD\) (Tính chất đường trung bình của tam giác).
Mà \(AD \subset \left( {ABCD} \right) \Rightarrow EF\parallel \left( {ABCD} \right).\)
Ta có: \(EF\parallel AD\), mà \(AD\parallel BC\left( {gt} \right) \Rightarrow EF\parallel BC.\)
Lại có \(BC \subset \left( {SBC} \right) \Rightarrow EF\parallel \left( {SBC} \right).\)
c) Trong \(\left( {SAB} \right)\) gọi \(M = EK \cap SB\) ta có: \(\left\{ \begin{array}{l}M \in SB\\M \in EK \subset \left( {CDE} \right) \Rightarrow M \in \left( {CDE} \right)\end{array} \right. \Rightarrow M = SB \cap \left( {CDE} \right).\)
Trong \(\left( {SCD} \right)\) gọi \(N = FK \cap SC\) ta có: \(\left\{ \begin{array}{l}N \in SC\\N \in FK \subset \left( {EFM} \right) \Rightarrow M \in \left( {EFM} \right)\end{array} \right. \Rightarrow N = SC \cap \left( {EFM} \right).\)
Ta có: \(\left\{ \begin{array}{l}\left( {KEF} \right) \cap \left( {SAB} \right) = EM\\\left( {KEF} \right) \cap \left( {SBC} \right) = MN\\\left( {KEF} \right) \cap \left( {SCD} \right) = NF\\\left( {KEF} \right) \cap \left( {SAD} \right) = EF\end{array} \right. \Rightarrow \) Thiết diện của hình chóp cắt bởi mặt phẳng \(\left( {KEF} \right)\) là tứ giác EMNF.
d) Áp dụng định lí Menelaus cho tam giác FKD ta có: \(\frac{{CD}}{{CK}}.\frac{{NK}}{{NF}}.\frac{{SF}}{{SD}} = 1.\)
Áp dụng định lí Ta-lét ta có: \(\frac{{KC}}{{KD}} = \frac{{BC}}{{AD}} = \frac{1}{2} \Rightarrow C\) là trung điểm của \(KD \Rightarrow \frac{{CK}}{{CD}} = 1.\)
F là trung điểm của \(SD\left( {gt} \right) \Rightarrow \frac{{SF}}{{SD}} = \frac{1}{2}.\)
\( \Rightarrow 1.\frac{{NK}}{{NF}}.\frac{1}{2} = 1 \Rightarrow \frac{{NK}}{{NF}} = 2.\)
Tương tự ta có: \(\frac{{MK}}{{ME}} = 2.\)
Suy ra \(\frac{{{S_{KMN}}}}{{{S_{KEF}}}} = \frac{{KM}}{{KE}}.\frac{{KN}}{{KF}} = \frac{2}{3}.\frac{2}{3} = \frac{4}{9}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
-
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
-
Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)
-
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
-
38 câu trắc nghiệm Toán 11 Kết nối tri thức Lôgarit có đáp án
-
33 câu trắc nghiệm Toán 11 Kết nối tri thức Bài 29: Công thức cộng xác suất có đáp án
-
10 Bài tập Biểu diễn góc lượng giác trên đường tròn lượng giác (có lời giải)