Câu hỏi:
13/07/2024 375
Cho hình hộp \(ABCD.A'B'C'D'\). Lấy E, F lần lượt là trung điểm các cạnh AB, \(CC'\) và O là tâm của đáy \(A'B'C'D'\). Gọi I là giao điểm của BC và mặt phẳng \(\left( {FOE} \right)\). Tính tỉ số \(\frac{{IC}}{{IB}}\) và xác định thiết diện của hình hộp cắt bởi mặt phẳng \(\left( {FOE} \right)\).
Câu hỏi trong đề:
Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa... kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 70k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phương pháp:
Gọi N là trung điểm của \(A'B'\), G là giao điểm của \(NC'\) với EF.
Từ đó mở rộng mặt phẳng \(\left( {FOE} \right)\) rồi tìm giao tuyến của \(\left( {FOE} \right)\) với các mặt của hình hộp.
Cách giải:
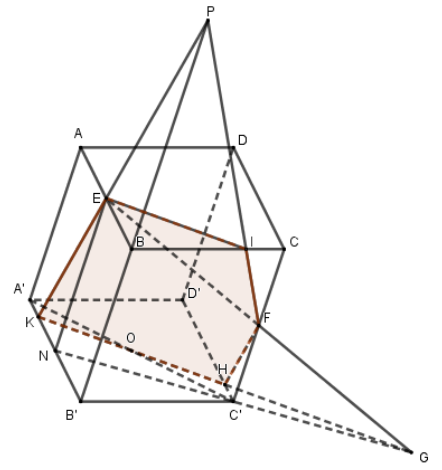
Gọi N là trung điểm của \(A'B' \Rightarrow NE//FC'\) nên bốn điểm N, E, F, C đồng phẳng.
Trong \(\left( {NEFC} \right)\), gọi \(G = NC' \cap EF \Rightarrow G \in EF \subset \left( {FOE} \right)\).
Trong \(\left( {A'B'C'D'} \right)\), gọi H, K lần lượt là giao điểm của GO với \(D'C'\), \(A'B'\)
Khi đó \(\left( {FOE} \right) \equiv \left( {GKE} \right)\).
Trong \(\left( {ABB'A'} \right)\), gọi \(P = KE \cap B'B \Rightarrow P \in BB' \subset \left( {BCC'B'} \right)\).
Trong \(\left( {BCC'B'} \right)\), gọi \(I = PF \cap BC \Rightarrow \left\{ \begin{array}{l}I \in BC\\I \in PF \subset \left( {GKE} \right) \equiv \left( {FOE} \right)\end{array} \right. \Rightarrow I = BC \cap \left( {FOE} \right)\).
Khi đó
\(\left( {FOE} \right) \cap \left( {A'B'C'D'} \right) = HK\)
\(\left( {FOE} \right) \cap \left( {ABB'A'} \right) = KE\)
\(\left( {FOE} \right) \cap \left( {ABCD} \right) = EI\)
\(\left( {FOE} \right) \cap \left( {BCC'B'} \right) = IF\)
\(\left( {FOE} \right) \cap \left( {DCC'D'} \right) = FH\)
Thiết diện là ngũ giác EIFHK.
Ta có, \(\frac{{IB}}{{IC}} = \frac{{PB}}{{CF}}\), \(CF = \frac{1}{2}CC' \Rightarrow \frac{{PB}}{{CF}} = \frac{{PB}}{{\frac{1}{2}CC'}} = 2.\frac{{PB}}{{BB'}}\) .
\(HC'//KN \Rightarrow \frac{{HC'}}{{KN}} = \frac{{GC'}}{{GN}}\)
Mà \(C'F//NE \Rightarrow \frac{{GC'}}{{GN}} = \frac{{C'F}}{{NE}} = \frac{1}{2} \Rightarrow \frac{{HC'}}{{KN}} = \frac{1}{2} \Rightarrow \frac{{A'K}}{{KN}} = \frac{1}{2} \Rightarrow \frac{{A'K}}{{A'N}} = \frac{1}{3} \Rightarrow \frac{{A'K}}{{A'B'}} = \frac{1}{6}\)
\( \Rightarrow \frac{{KN}}{{A'N}} = \frac{2}{3} = \frac{{K'N}}{{NB'}} \Rightarrow \frac{{K'N}}{{NB'}} = \frac{2}{5} \Rightarrow \frac{{NE}}{{PB'}} = \frac{2}{5} \Rightarrow \frac{{BB'}}{{PB'}} = \frac{2}{5} \Rightarrow \frac{{PB}}{{PB'}} = \frac{3}{5} \Rightarrow \frac{{PB}}{{BB'}} = \frac{3}{2}\)
Vậy \(\frac{{IB}}{{IC}} = \frac{{PB}}{{CF}} = 2.\frac{{PB}}{{BB'}} = 2.\frac{3}{2} = 3\).
Nhà sách VIETJACK:
Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8
Đã bán 211
₫ 119.000
₫ 45.000
Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025
Đã bán 244
₫ 136.000
₫ 58.000
Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack
Đã bán 1k
₫ 104.000
₫ 52.000
Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack
Đã bán 218
₫ 130.000
₫ 75.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = \frac{{{n^2} + 3}}{{2{n^2} - 1}}\) với \(n \in {\mathbb{N}^*}\). Tìm số hạng \({u_5}\).
Xem đáp án »
02/02/2023
13,787
Câu 3:
Cho hai đường thẳng phân biệt a, b và mặt phẳng \(\left( \alpha \right)\). Giả sử \(a//\left( \alpha \right)\), \(b \subset \left( \alpha \right)\). Khi đó:
Xem đáp án »
02/02/2023
6,432
Câu 4:
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD với O là giao điểm hai đường chéo AC và BD. Gọi M, N lần lượt là trung điểm các cạnh SA và SD.
1. Chứng minh MO song song với mặt phẳng \(\left( {SBC} \right)\) và mặt phẳng \(\left( {OMN} \right)\) song song với mặt phẳng \(\left( {SBC} \right)\).
2. Gọi K là trung điểm của MO. Chứng minh rằng NK song song với \(\left( {SBC} \right)\).
3. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng \(\left( {OMN} \right)\). Hỏi thiết diện là hình gì?
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD với O là giao điểm hai đường chéo AC và BD. Gọi M, N lần lượt là trung điểm các cạnh SA và SD.
1. Chứng minh MO song song với mặt phẳng \(\left( {SBC} \right)\) và mặt phẳng \(\left( {OMN} \right)\) song song với mặt phẳng \(\left( {SBC} \right)\).
2. Gọi K là trung điểm của MO. Chứng minh rằng NK song song với \(\left( {SBC} \right)\).
3. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng \(\left( {OMN} \right)\). Hỏi thiết diện là hình gì?
Xem đáp án »
13/07/2024
5,571
Câu 5:
Gieo một con xúc xắc cân đối đồng chất 2 lần. Tính xác suất để tổng số chấm xuất hiện trong hai lần gieo bằng 8.
Xem đáp án »
02/02/2023
4,673
Câu 6:
Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \(\left\{ \begin{array}{l}{u_1} = - 3\\{u_n} = \frac{1}{2}{u_{n - 1}} + 1\end{array} \right.\) với \(n \in {\mathbb{N}^*}\), \(n \ge 2\). Tìm số hạng \({u_4}\).
Xem đáp án »
02/02/2023
2,161
Câu 7:
Cho hình lăng trụ \(ABC.A'B'C'\) . Gọi H là trung điểm của \(A'B'\). Hỏi đường thẳng \(B'C\) song song với mặt phẳng nào sau đây?
Xem đáp án »
02/02/2023
1,635
🔥 Đề thi HOT:
-
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
10 Bài tập Biến cố hợp. Biến cố giao (có lời giải)
-
38 câu trắc nghiệm Toán 11 Kết nối tri thức Lôgarit có đáp án
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
-
10 Bài tập Bài toán thực tiễn liên quan đến thể tích (có lời giải)
-
100 câu trắc nghiệm Đạo hàm cơ bản (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận