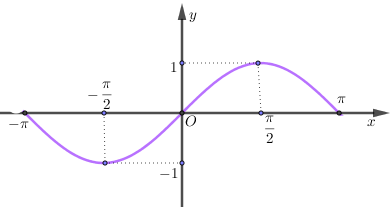
Cho hình lập phương \(ABCD.A'B'C'D'\), khoảng cách từ \(C'\) đến mặt phẳng \(\left( {A'BD} \right)\) bằng \(\frac{{4a\sqrt 3 }}{3}.\) Tính theo \(a\) thể tích khối lập phương \(ABCD.A'B'C'D'\,.\)
Câu hỏi trong đề: Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án !!
Quảng cáo
Trả lời:
Lời giải
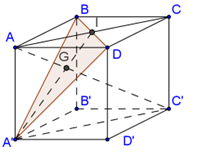
Gọi \(I\) là giao điểm của \(AC\) và \(BD.\)
Trong mặt phẳng \(\left( {ACC'A'} \right)\)\(AC'\) cắt \(A'I\) tại \(G.\)
Do \(AI\)song song \(A'C'\) và \(AI = \frac{1}{2}AC'\) nên \(IG = \frac{1}{2}GA'.\)
Suy ra \(G\) là trọng tâm tam giác \(A'BD\), mà tam giác \(A'BD\) đều (có các cạnh là các đường chéo của những hình vuông bằng nhau) nên \(GA' = GB = GD\) và \(AA' = AB = AD\) suy ra \(AG \bot (A'BD).\)
Do đó khoảng cách từ \(C'\)đến mặt phẳng \(\left( {A'BD} \right)\) là \(C'G.\)
Mặt khác \(C'G = \frac{2}{3}AC' = \frac{2}{3}AB\sqrt 3 = \frac{{4a\sqrt 3 }}{3} \Rightarrow AB = 2a.\) Vậy \(V = 8{a^3}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Câu 2
Lời giải
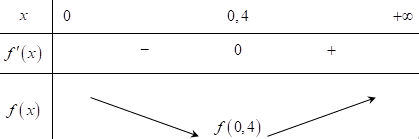
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.