Một người gửi tiền vào ngân hàng 100 triệu đồng thể thức lãi kép, kỳ hạn là 1 tháng với lãi suất 0,5% một tháng. Hỏi sau ít nhất bao nhiêu tháng, người đó có nhiều hơn 125 triệu đồng?
Một người gửi tiền vào ngân hàng 100 triệu đồng thể thức lãi kép, kỳ hạn là 1 tháng với lãi suất 0,5% một tháng. Hỏi sau ít nhất bao nhiêu tháng, người đó có nhiều hơn 125 triệu đồng?
A. 44 tháng
B. 45 tháng
C. 47 tháng
D. 46 tháng
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án B
Phương pháp:
Sử dụng công thức lãi kép \({A_n} = A{\left( {1 + r} \right)^n}\)
Cách giải:
Ta có: \({A_n} = A{\left( {1 + r} \right)^n}\)
\( \Rightarrow 100{\left( {1 + \frac{{0,5}}{{100}}} \right)^n} > 125 \Leftrightarrow n > {\log _{\left( {1 + \frac{{0,5}}{{100}}} \right)}}\frac{{125}}{{100}} \simeq 44,74\)
Vậy sau ít nhất 45 tháng.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(S = 4\)
B. \(S = 8\)
C. \(S = 2\sqrt 5 \)
D. \(S = 2\)
Lời giải
Đáp án A
Phương pháp:
+) Giải phương trình \(y' = 0\) xác định tọa độ các điểm cực trị AB.
+) Nhận xét các điểm A, B. Chứng minh tam giác OAB vuông tại O.
+) \({S_{\Delta OAB}} = \frac{1}{2}OA.OB\)
Cách giải:
Ta có: \(y' = 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 4 \Rightarrow A\left( {0;4} \right) \in Oy\\x = 2 \Rightarrow y = 0 \Rightarrow B\left( {2;0} \right) \in Ox\end{array} \right. \Rightarrow \Delta OAB\) vuông tại O.
Có \(OA = 4;\,\,OB = 2 \Rightarrow {S_{\Delta OAB}} = \frac{1}{2}OA.OB = \frac{1}{2}.4.2 = 4\)
Câu 2
A. \(D = \left( { - \infty ;1} \right)\)
B. \(D = \left[ {1; + \infty } \right)\)
C. \(D = \left( {0;1} \right)\)
D. \(D = \left( {1; + \infty } \right)\)
Lời giải
Đáp án D
Phương pháp:
Cho hàm số \(y = {x^n}\)
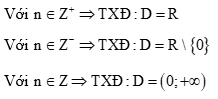
Cách giải:
\( - \frac{1}{2} \notin Z \Rightarrow \) Hàm số xác định \(x - 1 > 0 \Leftrightarrow x > 1\)
Vậy tập xác định của hàm số là \(D = \left( {1; + \infty } \right)\)
Câu 3
A. –1
B. –4
C. 4
D. 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(V = \frac{{8{a^3}}}{3}\)
B. \(V = \frac{{2{a^3}}}{3}\)
C. \(V = 2{a^3}\)
D. \(V = 4{a^3}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\left( {1;2} \right)\)
B. \(\left( {3; + \infty } \right)\)
C. \(\left( {2; + \infty } \right)\)
D. \(\left( {1; + \infty } \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Kết quả khác
B. 1
C. 0
D. 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo