Chọn phát biểu đúng trong các phát biểu sau:
Chọn phát biểu đúng trong các phát biểu sau:
A. Đồ thị hàm số logarit không nằm bên dưới trục hoành
B. Đồ thị hàm mũ với cơ số dương nhỏ hơn 1 thì nằm dưới trục hoành
C. Đồ thị hàm số logarit luôn nằm bên phải trục tung
D. Đồ thị hàm số mũ với số mũ âm luôn có hai tiệm cận.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án C
Phương pháp:
Dựa vào hình dáng đồ thị các hàm số mũ và logarit.
Cách giải:
A sai vì độ thị hàm số logarit \(y = {\log _a}x\) có thể nằm trên trục hoành.
B sai vì đồ thị hàm số mũ \(y = {a^x}\) luôn nằm trên trục hoành và nhận Ox làm tiệm cận ngang.
C đúng vì đồ thị hàm số logarit \(y = {\log _a}x\) luôn nằm bên phải trục tung và nhận Oy làm tiệm cận đứng.
D sai vì đồ thị hàm số mũ \(y = {a^x}\)luôn có một tiệm cận duy nhất là trục Ox.
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(S = 4\)
B. \(S = 8\)
C. \(S = 2\sqrt 5 \)
D. \(S = 2\)
Lời giải
Đáp án A
Phương pháp:
+) Giải phương trình \(y' = 0\) xác định tọa độ các điểm cực trị AB.
+) Nhận xét các điểm A, B. Chứng minh tam giác OAB vuông tại O.
+) \({S_{\Delta OAB}} = \frac{1}{2}OA.OB\)
Cách giải:
Ta có: \(y' = 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 4 \Rightarrow A\left( {0;4} \right) \in Oy\\x = 2 \Rightarrow y = 0 \Rightarrow B\left( {2;0} \right) \in Ox\end{array} \right. \Rightarrow \Delta OAB\) vuông tại O.
Có \(OA = 4;\,\,OB = 2 \Rightarrow {S_{\Delta OAB}} = \frac{1}{2}OA.OB = \frac{1}{2}.4.2 = 4\)
Câu 2
A. \(D = \left( { - \infty ;1} \right)\)
B. \(D = \left[ {1; + \infty } \right)\)
C. \(D = \left( {0;1} \right)\)
D. \(D = \left( {1; + \infty } \right)\)
Lời giải
Đáp án D
Phương pháp:
Cho hàm số \(y = {x^n}\)
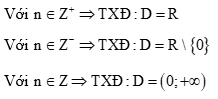
Cách giải:
\( - \frac{1}{2} \notin Z \Rightarrow \) Hàm số xác định \(x - 1 > 0 \Leftrightarrow x > 1\)
Vậy tập xác định của hàm số là \(D = \left( {1; + \infty } \right)\)
Câu 3
A. –1
B. –4
C. 4
D. 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(V = \frac{{8{a^3}}}{3}\)
B. \(V = \frac{{2{a^3}}}{3}\)
C. \(V = 2{a^3}\)
D. \(V = 4{a^3}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\left( {1;2} \right)\)
B. \(\left( {3; + \infty } \right)\)
C. \(\left( {2; + \infty } \right)\)
D. \(\left( {1; + \infty } \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Kết quả khác
B. 1
C. 0
D. 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo