Câu hỏi:
21/02/2023 239
Cho khối hộp chữ nhật ABCD.A’B’C’D’ có \(AD = 8;\,\,CD = 6;\,\,AD' = 12\). Tính diện tích toàn phần của khối trụ có hai đường tròn đáy ngoại tiếp hình chữ nhật ABCD và A’B’C’D’.
Cho khối hộp chữ nhật ABCD.A’B’C’D’ có \(AD = 8;\,\,CD = 6;\,\,AD' = 12\). Tính diện tích toàn phần của khối trụ có hai đường tròn đáy ngoại tiếp hình chữ nhật ABCD và A’B’C’D’.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án D
Phương pháp:
Diện tích toàn phần của hình trụ bán kính R, đường cao h là \({S_{tp}} = 2\pi R\left( {R + h} \right)\)
Cách giải:
Xét tam giác vuông ACD có: \(AC = \sqrt {{8^2} + {6^2}} = 10 \Rightarrow OA = 5 = R\)
Xét tam giác vuông AA’C’ có: \(AA' = \sqrt {AC{'^2} - A{C^2}} = \sqrt {{{12}^2} - {{10}^2}} = 2\sqrt {11} = h\)
Vậy Tính diện tích toàn phần của khối trụ có hai đường tròn đáy ngoại tiếp hình chữ nhật ABCD và A’B’C’D’ là: \(2\pi R\left( {h + R} \right) = 2\pi .5\left( {5 + 2\sqrt {11} } \right) = 10\pi \left( {2\sqrt {11} + 5} \right)\)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án A
Phương pháp:
+) Giải phương trình \(y' = 0\) xác định tọa độ các điểm cực trị AB.
+) Nhận xét các điểm A, B. Chứng minh tam giác OAB vuông tại O.
+) \({S_{\Delta OAB}} = \frac{1}{2}OA.OB\)
Cách giải:
Ta có: \(y' = 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 4 \Rightarrow A\left( {0;4} \right) \in Oy\\x = 2 \Rightarrow y = 0 \Rightarrow B\left( {2;0} \right) \in Ox\end{array} \right. \Rightarrow \Delta OAB\) vuông tại O.
Có \(OA = 4;\,\,OB = 2 \Rightarrow {S_{\Delta OAB}} = \frac{1}{2}OA.OB = \frac{1}{2}.4.2 = 4\)
Lời giải
Đáp án D
Phương pháp:
Cho hàm số \(y = {x^n}\)
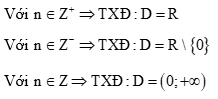
Cách giải:
\( - \frac{1}{2} \notin Z \Rightarrow \) Hàm số xác định \(x - 1 > 0 \Leftrightarrow x > 1\)
Vậy tập xác định của hàm số là \(D = \left( {1; + \infty } \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo