Cho khối chóp S.ABCD có thể tích bằng 81. Gọi M, N, P lần lượt là trọng tâm các mặt bên \(\left( {SAB} \right);\,\left( {SBC} \right);\,\left( {SCD} \right);\,\left( {SDC} \right)\). Tính thể tích V của khối chóp S.MNPQ?
Cho khối chóp S.ABCD có thể tích bằng 81. Gọi M, N, P lần lượt là trọng tâm các mặt bên \(\left( {SAB} \right);\,\left( {SBC} \right);\,\left( {SCD} \right);\,\left( {SDC} \right)\). Tính thể tích V của khối chóp S.MNPQ?
D. \(V = 54\)
Quảng cáo
Trả lời:
Đáp án C
Phương pháp:
Sử dụng công thức Simpson tính tỉ lệ thể tích, lưu ý chỉ áp dụng đối với chóp tam giác.Cách giải:

Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA.
Ta có \({S_{EFGH}} = \frac{1}{2}{S_{ABCD}} \Rightarrow {V_{S.EFGH}} = \frac{1}{2}{V_{S.ABCD}}\)
\(\frac{{{V_{S.MQN}}}}{{{V_{S.EHF}}}} = \frac{{SM}}{{SE}}.\frac{{SQ}}{{SH}}.\frac{{SN}}{{SF}} = {\left( {\frac{2}{3}} \right)^2} = \frac{8}{{27}} \Rightarrow {V_{S.MQN}} = \frac{8}{{27}}{V_{S.EFH}} = \frac{8}{{27}}.\frac{1}{2}{V_{S.EFGH}} = \frac{4}{{27}}{V_{S.EFGH}}\)
\(\frac{{{V_{S.PQN}}}}{{{V_{S.GHF}}}} = \frac{{SP}}{{SG}}.\frac{{SQ}}{{SH}}.\frac{{SN}}{{SF}} = {\left( {\frac{2}{3}} \right)^2} = \frac{8}{{27}} \Rightarrow {V_{S.PQN}} = \frac{8}{{27}}{V_{S.GFH}} = \frac{8}{{27}}.\frac{1}{2}{V_{S.EFGH}} = \frac{4}{{27}}{V_{S.EFGH}}\)
\( \Rightarrow {V_{S.MQN}} + {V_{S.PQN}} = 2.\frac{4}{{27}}{V_{S.EFGH}} = \frac{8}{{27}}{V_{EFGH}} = \frac{4}{{27}} = \frac{4}{{27}}{V_{S.ABCD}} = 12\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
D. \(S = 2\)
Lời giải
Đáp án A
Phương pháp:
+) Giải phương trình \(y' = 0\) xác định tọa độ các điểm cực trị AB.
+) Nhận xét các điểm A, B. Chứng minh tam giác OAB vuông tại O.
+) \({S_{\Delta OAB}} = \frac{1}{2}OA.OB\)
Cách giải:
Ta có: \(y' = 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 4 \Rightarrow A\left( {0;4} \right) \in Oy\\x = 2 \Rightarrow y = 0 \Rightarrow B\left( {2;0} \right) \in Ox\end{array} \right. \Rightarrow \Delta OAB\) vuông tại O.
Có \(OA = 4;\,\,OB = 2 \Rightarrow {S_{\Delta OAB}} = \frac{1}{2}OA.OB = \frac{1}{2}.4.2 = 4\)
Câu 2
D. \(D = \left( {1; + \infty } \right)\)
Lời giải
Đáp án D
Phương pháp:
Cho hàm số \(y = {x^n}\)
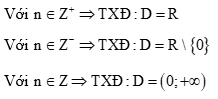
Cách giải:
\( - \frac{1}{2} \notin Z \Rightarrow \) Hàm số xác định \(x - 1 > 0 \Leftrightarrow x > 1\)
Vậy tập xác định của hàm số là \(D = \left( {1; + \infty } \right)\)
Câu 3
D. 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
D. \(V = 4{a^3}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
D. 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
D. \(\left( {1; + \infty } \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.