Cho lăng trụ đứng ABC.A’B’C’ có \(AB = AC = BB' = a,\,\,\,BAC = {120^0}\). Gọi I là trung điểm của CC’. Ta có cosin của góc giữa hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {AB'I} \right)\) bằng:
Cho lăng trụ đứng ABC.A’B’C’ có \(AB = AC = BB' = a,\,\,\,BAC = {120^0}\). Gọi I là trung điểm của CC’. Ta có cosin của góc giữa hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {AB'I} \right)\) bằng:
Quảng cáo
Trả lời:
Đáp án B
Cách giải:
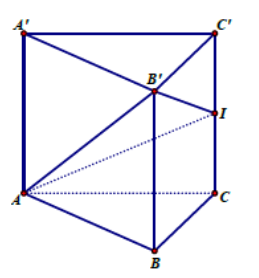
Diện tích tam giác ABC:
\({S_{ABC}} = \frac{1}{2}.AB.AC.\sin A = \frac{{\sqrt 3 {a^2}}}{4}\)
Có \(BC = \sqrt {A{B^2} + A{C^2} - 2AB.AC.{\mathop{\rm cosBAC}\nolimits} } = A\sqrt 3 \)
Ta có: \(AB' = \sqrt {{a^2} + a} = a\sqrt 2 ,\,\,\,AI = \sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 5 }}{2}\)
\(B'I = \sqrt {3{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt {13} }}{2}\)
Ta được \(AB{'^2} + A{I^2} = 2{a^2}{\left( {\frac{{a\sqrt 5 }}{2}} \right)^2} = \frac{{13{a^2}}}{4} = B'{I^2}\).
Suy ra tam giác AB’I vuông tại A, có diện tích bằng:
\({S_{AB'I}} = \frac{1}{2}.AB'.AI = \frac{1}{2}a\sqrt 2 .\frac{{a\sqrt 5 }}{2} = \frac{{{a^2}\sqrt {10} }}{4}\)
Tam giác ABC là hình chiếu vuông góc của tam giác AB’I trên ABC ABI \(\left( {ABC} \right)\) nên ta có:
\({S_{ABC}} = \cos \,\alpha .{S_{AB'I}} \Leftrightarrow \cos \alpha = \frac{{{a^2}\sqrt 3 }}{4}:\frac{{{a^2}\sqrt {10} }}{4} = \frac{{\sqrt {30} }}{{10}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
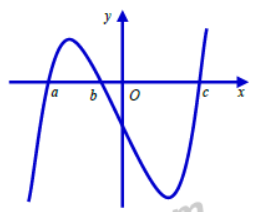
D. \(\left( {1;3} \right)\)
Lời giải
Đáp án D
Phương pháp:
Giải bất phương trình \(y' < 0\)
Cách giải:
Tập xác định \(D = R\)
\(y' = {x^3} - 4x + 3;\,\,\,y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\)
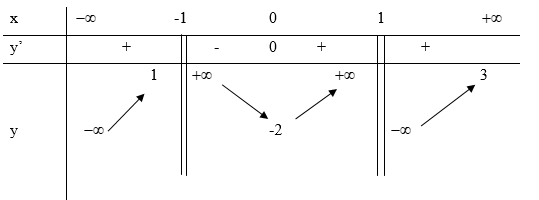
Bảng biến thiên:
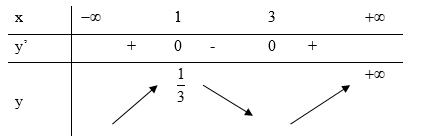
Từ bảng biến thiên, ta thấy hàm số nghịch biến trên \(\left( {1;3} \right)\)
Lời giải
Đáp án C
Phương pháp:
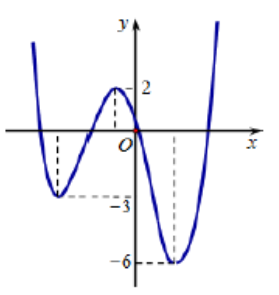
Số điểm cực trị của hàm số \(y = f\left( x \right)\) là số điểm mà qua đó \(f'\left( x \right)\) đổi dấu.
Cách giải:
\(y = f\left( x \right) - 2x \Rightarrow y' = f'\left( x \right) - 2\)
Ta có: \(y' = 0 \Leftrightarrow f'\left( x \right) - 2 = 0 \Leftrightarrow f'\left( x \right) = 2 \Leftrightarrow \left[ \begin{array}{l}x = {x_1}\\x = 0\\x = {x_2}\end{array} \right.\)
Bảng biến thiên:
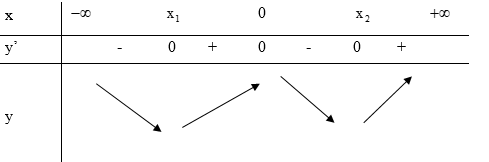
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
D. \({1^{ - \sqrt 2 }}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.