Cho số phức z và w thỏa mãn \(z + {\rm{w}} = 3 + 4i\) và \(\left| {z - {\rm{w}}} \right| = 9\). Tìm giá trị lớn nhất của biểu thức \(T = \left| z \right| + \left| {\rm{w}} \right|\)
Cho số phức z và w thỏa mãn \(z + {\rm{w}} = 3 + 4i\) và \(\left| {z - {\rm{w}}} \right| = 9\). Tìm giá trị lớn nhất của biểu thức \(T = \left| z \right| + \left| {\rm{w}} \right|\)
A. \(Max\,T = \sqrt {176} \)
B. \(Max\,T = 14\)
C. \(Max\,T = 4\)
D. \(Max\,T = \sqrt {106} \)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án D
Phương pháp:
+) Rút z theo w, tìm tập hợp các điểm biểu diễn số phức w.
+) Biểu diễn hình học tất cả các yếu tố có trong bài toán.
+) Tìm điều kiện để P đạt giá trị lớn nhất.
Cách giải:
\(z + {\rm{w}} = 3 + 4i \Rightarrow z = 3 + 4i - {\rm{w}} \Rightarrow \left| {3 + 4i - 2w} \right| = 9 \Leftrightarrow \left| {{\rm{w}} - \frac{3}{2} - 2i} \right| = \frac{9}{2}\)
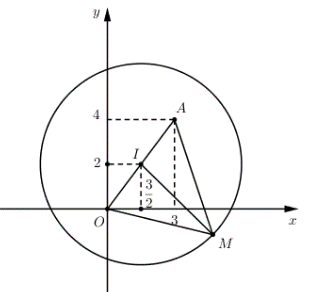
Khi đó tập hợp các điểm biểu diễn số phức w là đường tròn tâm \(I\left( {\frac{3}{2};2} \right)\) bán kính \(R = \frac{9}{2}\)
Ta có: \(T = \left| z \right| + \left| {\rm{w}} \right| = \left| {{\rm{w}} - 3 - 4i} \right| + \left| {\rm{w}} \right|\)
Gọi M là điểm biểu diễn số phức w, \(A\left( {3;4} \right)\) là điểm biểu diễn số phức \(z = 3 + 4i\). Dễ thấy I là trung điểm của OA.
Khi đó \(P = MO + MA\)
\({P_{max}} \Leftrightarrow OM = OA \Leftrightarrow MI \bot OA\)
Ta có: \(OI = \sqrt {\frac{9}{4} + 4} = \frac{5}{2},\,\,\,IM = R = \frac{9}{2}\)
\( \Rightarrow OM = \sqrt {\frac{{25}}{4} + \frac{{81}}{4}} = \frac{{\sqrt {106} }}{2}\)
\( \Rightarrow {P_{max}} = 2OM = \sqrt {106} \)
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
. Hàm số đồng biến trên khoảng \(\left( {\frac{1}{e}; + \infty } \right)\)
B. Hàm số đồng biến trên khoảng \(\left( {\frac{1}{e}; + \infty } \right)\)
C. Hàm số có đạo hàm \(y' = 1 + \ln x\)
D. Hàm số có tập xác định là \(D = \left( {0; + \infty } \right)\)
Lời giải
Đáp án A
Phương pháp:
+) Tìm TXĐ của hàm số.
+) Tính đạo hàm của hàm số.
+) Giải bất phương trình \(y' > 0\) và suy ra các khoảng đồng biến của hàm số.
Cách giải:
TXĐ: \(D = \left( {0; + \infty } \right) \Rightarrow \) D đúng
Ta có: \(y' = \ln x + x.\frac{1}{x} = \ln x + 1 \Rightarrow \) C đúng
\(y' > 0 \Leftrightarrow \ln x > - 1 \Leftrightarrow x > {e^{ - 1}} = \frac{1}{e} \Rightarrow \) Hàm số đồng biến trên khoảng \(\left( {\frac{1}{e}; + \infty } \right) \Rightarrow \) B đúng
Câu 2
A. \(x = - 2\)
B. \(y = 3\)
C. \(x = - 1\)
D. \(y = 2\)
Lời giải
Đáp án B
Phương pháp:
Đồ thị hàm số \(y = \frac{{ax + b}}{{cx + d}}\left( {ad - bc \ne 0} \right)\) có TCN \(y = \frac{a}{c}\)
Cách giải:
\(y = 1 + \frac{{2x + 1}}{{x + 2}} = \frac{{3x + 3}}{{x + 2}}\) có TCN \(y = 3\)
Câu 3
A. \(D = R\backslash \left\{ {k\pi ,\,\,k \in Z} \right\}\)
B. \(D = R\backslash \left\{ {\frac{{k\pi }}{2},\,\,k \in Z} \right\}\)
C. \(D = R\backslash \left\{ {\frac{\pi }{2} + k\pi ,\,\,k \in Z} \right\}\)
D. \(D = R\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(m \le - 1\) hoặc \(m \ge 2\)
B. \(m \le - 1\)
C. \(m \ge 2\)
D. \( - 1 \le m \le 2\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(R = \sqrt {53} \)
B. \(R = 4\sqrt 2 \)
C. \(R = \sqrt {10} \)
D. \(R = 3\sqrt 7 \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(V = \frac{{2{a^3}}}{{3\sqrt 5 }}\)
B. \(V = \frac{{{a^3}}}{{3\sqrt 5 }}\)
C. \(V = \frac{{{a^3}}}{{3\sqrt 3 }}\)
D. \(V = \frac{{{a^3}}}{{\sqrt 5 }}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\left( S \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 25\)
B. \(\left( S \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 16\)
C. \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 1} \right)^2} = 34\)
D. \(\left( S \right):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 34\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo