Câu hỏi:
22/02/2023 479
Ban đầu ta có một tam giác đều cạnh bằng 3 (hình 1). Tiếp đó ta chia mỗi cạnh của tam giác thành 3 đoạn bằng nhau và thay mỗi đoạn ở giữa bởi hai đoạn bằng nó sao cho chúng tạo với đoạn bỏ đi một tam giác đều về phía ngoài ta được hình 2. Khi quay hình 2 xung quanh trục d ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.
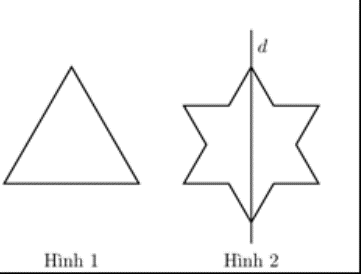
Ban đầu ta có một tam giác đều cạnh bằng 3 (hình 1). Tiếp đó ta chia mỗi cạnh của tam giác thành 3 đoạn bằng nhau và thay mỗi đoạn ở giữa bởi hai đoạn bằng nó sao cho chúng tạo với đoạn bỏ đi một tam giác đều về phía ngoài ta được hình 2. Khi quay hình 2 xung quanh trục d ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án C
Phương pháp:
Sử dụng các công thức tính thể tích khối trụ, khối nón.
Cách giải:
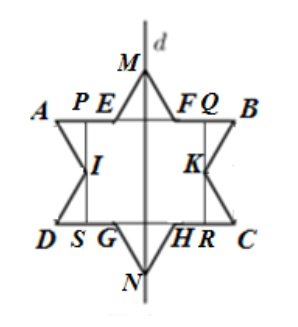
Kẻ PS, QR lần lượt qua I và K và vuông góc với AB.
Dễ thấy P, Q, R, S lần lượt là trung điểm của AE, BF, CH, DG.
Hình chữ nhật PQRS có \(PQ = \frac{1}{2} + 1 + \frac{1}{2} = 2,\,\,QK = \frac{{\sqrt 3 }}{2} \Rightarrow QR = \sqrt 3 \)
Quay hình chữ nhật PQRS quanh d ta được \({V_1} = \pi {\left( {\frac{{PQ}}{2}} \right)^2}QR = \pi {.1^2}.\sqrt 3 = \sqrt 3 \pi \)
Khi quay tam giác MEF quanh d ta được \({V_2} = \frac{1}{3}\pi .{\left( {\frac{1}{2}} \right)^2}.\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 \pi }}{{24}}\)
Tương tự khi quay tam giác NGH quanh d ta được khối tròn xoay có thể tích \({V_2}\)
Xét tam giác vuông API có: \(PI = \frac{{\sqrt 3 }}{2}\)
Khi quay tam giác API quanh d ta được \({V_3} = \frac{1}{3}\pi .A{P^2}.PI = \frac{1}{3}\pi {\left( {\frac{1}{2}} \right)^2}.\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 \pi }}{{24}}\)
Vậy khi xoay hình đã cho quanh d ta được vật tròn xoay có thể tích:
\(V = {V_1} + 2{V_2} + 4.\frac{{{V_3}}}{1} = \frac{{7\sqrt 3 \pi }}{6}\)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án B
Phương pháp:
Đồ thị hàm số \(y = \frac{{ax + b}}{{cx + d}}\left( {ad - bc \ne 0} \right)\) có TCN \(y = \frac{a}{c}\)
Cách giải:
\(y = 1 + \frac{{2x + 1}}{{x + 2}} = \frac{{3x + 3}}{{x + 2}}\) có TCN \(y = 3\)
Lời giải
Đáp án A
Phương pháp:
+) Tìm TXĐ của hàm số.
+) Tính đạo hàm của hàm số.
+) Giải bất phương trình \(y' > 0\) và suy ra các khoảng đồng biến của hàm số.
Cách giải:
TXĐ: \(D = \left( {0; + \infty } \right) \Rightarrow \) D đúng
Ta có: \(y' = \ln x + x.\frac{1}{x} = \ln x + 1 \Rightarrow \) C đúng
\(y' > 0 \Leftrightarrow \ln x > - 1 \Leftrightarrow x > {e^{ - 1}} = \frac{1}{e} \Rightarrow \) Hàm số đồng biến trên khoảng \(\left( {\frac{1}{e}; + \infty } \right) \Rightarrow \) B đúng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận