Câu hỏi:

27/02/2023 570

Xét các số thực dương x, y, z thỏa mãn x+y+z=4 và xy+yz+zx=5. Giá trị nhỏ nhất của biểu thức $(x^{3} + y^{3} + z^{3}) (\frac{1}{x} + \frac{1}{y} + \frac{1}{z})$ bằng

A. 20

B. 25

C. 15

D. 35

Xem lời giải

Câu hỏi trong đề: Bộ 20 đề thi giữa học kì 1 Toán 12 năm 2022-2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Chọn B

Ta có: $\{\begin{cases} x + y + z = 4 \\ x y + y z + z x = 5 \end{cases} \Leftrightarrow \{\begin{cases} x + y = 4 - z \\ x y = 5 - z (x + y) = 5 - 4 z + z^{2} \end{cases}$ .

Lại có: ${(x + y)}^{2} \geq 4 x y$ ${(x + y \Rightarrow {(4 - z)}^{2} \geq 4 (5 - 4 z + z^{2}) \Rightarrow \frac{2}{3} \leq z \leq 2)}^{2}$ . Dấu '=" xảy ra khi x=y.

Và ${(x + y + z)}^{3} = x^{3} + y^{3} + z^{3} + 3 (x + y + z) (x + y) z + 3 x y (x + y)$

$\Rightarrow x^{3} + y^{3} + z^{3} = 4^{3} - 12 (x + y) z - 3 x y (x + y) = 64 - 3 (4 - z) (5 + z^{2})$ .

Ta có: $P = (x^{3} + y^{3} + z^{3}) (\frac{1}{x} + \frac{1}{y} + \frac{1}{z}) = (3 z^{3} - 12 z^{2} + 15 z + 4) (\frac{5}{z^{3} - 4 z^{2} + 5 z})$ .

Đặt $t = z^{3} - 4 z^{2} + 5 z$ , với $\frac{2}{3} \leq z \leq 2 \Rightarrow \frac{50}{27} \leq t \leq 2$ .

Do đó xét hàm số $f (t) = 5 (\frac{4}{t} + 3)$ , với $\frac{50}{27} \leq t \leq 2$ .

Ta có $f^{'} (t) = \frac{- 20}{t^{2}} < 0, \forall t \in [\frac{50}{27}; 2]$ nên hàm số $f (t)$ liên tục và nghịch biến.

Do đó $P_{\min} = f (2) = 25$ đạt tại $x = y = 1$ , $z = 2$ .

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số f(x) có đạo hàm liên tục trên R và có đồ thị của hàm y=f'(x) như hình vẽ. Xét hàm số $g (x) = f (x^{2} - 2)$ . Mệnh đề nào dưới đây sai?

A. Hàm số

g (x)

đồng biến trên

(2; + \infty) .

B. Hàm số

g (x)

nghịch biến trên

(0; 2) .

C. Hàm số

g (x)

nghịch biến trên

(- 1; 0) .

D. Hàm số

g (x)

nghịch biến trên

(- \infty; - 2) .

Lời giải

Chọn C

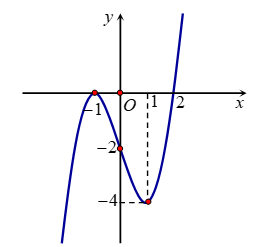
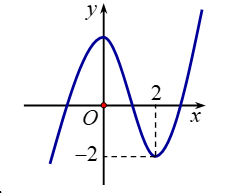
Dựa vào đồ thị hàm số $f^{'} (x) = 0 \Leftrightarrow [\begin{array}{l} x = - 1 \\ x = 2 \end{array}$ và $f^{'} (x) > 0 \Leftrightarrow x > 2$

Xét $g (x) = f (x^{2} - 2)$ có tập xác định R

$g' (x) = 2 x . f^{'} (t)$ với $t = x^{2} - 2$

$g' (x) = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ t = x^{2} - 2 = - 1 \\ t = x^{2} - 2 = 2 \end{array} \Leftrightarrow [\begin{array}{l} x = 0 \\ x = \pm 1 \\ x = \pm 2 \end{array}$

Lại có $f^{'} (t) > 0 \Leftrightarrow t = x^{2} - 2 > 2 \Leftrightarrow [\begin{array}{l} x > 2 \\ x < - 2 \end{array}$

Do đó, ta có bảng xét dấu $g^{'} (x)$

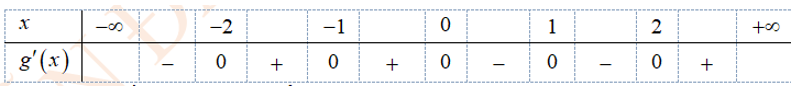
Cho hàm số f(x) có đạo hàm liên tục trên R và có đồ thị của hàm y=f'(x) như hình vẽ. Xét hàm số g(x)= f( x^2-2). Mệnh đề nào dưới đây sai? (ảnh 2)

Từ bảng xét dấu ta chọn phát biểu sai là C.

Câu 2

Cho hàm số y=f(x) liên tục trên R và có bảng xét dấu f'(x)như sau:

Hàm số y=f(x) có bao nhiêu điểm cực trị?

A. 1

B. 2

C. 3

D. 4

Lời giải

Chọn D

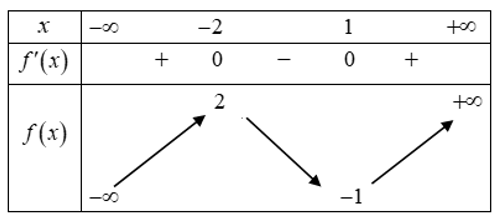
Hàm số f(x) liên tục trên R.

Từ bảng xét dấu ta thấy f'(x) đổi dấu khi qua $x = - 1, x = 0, x = 2, x = 4$ nên hàm số đã cho có 4 điểm cực trị.

Câu 3

Gọi I là giao điểm của hai đường tiệm cận của đồ thị hàm số $y = \frac{2 x - 3}{x + 1}$ . Khi đó, điểm I nằm trên đường thẳng có phương trình:

A. $x + y + 4 = 0$

B. $2 x - y + 4 = 0$

C. $x - y + 4 = 0$

D. $2 x - y + 2 = 0$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hàm số $y = f (x)$ có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?

A. Hàm số có giá trị cực tiểu bằng 2.

B. Hàm số đạt cực đại tại

x = 0

và đạt cực tiểu tại

x = 2

C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -2.

D. Hàm số có ba điểm cực trị.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một vật chuyển động theo quy luật $s = \frac{1}{3} t^{3} - t^{2} + 9 t,$ với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?

A. 89 $(m/s)$

B. 109 $(m/s)$

C. 71 $(m/s)$

D. $\frac{25}{3}$ $(m/s)$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho lăng trụ đứng ABCA'B'C'có đáy ABC là tam giác vuông tại A và AB=a $, A C = a \sqrt{3}$ mặt phẳng ( A'BC) tạo với mặt phẳng đáy ( ABC)một góc 30 $°$ . Tính thể tích khối lăng trụ ABCA'B'C'.

A. $\frac{a^{3}}{4}$

B. $\frac{a^{3} \sqrt{3}}{4}$

C. $\frac{a^{3}}{2}$

D. $\frac{a^{3} \sqrt{3}}{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hàm số y=f(x)có bảng biến thiên như sau:

Số nghiệm của phương trình $f (3 x^{4} - 6 x^{2} + 1) = 1$ là

A. 9

B. 10

C. 6

D. 8

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Xét các số thực dương x, y, z thỏa mãn x+y+z=4 và xy+yz+zx=5. Giá trị nhỏ nhất của biểu thức x3+y3+z31x+1y+1z bằng

Cho hàm số f(x) có đạo hàm liên tục trên R và có đồ thị của hàm y=f'(x) như hình vẽ. Xét hàm số g(x)=fx2−2. Mệnh đề nào dưới đây sai?

Cho hàm số y=f(x) liên tục trên R và có bảng xét dấu f'(x)như sau: Hàm số y=f(x) có bao nhiêu điểm cực trị?

Gọi I là giao điểm của hai đường tiệm cận của đồ thị hàm số y=2x−3x+1. Khi đó, điểm I nằm trên đường thẳng có phương trình:

Cho hàm số y=fx có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?

Cho lăng trụ đứng ABCA'B'C'có đáy ABC là tam giác vuông tại A và AB=a ,AC=a3mặt phẳng ( A'BC) tạo với mặt phẳng đáy ( ABC)một góc 30°. Tính thể tích khối lăng trụ ABCA'B'C'.

Cho hàm số y=f(x)có bảng biến thiên như sau: Số nghiệm của phương trình f3x4−6x2+1=1 là

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Xét các số thực dương x, y, z thỏa mãn x+y+z=4 và xy+yz+zx=5. Giá trị nhỏ nhất của biểu thức $(x^{3} + y^{3} + z^{3}) (\frac{1}{x} + \frac{1}{y} + \frac{1}{z})$ bằng

Cho hàm số f(x) có đạo hàm liên tục trên R và có đồ thị của hàm y=f'(x) như hình vẽ. Xét hàm số $g (x) = f (x^{2} - 2)$ . Mệnh đề nào dưới đây sai?

Cho hàm số y=f(x) liên tục trên R và có bảng xét dấu f'(x)như sau:

Hàm số y=f(x) có bao nhiêu điểm cực trị?

Gọi I là giao điểm của hai đường tiệm cận của đồ thị hàm số $y = \frac{2 x - 3}{x + 1}$ . Khi đó, điểm I nằm trên đường thẳng có phương trình:

Cho hàm số $y = f (x)$ có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?

Cho lăng trụ đứng ABCA'B'C'có đáy ABC là tam giác vuông tại A và AB=a $, A C = a \sqrt{3}$ mặt phẳng ( A'BC) tạo với mặt phẳng đáy ( ABC)một góc 30 $°$ . Tính thể tích khối lăng trụ ABCA'B'C'.

Cho hàm số y=f(x)có bảng biến thiên như sau:

Số nghiệm của phương trình $f (3 x^{4} - 6 x^{2} + 1) = 1$ là