Câu hỏi:
11/07/2024 1,816
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SAB và I là trung điểm của AB. Lấy điểm M trong đoạn AD sao cho AD = 3AM.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Đường thẳng qua M song song với AB cắt CI tại N.
Chứng minh rằng NG // (SCD).
c) Chứng minh rằng MG // (SCD).
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SAB và I là trung điểm của AB. Lấy điểm M trong đoạn AD sao cho AD = 3AM.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Đường thẳng qua M song song với AB cắt CI tại N.
Chứng minh rằng NG // (SCD).
c) Chứng minh rằng MG // (SCD).
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
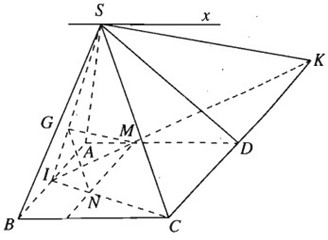
a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).
Ta có: \[\left\{ \begin{array}{l}AD \subset (SAD)\\BC \subset (SBC)\\AD\parallel BC\end{array} \right.\]
Do đó (SAD) ∩ (SBC) = Sx và Sx // AD // BC.
b) Ta có: MN // IA // CD
Suy ra \[\frac{{AM}}{{AD}} = \frac{{IN}}{{IC}} = \frac{1}{3}\].
Mà \[\frac{{IG}}{{IS}} = \frac{1}{3}\] (G là trọng tâm của ∆SAB) nên \[\frac{{IG}}{{IS}} = \frac{{IN}}{{IC}} = \frac{1}{3}\].
Ta có SC ⊂ (SCD) suy ra GN // (SCD).
c) Giả sử IM cắt CD tại K nên SK ⊂ (SCD).
MN // CD ⇒ \[\frac{{MN}}{{CK}} = \frac{{IN}}{{IC}} = \frac{1}{3}\] ⇒ \[\frac{{IM}}{{IK}} = \frac{1}{3}\].
Ta có: \[\left\{ \begin{array}{l}\frac{{IG}}{{IS}} = \frac{1}{3}\\\frac{{IM}}{{IK}} = \frac{1}{3}\end{array} \right.\] ⇒ GM // SK ⇒ GM // (SCD).Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới)
Đã bán 1,5k
₫ 70.000
₫ 36.000
Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn)
Đã bán 1,4k
₫ 280.000
₫ 150.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tìm m để hàm số y = x3 − 3(2m + 1)x2 + (12m + 5)x + 2 đồng biến trên khoảng (2; +∞).
Xem đáp án »
02/04/2025
17,747
Câu 3:
Tìm các tham số a, b, c sao cho hàm số y = ax2 + bx + c đạt GTNN là 4 tại x = 2 và đồ thị hàm số của nó cắt trục tung tại điểm có tung độ là 6.
Xem đáp án »
13/07/2024
14,803
Câu 4:
Tính chu vi và diện tích một hình tam giác vuông có một cạnh góc vuông dài 24 cm và bằng \(\frac{3}{4}\) cạnh góc vuông kia. Cạnh còn lại dài 40 cm.
Xem đáp án »
13/07/2024
12,387
Câu 5:
Cho a,b,c là các số thực dương thỏa mãn a + b + c = 1. Chứng minh rằng:
\(\frac{{a + bc}}{{b + c}} + \frac{{b + ca}}{{c + a}} + \frac{{c + ab}}{{a + b}} \ge 2\).
Cho a,b,c là các số thực dương thỏa mãn a + b + c = 1. Chứng minh rằng:
\(\frac{{a + bc}}{{b + c}} + \frac{{b + ca}}{{c + a}} + \frac{{c + ab}}{{a + b}} \ge 2\).
Xem đáp án »
13/07/2024
12,206
Câu 6:
Cho bất phương trình: (m − 2)x2 + 2(4 − 3m)x + 10m − 11 ≤ 0 (1). Gọi S là tập hợp các số nguyên dương m để bất phương trình đúng với mọi x < −4. Tìm số phần tử của S.
Xem đáp án »
13/07/2024
9,737
Câu 7:
Tìm điều kiện của tham số để đồ thị hàm số y = (m − 2)x + m tạo với trục Ox một góc nhọn, góc tù.
Xem đáp án »
13/07/2024
7,995
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
-
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận