Câu hỏi:
13/07/2024 1,974
Cho tam giác ABC vuông tại A. Biết AB = 12 cm, AC = 16 cm, đường phân giác AD, đường cao AH . Tính HD, HB.
Câu hỏi trong đề:
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
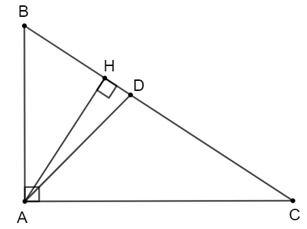
Ta có: BC2 = AB2 + AC2
= 122 + 162 = 400
⇒ BC = \[\sqrt {400} \] = 20 (cm)
Δ ABC vuông có đường cao AH:
⇒ AB2 = BH.BC
⇒ BH = \[\frac{{A{B^2}}}{{BC}}\] = \[\frac{{{{12}^2}}}{{20}}\] = 7,2 (cm)
⇒ CH = 20 – 7,2 = 12,8 (cm)
Ta có: AD là phân giác
⇒ \[\frac{{BD}}{{CD}}\] = \[\frac{{AB}}{{AC}}\]
⇒ \[\frac{{BD + CD}}{{CD}}\] = \[\frac{{AB + AC}}{{AC}}\]
⇒ \[\frac{{20}}{{CD}}\] = \[\frac{{28}}{{16}}\]
⇒ CD = \[\frac{{80}}{7}\]
⇒ HD = CH – CD
= 12,8 – \[\frac{{80}}{7}\] = \[\frac{{48}}{{35}}\] (cm).
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tìm m để hàm số y = x3 − 3(2m + 1)x2 + (12m + 5)x + 2 đồng biến trên khoảng (2; +∞).
Xem đáp án »
13/07/2024
14,669
Câu 3:
Tìm các tham số a, b, c sao cho hàm số y = ax2 + bx + c đạt GTNN là 4 tại x = 2 và đồ thị hàm số của nó cắt trục tung tại điểm có tung độ là 6.
Xem đáp án »
13/07/2024
10,325
Câu 4:
Tính chu vi và diện tích một hình tam giác vuông có một cạnh góc vuông dài 24 cm và bằng \(\frac{3}{4}\) cạnh góc vuông kia. Cạnh còn lại dài 40 cm.
Xem đáp án »
13/07/2024
8,518
Câu 5:
Cho bất phương trình: (m − 2)x2 + 2(4 − 3m)x + 10m − 11 ≤ 0 (1). Gọi S là tập hợp các số nguyên dương m để bất phương trình đúng với mọi x < −4. Tìm số phần tử của S.
Xem đáp án »
13/07/2024
7,257
Câu 6:
Cho a,b,c là các số thực dương thỏa mãn a + b + c = 1. Chứng minh rằng:
\(\frac{{a + bc}}{{b + c}} + \frac{{b + ca}}{{c + a}} + \frac{{c + ab}}{{a + b}} \ge 2\).
Cho a,b,c là các số thực dương thỏa mãn a + b + c = 1. Chứng minh rằng:
\(\frac{{a + bc}}{{b + c}} + \frac{{b + ca}}{{c + a}} + \frac{{c + ab}}{{a + b}} \ge 2\).
Xem đáp án »
13/07/2024
6,601
Câu 7:
Cho tam giác ABC vuông tại A, điểm M bất kỳ trên cạnh BC. Gọi D, E theo thứ tự là chân đường vuông góc kẻ từ M đến AB và AC. Tứ giác ADME là hình gì?
Xem đáp án »
13/07/2024
5,014
về câu hỏi!