Câu hỏi:

13/07/2024 3,855

Cho hàm số y = (2m – 3).x + m – 5. Tìm m để đồ thị hàm số:

a) tạo với 2 trục tọa độ một tam giác vuông cân

b) cắt đường thẳng y = 3x – 4 tại một điểm trên Oy

c) cắt đường thẳng y = – x – 3 tại một điểm trên Ox.

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải

a) Gọi giao điểm của đồ thị hàm số với trục Ox là A

Suy ra \(A\left( {\frac{{5 - m}}{{2m - 3}};0} \right)\) nên OA = \(\left| {\frac{{5 - m}}{{2m - 3}}} \right|\); (m ≠ \(\frac{3}{2}\))

Gọi giao điểm của đồ thị hàm số với trục Oy là B

Suy ra B(0; m – 5) nên OB = \(\left| {m - 5} \right|\)

Ta có tam giác AOB vuông tại O.

Để tam giác AOB vuông cân tại O thì OA = OB

Hay \(\left| {\frac{{5 - m}}{{2m - 3}}} \right|\) = \(\left| {m - 5} \right|\)

\( \Rightarrow \left[ \begin{array}{l}\frac{{5 - m}}{{2m - 3}} = m - 5\\\frac{{5 - m}}{{2m - 3}} = 5 - m\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2m - 3 = - 1\\2m - 3 = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2m = 2\\2m = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = 2\end{array} \right.\) (thỏa mãn)

Vậy m = 1 hoặc m = 2 thì đồ thị hàm số tạo với 2 trục tọa độ một tam giác vuông cân

b) Đồ thị hàm số cắt đường thẳng y = 3x – 4 tại một điểm trên Oy

Suy ra giao điểm B(0; m – 5) của đồ thị hàm số đã cho và Oy thuộc đường thẳng y = 3x – 4

Nên m – 5 = 3.0 – 4

Hay m = 1

Vậy m = 1 thì đồ thị hàm số cắt đường thẳng y = 3x – 4 tại một điểm trên Oy

c) Đồ thị hàm số cắt đường thẳng y = – x – 3 tại một điểm trên Ox

Suy ra giao điểm \(A\left( {\frac{{5 - m}}{{2m - 3}};0} \right)\) của đồ thị hàm số đã cho và Ox thuộc đường thẳng \[y = --x--3\]

Nên \( - \frac{{5 - m}}{{2m - 3}} - 3 = 0\)

⇔ m – 5 = 3.(2m – 3)

⇔ m – 5 = 6m – 9

⇔ – 5m = – 4

\( \Leftrightarrow m = \frac{4}{5}\)

Vậy \(m = \frac{4}{5}\) thì đồ thị hàm số cắt đường thẳng y = – x – 3 tại một điểm trên Ox.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh:

a) AB² = BH . BC;

b) AH² = BH . HC;

c) AB . AC = AH . BC;

d) AC² = CH . BC.

Xem đáp án

Lời giải

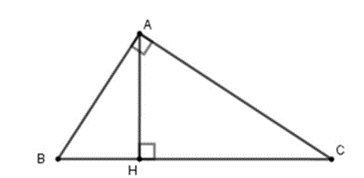
Media VietJack

a) Xét ∆ABH và ∆CBA có:

\(\widehat {BHA} = \widehat {BAC} = 90^\circ \)

\(\widehat {ABC}\) chung.

Do đó (g.g)

Suy ra \(\frac{{AB}}{{CB}} = \frac{{BH}}{{BA}}\) (tỉ số đồng dạng)

Do đó AB² = BH . BC.

b) Vì tam giác AHC vuông tại H nên \(\widehat {HCA} + \widehat {HAC} = 90^\circ \)(trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Mà \(\widehat {BAH} + \widehat {HAC} = \widehat {BAC} = 90^\circ \)

Suy ra \(\widehat {BAH} = \widehat {HCA}\)

Xét ∆AHB và ∆CHA có:

\(\widehat {BHA} = \widehat {AHC} = 90^\circ \)

\(\widehat {BAH} = \widehat {HCA}\)(chứng minh trên)

Do đó (g.g)

Suy ra \(\frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\) (tỉ số đồng dạng)

Do đó AH² = BH . CH.

c) Ta có \[{S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}AH.BC\]

Suy ra AB . AC = AH . BC.

d) Xét ∆CAH và ∆CBA có:

\(\widehat {CHA} = \widehat {BAC} = 90^\circ \).

\(\widehat {ACB}\) chung.

Do đó (g.g)

Suy ra \(\frac{{AC}}{{BC}} = \frac{{HC}}{{AC}}\) (tỉ số đồng dạng)

Do đó AC² = CH . BC.

Câu 2

Cho 5 điểm A, B, C, D, E. Chứng minh rằng:

a) \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EA} \) = \(\overrightarrow {CB} + \overrightarrow {ED} \).

b) \(\overrightarrow {AC} + \overrightarrow {CD} - \overrightarrow {EC} \) = \(\overrightarrow {A{\rm{E}}} - \overrightarrow {BD} + \overrightarrow {CB} \).

Xem đáp án

Lời giải

a) Ta có:

\(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EA} \)

= \(\overrightarrow {EA} + \overrightarrow {AB} + \overrightarrow {CD} \)

= \(\overrightarrow {EB} + \overrightarrow {CD} \)

= \(\overrightarrow {ED} + \overrightarrow {DB} + \overrightarrow {CB} + \overrightarrow {BD} \)

= \(\overrightarrow {ED} + \overrightarrow {CB} + (\overrightarrow {BD} + \overrightarrow {DB} )\)

= \(\overrightarrow {CB} + \overrightarrow {ED} \)

Vậy \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EA} \) = \(\overrightarrow {CB} + \overrightarrow {ED} \)

b) Ta có:

\(\overrightarrow {AC} + \overrightarrow {CD} - \overrightarrow {EC} \)

= \(\overrightarrow {AC} + \overrightarrow {CD} + \overrightarrow {CE} \)

= \(\overrightarrow {AC} + \overrightarrow {CE} + \overrightarrow {CD} \)

= \(\overrightarrow {AE} + \overrightarrow {CD} \)

= \(\overrightarrow {AE} + \overrightarrow {CB} + \overrightarrow {BD} \)

= \(\overrightarrow {A{\rm{E}}} - \overrightarrow {BD} + \overrightarrow {CB} \)

Vậy \(\overrightarrow {AC} + \overrightarrow {CD} - \overrightarrow {EC} \) = \(\overrightarrow {A{\rm{E}}} - \overrightarrow {BD} + \overrightarrow {CB} \).

Câu 3